面板数据模型形式的选择,经典面板数据模型的一般形式

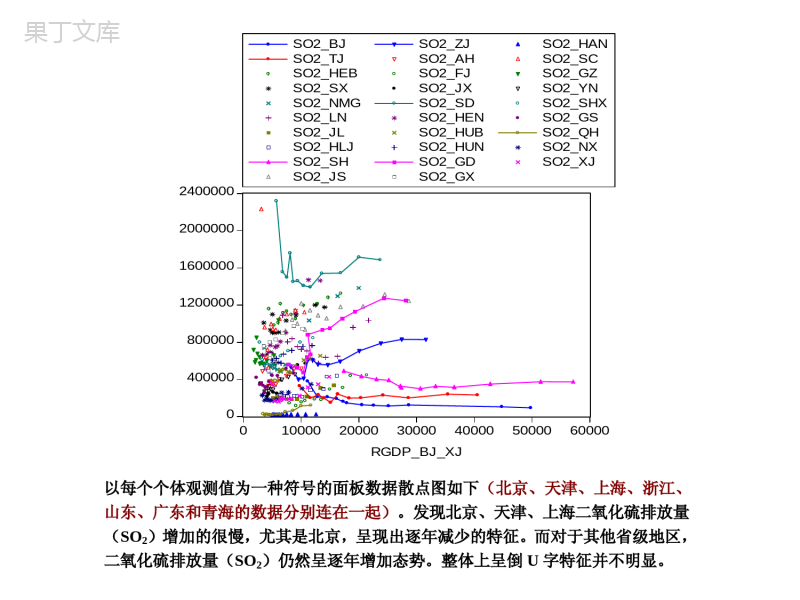
面板数据模型形式的选择张晓峒南开大学数量经济研究所nkeviews@yahoo.com.cn面板数据模型形式的选择张晓峒【摘要】面板数据模型除了应用F检验和Hausman检验确定应该建立混合模型、固定效应模型还是随机效应模型之外，如何恰当地选择模型的形式也是一个重要问题。本文运用多组经济数据展示模型形式的选择过程以及模型形式不合理时对模型参数估计带来的影响。案例1：工业SO2排放及人均GDP关系的面板数据研究以中国29个省级地区（不包括重庆、西藏和港澳台地区）1995-2006年间12年的面板数据来对我国的经济增长与环境问题做出分析，所选数据均为平衡面板数据，共348组数据。其中，RGDP表示人均国内生产总值（单位：元），SO2表示工业二氧化硫排放量（单位：吨）。用BJ、TJ、HEB、SX、NMG、LN、JL、HLJ、SH、JS、ZJ、AH、FJ、JX、SD、HEN、HUB、HUN、GD、GX、HAN、SC、GZ、YN、SHX、GS、QH、NX、XJ分别表示北京、天津、河北、山西、内蒙古、辽宁、吉林、黑龙江、上海、江苏、浙江、安徽、福建、江西、山东、河南、湖北、湖南、广东、广西、海南、四川、贵州、云南、陕西、甘肃、青海、宁夏、新疆。各地区1995-2006的人均国内生产总值和工业二氧化硫排放量数据均来自于1996-2007年《中国统计年鉴》。案例1：工业SO2排放及人均GDP关系的面板数据研究线性混合模型估计结果是SO2it=557081.4+1.1111RGDPit（16.0）（0.4）R2=0.0005，DW=0.11,NT=2912=348说明二氧化硫排放量（SO2it,吨）与人均国内生产总值（RGDPit,元）之间不存在线性关系。由可决系数R2=0.0005知数据一定非常散。二次多项式混合模型估计结果是SO2it=423499.3+23.4691RGDPit-0.00055RGDPit2（8.0）（3.2）（-3.3）R2=0.0315，DW=0.12,NT=2912=348说明二氧化硫排放量（SO2it）与人均国内生产总值（RGDPit）有可能存在二次非线性关系。由可决系数R2=0.0315知数据一定非常散。据此就可以建立二次多项式形式的面板数据模型吗？首先分析数据散点图。案例1：工业SO2排放及人均GDP关系的面板数据研究040000080000012000001600000200000024000000100002000030000400005000060000RGDPSO2_95SO2_96SO2_97SO2_98SO2_99SO2_00SO2_01SO2_02SO2_03SO2_04SO2_05SO2_06二氧化硫排放量（SO2it）与人均国内生产总值（RGDPit）面板数据散点图。案例1：工业SO2排放及人均GDP关系的面板数据研究040000080000012000001600000200000024000000100002000030000400005000060000RGDPSO2_95_06SO2_95_06F1-500000050000010000001500000200000025000000100002000030000400005000060000RGDPSO2_95_06SO2_95_06vs.Polynomial(degree=2)ofRGDP线性混合模型的回归直线二次多项式回归曲线拟合二次回归曲线是没有道理的（人均国内生产总值超过6万元之后，二氧化硫排放量（SO2）为负）。那么应该建立何种面板数据模型呢？案例1：工业SO2排放及人均GDP关系的面板数据研究经济理论中有反映经济增长与收入分配之间关系的库兹涅茨曲线(Kuznets，1955)（人均国民收入从最低上升到中等水平时，收入分配状况先趋于恶化，继而随着经济发展，逐步改善，最后达到比较公平的收入分配状况，呈颠倒过来的U的形状）GrossmanandKrueger(1991)在分析环境效应时,通过对42个国家截面数据的分析，研究了SO2、微尘和悬浮颗粒三种环境质量指标与收入之间的关系，发现环境污染与经济增长的长期关系呈倒U形，并且判断出在一国人均GDP未达到4000-5000美元的转折点时，经济增长趋向于加重环境压力；一旦一国人均GDP超过了4000-5000美元的转折点，经济增长就开始倾向于减轻环境压力。1000002000003000004000005000006000007000008000000100002000030000400005000060000so2rgdp案例1：工业SO2排放及人均GDP关系的面板数据研究GrossmanandKrueger(1991)用人均收入变化的三类效应来解释该现象的出现:经济发展意味着更大规模的经济活动与资源需求量,因而对环境产生负面的规模效应；但同时经济发展又通过正的技术进步效应(例如更为环保的新技术的使用)以及结构效应(例如产业结构的升级与优化)减少了污染排放、改善了环境质量。因此,这三类效应共同决定了环境质量与经济发展之间的这一倒U型曲线关系。案例1：工业SO2排放及人均GDP关系的面板数据研究分析中国二氧化硫排放量（SO2）与人均国内生产总值（RGDP）面板数据的特征。040000080000012000001600000200000024000000100002000030000400005000060000RGDPSO2_95SO2_96SO2_97SO2_98SO2_99SO2_00SO2_01SO2_02SO2_03SO2_04SO2_05SO2_06以每个截面观测值为一种符号的面板数据散点图如下（图中把1995、2001和2006年数据分别连在一起。）：发现二氧化硫排放量（SO2）有逐年增加的趋势。040000080000012000001600000200000024000000100002000030000400005000060000RGDP_BJ_XJSO2_BJSO2_TJSO2_HEBSO2_SXSO2_NMGSO2_LNSO2_JLSO2_HLJSO2_SHSO2_JSSO2_ZJSO2_AHSO2_FJSO2_JXSO2_SDSO2_HENSO2_HUBSO2_HUNSO2_GDSO2_GXSO2_HANSO2_SCSO2_GZSO2_YNSO2_SHXSO2_GSSO2_QHSO2_NXSO2_XJ以每个个体观测值为一种符号的面板数据散点图如下（北京、天津、上海、浙江、山东、广东和青海的数据分别连在一起）。发现北京、天津、上海二氧化硫排放量（SO2）增加的很慢，尤其是北京，呈现出逐年减少的特征。而对于其他省级地区，二氧化硫排放量（SO2）仍然呈逐年增加态势。整体上呈倒U字特征并不明显。案例1：工业SO2排放及人均GDP关系的面板数据研究040000080000012000001600000200000024000000100002000030000400005000060000RGDPSO2_95_06SO2_95_06vs.Polynomial(degree=3)ofRGDP面板数据的三次多项式混合模型拟合图（按库兹涅茨曲线假说拟合）。估计结果显示这种拟合没有显著性，即不存在倒U字特征。SO2it=349806.2+41.5645RGDPit-0.00156RGDPit2+1.38108RGDPit2（4.3）（2.4）（-1.8）（1.2）R2=0.035，DW=0.12,NT=2912=348040000080000012000001600000200000024000000100002000030000400005000060000RGDP_BJ_XJSO2_BJSO2_TJSO2_HEBSO2_SXSO2_NMGSO2_LNSO2_JLSO2_HLJSO2_SHSO2_JSSO2_ZJSO2_AHSO2_FJSO2_JXSO2_SDSO2_HENSO2_HUBSO2_HUNSO2_GDSO2_GXSO2_HANSO2_SCSO2_GZSO2_YNSO2_SHXSO2_GSSO2_QHSO2_NXSO2_XJ从面板数据个体连线散点图看，人均国内生产总值超过4万元的只有北京、天津、上海三个地区。其余26个省级地区仍都处于二氧化硫排放量（SO2）逐年增加的阶段。用倒U字曲线拟合是不恰当的。案例1：工业SO2排放及人均GDP关系的面板数据研究回到线性拟合形式上来。与混合模型SO2it=557081.4+1.1111RGDPit（16.0）（0.4）R2=0.0005，DW=0.11,NT=2912=348相对应，估计个体固定效应模型如下：SO2it=…+461948.1+10.5148RGDPit（24.2）（5.2）R2=0.86，DW=0.79,NT=2912=348从全国平均水平来看，人均国内生产总值（RGDP）每增加1元，二氧化硫排放量（SO2）增加10.5吨。从检验结果看应该建立个体固定效应模型。案例1：工业SO2排放及人均GDP关系的面板数据研究相对应，估计随机效应模型如下：SO2it=…+465399.6+10.1736RGDPit（6.4）（6.1）R2=0.10，DW=0.72,NT=2912=348从检验结果看应该建立个体随机效应模型。如果建立二次多项式模型，预测将带来很大误差。本例不应建立倒U字模型，中国目前处于工业化发展阶段，还没有逾越二氧化硫排放量的最高值。案例2：全国省级地区城镇居民人均食品支出与收入关系研究28个省市自治区（不包括西藏、新疆和重庆市）21年（19852005）共588个观测值。线性混合模型估计结果是F1it=335.84+0.2667I1it（20.6）（88.8）R2=0.93，DW=0.15,NT=2821=588线性个体固定效应模型估计结果是F1it=…+374.75+0.2577I1it（26.6）（96.8）R2=0.95，DW=0.23,NT=2821=588克服误差项自相关的线性个体固定效应模型估计结果是F1it=…+604.98+0.2225I1it+1.1979AR(1)-0.3620AR(2)（11.8）（34.1）（28.5）（-8.8）R2=0.99，DW=2.24,NT=2821=532R2=0.99，DW=2.24，一定认为找到了模型的最好估计形式。事实并不是这样。F1it和I1it的散点图如下：案例2：全国省级地区城镇居民人均食品支出与收入关系研究010002000300040005000040008000120001600020000incomefood散点图显示，变量food和income之间存在非线性关系和异方差，建立线性模型不合理。经观测，对数模型、倒数模型都不合理。-1000010002000300040005000040008000120001600020000I1F1F1vs.LogI1-2000-1000010002000300040005000040008000120001600020000I1F1F1vs.InverseofI1案例2：全国省级地区城镇居民人均食品支出与收入关系研究010002000300040005000040008000120001600020000I1F1F1vs.Polynomial(degree=2)ofI15.56.06.57.07.58.08.59.06.06.57.07.58.08.59.09.510.0LOG(I1)LOG(F1)LOG(F1)vs.LOG(I1)2次多项式模型拟合的合理，但未克服异方差。对数线性模型拟合的较合理，但从散点图看对数变量仍属于非线性模型。案例2：全国省级地区城镇居民人均食品支出与收入关系研究5.56.06.57.07.58.08.59.06.06.57.07.58.08.59.09.510.0LOG(CINCOME)LOG(Cfood)5.56.06.57.07.58.08.59.01.801.851.901.952.002.052.102.152.202.252.30LOG(LOG(I1))LOG(F1)log(Food)和log(income)的混合数据散点图log(Food)和log(log(income))的散点图如右图，应该建立关于log(Food)和log(log(income))的线性面板数据模型。案例2：全国省级地区城镇居民人均食品支出与收入关系研究首先用混合数据（非面板数据）估计模型。得回归结果如下，logfood=-5.8117+6.2072log(logincome)（-61.7）（137.3）R2=0.97，DW=2.0,NT=588样本容量应该是NT=2131=651，但西藏、新疆、重庆的数据有缺失。F检验结果显示混合模型与个体固定效应模型相比较，应该建立个体固定效应模型。案例2：全国省级地区城镇居民人均食品支出与收入关系研究Hausman检验结果显示个体随机效应模型与个体固定效应模型相比较，应该建立个体固定效应模型。建立带有两个误差自回归项的个体固定效应模型如下：logfood=-4.9784+…+5.8147log(logincome)+1.0093AR(1)-0.3349AR(2)（-34.9）（86.4）（24.7）（-8.4）R2=0.995，DW=2.2,NT=532案例2：全国省级地区城镇居民人均食品支出与收入关系研究建立带有两个误差自回归项的个体固定效应模型如下：logfood=-4.9784+…+5.8147log(logincome)+1.0093AR(1)-0.3349AR(2)（-34.9）（86.4）（24.7）（-8.4）R2=0.995，DW=2.2,NT=532上式两侧求导，tttttincomedincomeincomelogfooddfood18147.5。弹性函数是tttttincomelogincomedincomefooddfood18147.5。上式说明城镇人均食品支出对人均收入的弹性系数随着人均收入的提高而递减。经计算，当人均收入为1000元时，人均食品支出对人均收入的弹性系数是0.84。当城镇人均收入增长到15000元时，人均食品支出对人均收入的弹性系数下降到0.60。如果认为该弹性系数是常量，即建立对数线性模型是不妥的。案例2：全国省级地区城镇居民人均食品支出与收入关系研究安徽省和北京市城镇人均食品支出的静态预测结果。05001,0001,5002,0002,5003,00086889092949698000204F1ANHF1ANH(Baseline)01,0002,0003,0004,0005,00086889092949698000204F1BEJF1BEJ(Baseline)案例3：实物资本、人力资本对人均GDP的贡献是多少？在宏观经济学的新增长理论中，经济学家提出人力资本这一概念，将其加入到生产函数中，以此试图解释收入的地区差异。但是实物资本和人力资本在生产函数中究竟各起到什么样的作用呢?设y为人均产出，k为人均实物资本，edu是人均受教育年数。假设每个人的人力资本量仅取决于他所接受的教育年数edu。显然，人们接受教育越多，其人力资本就越多。案例3：实物资本、人力资本对人均GDP的贡献是多少？我们将以中国29个省级地区（不包括重庆、西藏和港澳台地区）1987-2001年间15年的面板数据来对我国的生产函数进行分析，其中宁夏缺少1987-1989年的三组数据，所以一共有432组数据。y表示人均国内生产总值（单位：元），k表示人均资本形成总额（单位：元），edu表示人均受教育的时间（单位：年）。用BJ、TJ、HEB、SXC、NMG、LN、JL、HLJ、SH、JS、ZJ、AH、FJ、JX、SD、HEN、HUB、HUN、GD、GX、HN、SC、GZ、YN、SX、GS、QH、NX、XJ分别表示北京、天津、河北、山西、内蒙古、辽宁、吉林、黑龙江、上海、江苏、浙江、安徽、福建、江西、山东、河南、湖北、湖南、广东、广西、海南、四川、贵州、云南、陕西、甘肃、青海、宁夏和新疆。案例3：实物资本、人力资本对人均GDP的贡献是多少？线性混合模型估计结果如下:itititeduky01.3178711.12.1402ˆ(-2.8)(51.6)(3.9)R2=0.937，DW=0.26,NT=432R2=0.937，也许认为得到了一个非常好的估计结果。实际并不是。案例3：实物资本、人力资本对人均GDP的贡献是多少？05,00010,00015,00020,00025,00030,00035,00040,00002,5005,0007,50010,00012,50015,000YBJYTJYHEBYSXCYNMGYLNYJLYHLJYSHYJSYZJYAHYFJYJXYSDYHENYHUBYHUNYGDYGXYHNYSCYGZYYNYSXYGSYQHYNXYXJK分析数据表现。29个地区15年人均产出yit对人均物质资本kit面板数据散点图如下（人均受教育时间是平衡面板数据，但人均产出和人均资本存量不是平衡面板数据）：数据存在异方差。案例3：实物资本、人力资本对人均GDP的贡献是多少？05,00010,00015,00020,00025,00030,00035,00040,0004567891011YAHYBJYFJYGDYGSYGXYGZYHEBYHENYHLJYHNYHUBYHUNYJLYJSYJXYLNYNMGYNXYQHYSCYSDYSHYSXYSXCYTJYXJYYNYZJEDU人均产出yit对人均教育时间eduit的面板数据散点图存在异方差，且关系为指数形式（不是线性的）。案例3：实物资本、人力资本对人均GDP的贡献是多少？取对数后人均产出lnyit与人均物质资本lnkit的线性关系十分明显。不再存在异方差。678910115.05.56.06.57.07.58.08.59.09.510.0LNYAH01LNYBJ01LNYGD01LNYGS01LNYGX01LNYGZ01LNYHEB01LNYHEN01LNYHLJ01LNYHN01LNYHUB01LNYHUN01LNYJL01LNYJS01LNYJX01LNYLN01LNYNMG01LNYNX01LNYQH01LNYSC01LNYSD01LNYSH01LNYSXC01LNYTJ01LNYXJ01LNYYN01LNYZJ01LOG(K)对数形式的人均产出lnyit与人均受教育时间eduit存在线性关系。678910114567891011LNYAH01LNYBJ01LNYGD01LNYGS01LNYGX01LNYGZ01LNYHEB01LNYHEN01LNYHLJ01LNYHN01LNYHUB01LNYHUN01LNYJL01LNYJS01LNYJX01LNYLN01LNYNMG01LNYNX01LNYQH01LNYSC01LNYSD01LNYSH01LNYSXC01LNYTJ01LNYXJ01LNYYN01LNYZJ01EDU案例3：实物资本、人力资本对人均GDP的贡献是多少？结合图形分析，建立如下非线性计量模型：itititititueduLnkcLny混合回归模型估计结果：itititeduLnkLny0835.08113.06672.1(26.5)(58.5)(6.84)R2=0.96，DW=0.38,NT=432个体固定效应模型估计结果：itititeduLnkLny2062.07633.01887.1(21.7)(48.8)(11.3)R2=0.985，DW=1.1,NT=432案例3：实物资本、人力资本对人均GDP的贡献是多少？再建立个体固定效应回归模型，估计结果如下：Lnyit=…+0.76Lnkit+0.21eduit+uit(48.8)(11.3)R2=0.98,SSE=4.4,DW=1.06模型DW值太小，可能存在自相关。加入AR(1)后的个体固定效应回归模型估计结果如下：Lnyit=…+0.75Lnkit+0.16eduit+0.58AR(1)+vit(34.5)(7.9)(12.5)R2=0.99,SSE=3.2,DW=2.09已消除自相关。案例3：实物资本、人力资本对人均GDP的贡献是多少？F检验结果：F=24.7>F0.05(28,401)，推翻原假设。个体固定效应回归模型比混合回归模型合理。Hausman检验的原假设和备择假设分别为：H0：个体随机效应回归模型。H1：个体固定效应回归模型因为H=22.4>20.05(2)=6.0，结论是，模型存在个体固定效应，应该建立个体固定效应回归模型。案例3：实物资本、人力资本对人均GDP的贡献是多少？Lnyit=…+0.75Lnkit+0.16eduit+0.58AR(1)+vit(34.5)(7.9)(12.5)R2=0.99,SSE=3.2,DW=2.09经济含义是，人均产出yit对人均资本kit的弹性系数是0.75。人均资本每增加1%，人均产出增加0.75%。人均产出Lnyit对人均受教育时间eduit的弹性系数是itititititeduedudeduydy16.0人均受教育时间每增加1年，人均产出yit增加16%。弹性系数是0.16eduit。随着受教育年限的增加，产出越来越大。谢谢