中考专题--半角模型,半角模型中考真题

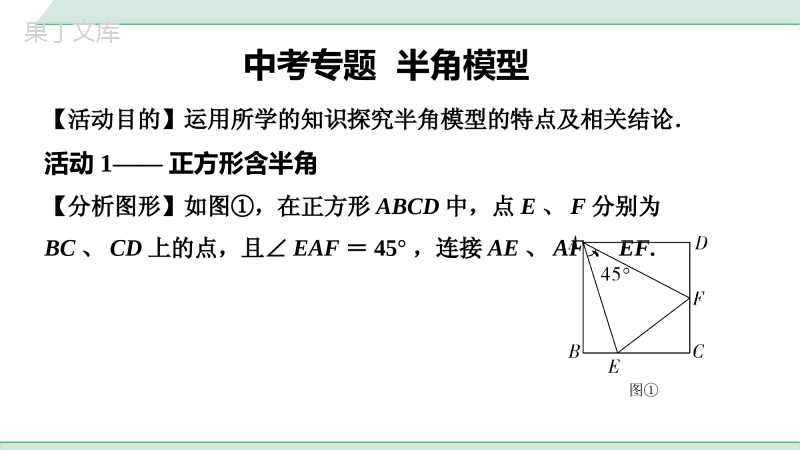
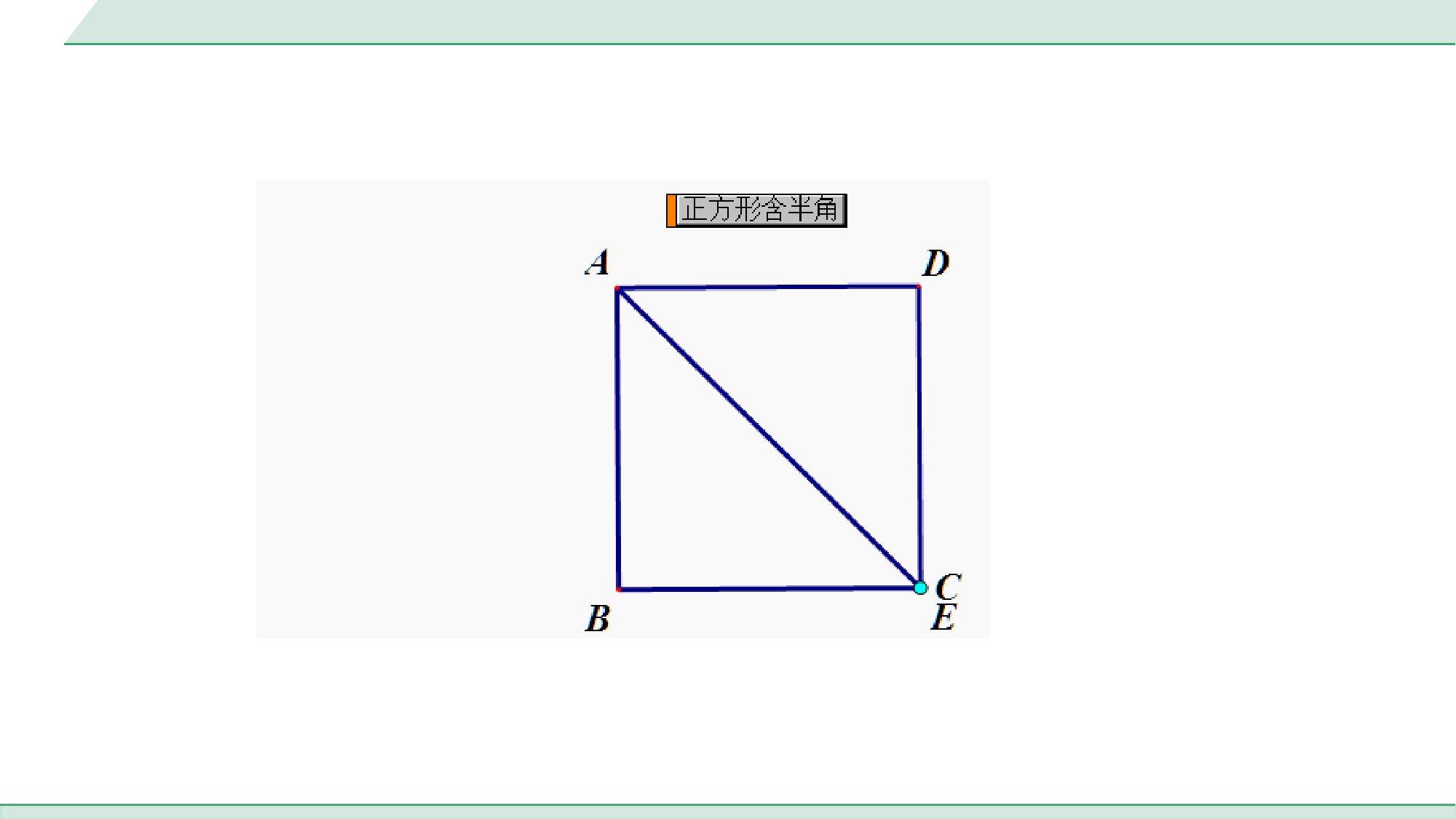
满分技法【活动目的】运用所学的知识探究半角模型的特点及相关结论．活动1——正方形含半角【分析图形】如图①，在正方形ABCD中，点E、F分别为BC、CD上的点，且∠EAF＝45°，连接AE、AF、EF.图①中考专题半角模型【提出问题】请证明以下结论是否成立：EF＝BE＋DF.【解决问题】【方法一】补短法图①证明：如解图①，延长CD至点G，使得DG＝BE，G∵四边形ABCD是正方形，∴AB＝AD，∠ABE＝∠ADG＝90°，在△ABE和△ADG中，∴△ABE≌△ADG(SAS)，,ABADABEADGBEDG,ABADABEADGBEDG∴∠BAE＝∠DAG，AE＝AG，∵∠EAF＝45°，∠BAD＝90°，∴∠BAE＋∠FAD＝45°，∴∠DAG＋∠FAD＝45°，即∠GAF＝45°，∴∠EAF＝∠GAF，在△AFE和△AFG中，∴△AFE≌△AFG(SAS)，∴EF＝GF＝DG＋DF＝BE＋DF.,AEAFEAFGAFAEAGG图①,AEAFEAFGAFAEAG满分技法补短法的辅助线作法：找出相等的两条线段所在的两个直角三角形，延长其中一个直角三角形较短的直角边，使其等于另一个直角三角形较短的直角边的长度，连接公共端点与延长后的端点．【方法二】旋转法图①证明：如解图②，将△ADF绕点A顺时针旋转90°得到△ABG，使AD与AB重合，由旋转的性质可知，△ADF≌△ABG，∴DF＝BG，AF＝AG，∴∠GAB＝∠FAD，∵∠EAF＝45°，∠BAD＝90°，∴∠BAE＋∠FAD＝45°，∴∠BAE＋∠GAB＝45°，即∠EAG＝45°，G∴在△AFE和△AGE中，∴△AFE≌△AGE(SAS)，∴EF＝EG，∵EG＝BG＋BE，∴EF＝BE＋DF.,AFAGEAFEAGAEAEG图①,AFAGEAFEAGAEAE满分技法旋转法的辅助线作法：以公共端点为旋转中心，相等的两条线段的夹角为旋转角，旋转某一直角三角形，使相等的两直角边重合．活动2——等腰直角三角形含半角【类比探究】如图②，在Rt△BAC中，AB＝AC，∠BAC＝90°，点D、E在BC边上，且∠DAE＝45°.图②【提出问题】请证明以下结论是否成立：①DE2＝BD2＋CE2；②△ABE∽△DAE∽△DCA.【解决问题】【方法一】旋转法图②证明：如解图③，将△ABD绕点A逆时针旋转得到△ACF，使AB与AC重合，连接EF，根据旋转的性质可得，△BAD≌△CAF，∴∠BAD＝∠CAF，AD＝AF，CF＝BD，F∵∠BAC＝90°，∠DAE＝45°，∴∠DAE＝∠EAF＝45°，在△AEF和△AED中，∴△AEF≌△AED(SAS)，∴EF＝ED，∵AB＝AC，∴∠ABC＝∠ACB＝∠ACF＝45°，∴∠ECF＝90°，,AFADEAFEADAEAE图②F,AFADEAFEADAEAE在Rt△ECF中，根据勾股定理可得，EF2＝EC2＋CF2，∴DE2＝BD2＋EC2，∴结论①成立；∵∠B＝∠ACB＝∠DAE＝45°，∠AEB＝∠ACB＋∠CAE＝45°＋∠CAE，∵∠CAD＝∠DAE＋∠CAE＝45°＋∠CAE，图②F则△ABE∽△DCA.∵∠AED＝∠AEB，∠B＝∠DAE，则△ABE∽DAE，∴△ABE∽△DCA∽△DAE，∴结论②成立，故结论①②均成立．图②F图②【方法二】翻折法证明：如解图④，∵∠BAD＋∠CAE＝90°－∠DAE＝45°，AB＝AC，∴将△ABD和△AEC分别沿AD、AE翻折后，AB、AC翻折后重合在AG上，∴BD＝DG，CE＝GE，∵∠B＝∠C＝45°，∴∠AGD＝∠AGE＝45°，∴∠DGE＝90°，G∴DG2＋GE2＝DE2，∴DE2＝BD2＋CE2.∴结论①成立；∵∠B＝∠C＝∠DAE＝45°，∠AEB＝∠C＋∠CAE＝45°＋∠CAE，∵∠CAD＝∠DAE＋∠CAE＝45°＋∠CAE，∴∠AEB＝∠CAD，则△ABE∽△DCA，图②G∵∠AED＝∠AEB，∠B＝∠DAE，则△ABE∽△DAE，∴△ABE∽△DCA∽△DAE，∴结论②成立，故结论①②均成立．图②G满分技法翻折法的思路：将等腰直角三角形的两腰分别沿45°角的两边折叠，使两直角边重合，两底角构成直角．活动3——含120°角的菱形中含半角【分析图形】如图③，已知四边形ABCD是菱形，∠BAD＝120°，点E、F分别是BC、CD上的点，∠EAF＝60°，连接AE、AF、EF.图③图③【提出问题】请根据活动1和活动2中的探究过程及结论，试判断活动3中能得到哪些结论，并写出证明过程．【解决问题】结论：△AEF是等边三角形；证明如下：如解图⑤，连接AC，四边形ABCD是菱形，∴AB＝BC＝CD＝AD，∵∠BAD＝120°，∴△ABC和△ADC都是等边三角形，∵∠EAF＝60°，∠BAD＝120°，∴∠EAC＋∠CAF＝60°，∵∠BAE＋∠EAC＝60°，∴∠CAF＝∠BAE，在△BAE和△CAF中，∴△BAE≌△CAF(ASA)，∴AE＝AF，,BAECAFBACABACF图③,BAECAFBACABACF【真题再现】1.问题背景如图，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，点E，F分别是BC，DC上的点，且∠EAF＝60°，连接AE、AF、EF，探究线段BE，EF，DF之间的数量关系．第1题图探究发现(1)如图①，小明同学的方法是将△ABE绕点A逆时针旋转120°至△ADG的位置，使得AB与AD重合，然后再证明△AFE≌△AFG，从而得出结论：_____________；EF＝BE＋DF【思维教练】证明△AFE≌△AFG，可得EF＝FG，即可得出结论；EF＝BE＋DF；图①拓展延伸(2)如图②，在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，点E，F分别是边BC，CD上的点，且∠EAF＝∠BAD，连接EF，(1)中的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；12图②12【思维教练】要探究BE，EF，DF之间三数量关系，方法同(1)即可得出结论；(1)中的结论EF＝BE＋DF仍然成立．(2)证明：如解图，将△ABE绕点A逆时针旋转至△ADG的位置，使AB与AD重合．G则∠ADG＝∠B，DG＝BE，AG＝AE，∠BAE＝∠DAG，∵∠B＋∠ADC＝180°，∴∠ADG＋∠ADC＝180°，图②∴C，D，G三点共线．∵∠FAD＋∠DAG＝∠FAD＋∠BAE＝∠BAD－∠EAF＝∠BAD，∴∠FAG＝∠EAF，又∵AF＝AF，∴△AEF≌△AGF，∴EF＝GF，又∵FG＝DG＋DF，∴EF＝BE＋DF；12G图②12归纳应用(3)如图③，在正方形ABCD中，点E，F分别是边BC，CD上的点，且∠EAF＝45°，连接EF，已知BE＝3，DF＝2，求正方形ABCD的边长．图③(3)由(1)(2)可知EF＝BE＋DF＝3＋2＝5.设正方形ABCD的边长为x，则CE＝x－3，CF＝x－2，在Rt△CEF中，EF2＝CE2＋CF2，∴25＝(x－3)2＋(x－2)2，解得x1＝6，x2＝－1(不合题意，舍去)，【思维教练】根据(1)(2)的结论和勾股定理，即可求出正方形ABCD的边长．图③