第31课时-弧长及扇形的面积-圆锥的侧面积和全面积

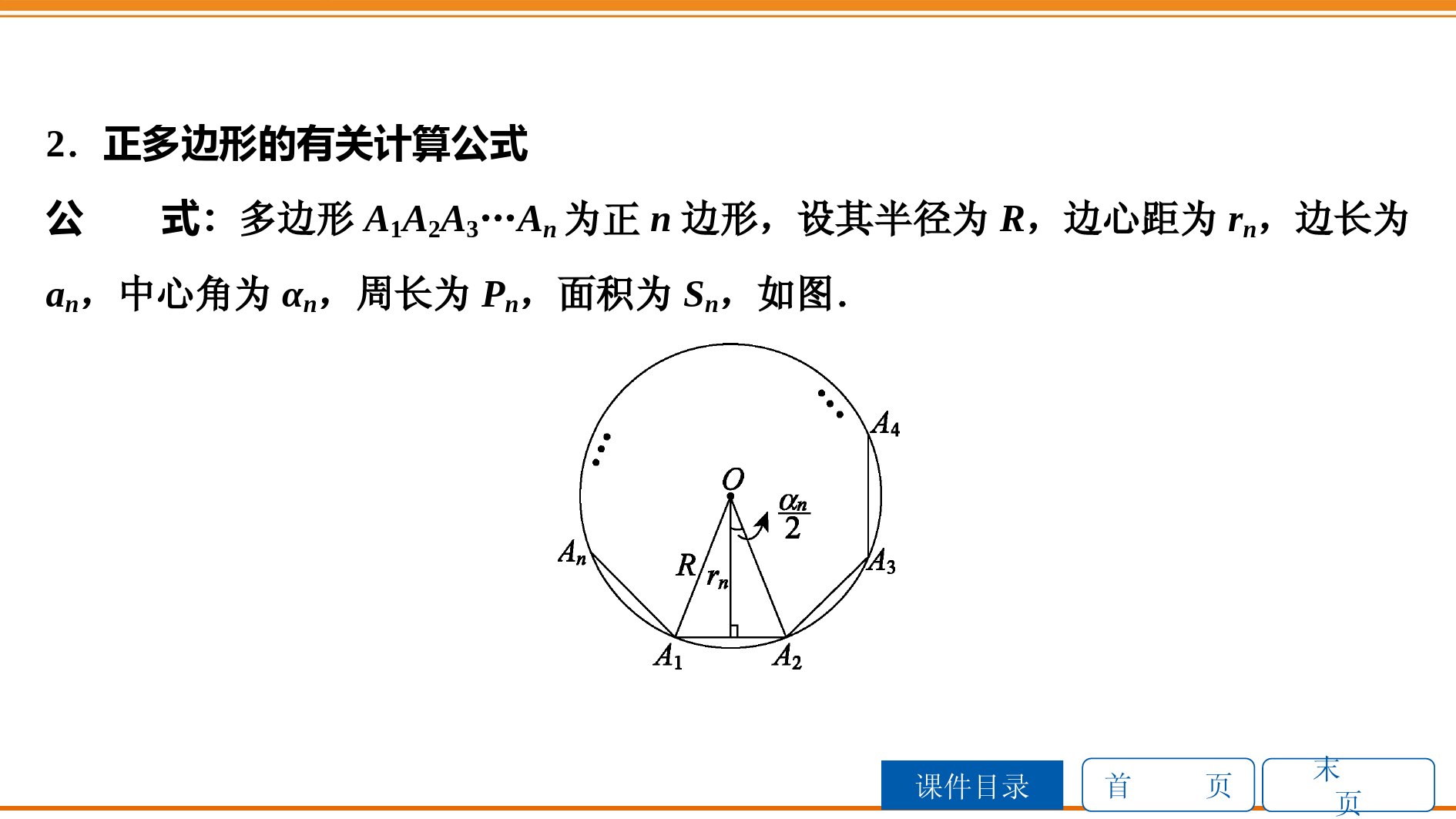
首页课件目录末页第二部分图形与几何第九章圆考点管理中考再现课时作业归类探究第31课时弧长及扇形的面积，圆锥的侧面积和全面积首页课件目录末页考点管理1．正多边形与圆的关系关系：把圆分成n(n≥3)等份，依次连接各等分点所得的多边形是这个圆的内接正n边形，这个圆就是这个正n边形的外接圆．首页课件目录末页有关概念：(1)正多边形的中心：正多边形的叫做这个正多边形的中心；(2)正多边形的半径：正多边形的叫做这个正多边形的半径；(3)正多边形的中心角：正多边形每一边所对的叫做正多边形的中心角；(4)正多边形的边心距：中心到正多边形的一边的叫做正多边形的边心距，也是正多边形内切圆的半径．外接圆的圆心外接圆的半径圆心角距离首页课件目录末页2．正多边形的有关计算公式公式：多边形A1A2A3…An为正n边形，设其半径为R，边心距为rn，边长为an，中心角为αn，周长为Pn，面积为Sn，如图．首页课件目录末页(1)中心角：αn＝360°n；(2)边长：an＝2Rsin180°n；(3)边心距：rn＝Rcos180°n；(4)周长：Pn＝nan＝2nRsin180°n；(5)面积：Sn＝n·12anrn＝12Pnrn.首页课件目录末页依据：(1)正n边形的n条半径把正多边形分成n个全等的等腰三角形．(2)正n边形的n条半径和n条边心距把正多边形分成2n个全等的直角三角形．每个直角三角形的斜边为半径，一条直角边为边心距，另一条直角边为边长的一半，其中一个锐角为中心角的一半αn2＝180°n.注意：直角三角形集中地反映了正多边形各元素之间的关系，熟悉这些关系，并且掌握直角三角形的解法，是进行正多边形有关计算的关键．首页课件目录末页3．圆的周长与弧长公式周长公式：在半径为R的圆中，圆的周长的计算公式为C＝.弧长公式：在半径为R的圆中，n°的圆心角所对的弧长的计算公式为.注意：在应用公式时，“n”和“180”不带单位．2πRl＝nπR180首页课件目录末页4．扇形定义：由组成圆心角的两条和圆心角所对的围成的图形叫做扇形．扇形的面积公式：(1)S扇形＝nπR2360；(2)S扇形＝12lR.其中，R为半径，l为扇形的弧长，n为扇形圆心角的度数．半径弧首页课件目录末页5．弓形的面积类型：如图所示．首页课件目录末页(1)当弓形所含的弧是劣弧时，如图①所示，S弓形＝S扇形OAB－S△OAB；(2)当弓形所含的弧是优弧时，如图②所示，S弓形＝S扇形OAB＋S△OAB；(3)当弓形所含的弧是半圆时，如图③所示，S弓形＝12S⊙O.方法：不规则图形的面积可以转化为规则图形(有公式可利用的图形)的面积的和或差，转化的方法一般有分割和补全两种．首页课件目录末页6．圆柱的侧面展开图展开图：圆柱的侧面展开图是一个，这个的一边长等于圆柱的高，另一边的长等于底面圆的周长．公式：如图，圆柱的高为h，底面圆的半径为R.(1)S圆柱侧＝2πRh；(2)S圆柱全＝2πRh＋2πR2.矩形矩形首页课件目录末页7．圆锥的侧面展开图展开图：沿着圆锥的一条母线把圆锥的侧面展开，得到一个，它的弧长等于圆锥底面圆的周长，它的半径等于圆锥的长．公式：如图，圆锥的母线长为l，底面圆的半径为R.(1)S圆锥侧＝12l·2πR＝πRl；(2)S圆锥全＝πRl＋πR2＝πR(l＋R)．注意：不要把圆锥的母线长误当成圆锥的高．扇形母线首页课件目录末页中考再现1．[2019·长沙]一个扇形的半径为6，圆心角为120°，则该扇形的面积是()A．2πB.4πC．12πD.24π【解析】根据扇形的面积公式，S＝120×π×62360＝12π.故选C.C首页课件目录末页2．[2019·衡阳]如图，已知圆的半径是6，则圆内接正三角形的边长是.63首页课件目录末页【解析】如答图，过点O作OD⊥BC于点D，连接OB.∵OB＝6，∠OBD＝30°，∴BD＝12BC＝33，∴BC＝63.首页课件目录末页3．[2017·岳阳]我国魏晋时期的数学家刘徽创立了“割圆术”，认为圆内接正多边形的边数无限增加时，其周长就越接近圆的周长，由此求得了圆周率π的近似值．设半径为r的圆内接正n边形的周长为L，圆的直径为d.如图所示，当n＝6时，π≈Ld＝6r2r＝3，那么，当n＝12时，π≈Ld≈.(结果精确到0.01，参考数据：sin15°＝cos75°≈0.259)3．11首页课件目录末页【解析】如答图，∠AOB＝30°，∠AOC＝15°.在Rt△AOC中，sin15°＝ACAO＝ACr≈0.259，∴AC≈0.259r.∴AB＝2AC≈0.518r.∴L＝12AB≈6.216r.∴π≈Ld≈6.216r2r＝3.108≈3.11.首页课件目录末页4．[2018·岳阳]如图，以AB为直径的⊙O与CE相切于点C，CE交AB的延长线于点E，直径AB＝18，∠A＝30°，弦CD⊥AB，垂足为点F，连接AC，OC，则下列结论中正确的是(填写序号)．①BC︵＝BD︵；②扇形OBC的面积为274π；③△OCF∽△OEC；④若点P为线段OA上一动点，则AP·OP有最大值20.25.①③④首页课件目录末页【解析】∵AB是⊙O的直径，且CD⊥AB，∴BC︵＝BD︵，故①正确．∵∠A＝30°，∴∠COB＝60°.∴S扇形OBC＝60360·π·AB22＝272π.故②错误．首页课件目录末页∵CE是⊙O的切线，∴∠OCE＝90°.∴∠OCF＝∠OEC，∠COF＝∠EOC.∴△OCF∽△OEC.故③正确．设AP＝x，则OP＝9－x.首页课件目录末页∴AP·OP＝x(9－x)＝－x2＋9x＝－x－922＋814.∴当x＝92时，AP·OP的最大值为814＝20.25.故④正确．首页课件目录末页5．[2019·张家界]如图，AB为⊙O的直径，且AB＝43，点C是AB︵上的一动点(不与点A，B重合)，过点B作⊙O的切线交AC的延长线于点D，点E是BD的中点，连接EC.(1)求证：EC是⊙O的切线；(2)当∠D＝30°时，求图中阴影部分面积．首页课件目录末页(1)证明：如答图，连接OC，BC，OE.∵AB是⊙O的直径，∴∠ACB＝∠DCB＝90°.∵点E是BD的中点，∴BE＝CE.∵OB＝OC，OE＝OE，∴△OBE≌△OCE.∵BD是⊙O的切线，∴∠OBE＝∠OCE＝90°，∴EC是⊙O的切线．首页课件目录末页(2)解：∵∠D＝30°，∠OBD＝90°，∴∠A＝60°，∴∠BOC＝120°.∵AB＝43，∴OB＝23，BE＝6，∴S阴影＝2×12×6×23－120×π×232360＝123－4π.首页课件目录末页归类探究类型之一正多边形的性质[2019·衢州]如图，取两根等宽的纸带折叠穿插，拉紧，可得边长为2cm的正六边形，则原来的纸带宽为()CA．1cmB.2cmC．3cmD.2cm首页课件目录末页【解析】如答图，过点A作AM⊥FC于点M.例3答图由正六边形的性质，得∠AFC＝60°.∵sin∠AFM＝AMAF，∴AM＝sin∠AFM·AF＝32×2＝3(cm)，AM的长即为纸带宽．故选C.首页课件目录末页1．[2018·德阳]已知圆内接正三角形的面积为3，则该圆的内接正六边形的边心距是()A．2B.1C．3D.32B首页课件目录末页【解析】如答图①，设△ABC的边长为a，由正三角形的面积公式，得S△ABC＝34a2.∴34a2＝3.解得a＝2或－2(舍去)．∴BC＝2.变式跟进1答图①变式跟进1答图②首页课件目录末页∵∠BAC＝60°，BO＝CO，∴∠BOC＝120°.∴∠OBC＝30°.∵OH⊥BC，∴BH＝12BC＝1.首页课件目录末页在Rt△BOH中，BO＝BHcos30°＝233.∴圆的半径r＝233.首页课件目录末页如答图②，正六边形内接于⊙O，且⊙O的半径为233，可知∠EOF＝60°.在△EOF中，OE＝OF，OD⊥EF，∴∠EOD＝30°.在Rt△DOE中，OD＝OE·cos30°＝233×32＝1.∴边心距为1.故选B.首页课件目录末页2．[2019·自贡]如图，图中有两张型号完全一样的折叠式饭桌，将正方形桌面边上的四个弓形面板翻折起来后，就能形成一个圆形桌面(可近似看作正方形的外接圆)，正方形桌面与翻折成的圆形桌面的面积之比最接近()A.45B.34C．23D.12C首页课件目录末页【解析】由题意可知，⊙O是正方形ABCD的外接圆，如答图，过点O点作OE⊥BC于点E，连接OC.在Rt△OEC中，∠COE＝45°，∴sin∠COE＝CEOC＝22，设CE＝k，则OC＝2CE＝2k.首页课件目录末页∵OE⊥BC，∴BE＝CE＝k，即BC＝2k.∴S正方形ABCD＝BC2＝4k2，⊙O的面积为πr2＝π·(2k)2＝2πk2.∴S正方形ABCDS⊙O＝4k22πk2＝2π≈23.故选C.首页课件目录末页类型之二扇形的弧长(1)一个扇形的圆心角是120°，它的半径是3cm，则扇形的弧长为cm.【解析】由弧长公式，得l＝120π×3180＝2π(cm)．2π首页课件目录末页(2)已知扇形的弧长为2π，圆心角为60°，则它的半径为.【解析】利用扇形的弧长公式l＝nπr180，得2π＝60πr180.∴r＝6.【点悟】熟练掌握弧长公式，理解弧长公式l＝nπR180中各个量所代表的意义是解此类题的关键．6首页课件目录末页3．[2019·绍兴]如图，△ABC内接于圆O，∠B＝65°，∠C＝70°，若BC＝22，则弧BC的长为()A．πB.2πC．2πD.22πA首页课件目录末页【解析】在△ABC中，∠A＝180°－∠B－∠C＝45°，如答图，连接OB，OC.则∠BOC＝2∠A＝90°，设圆的半径为r，由勾股定理，得r2＋r2＝(22)2，解得r＝2，∴弧BC的长为90π·2180＝π.故选A.首页课件目录末页类型之三扇形的面积[2018·成都]如图，在▱ABCD中，∠B＝60°，⊙C的半径为3，则图中阴影部分的面积是()A．πB.2πC．3πD.6πC首页课件目录末页【解析】∵四边形ABCD为平行四边形，∴AB∥CD，∠B＋∠C＝180°.又∵∠B＝60°，∴∠C＝120°.∴阴影部分的面积＝120π×32360＝3π.故选C.首页课件目录末页4．一个扇形的圆心角为135°，弧长为3πcm，则此扇形的面积是cm2.【解析】由弧长公式求得r＝4cm，∴S扇＝12lr＝12×3π×4＝6π(cm2)．6π首页课件目录末页类型之四弓形(不规则图形)的面积计算[2019·宿迁]如图，正六边形的边长为2，分别以正六边形的六条边为直径向外作半圆，与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是()A．63－πB.63－2πC．63＋πD.63＋2πA【解析】6个月牙形的面积之和为3π－π·22－6×12×2×3＝63－π.故选A.首页课件目录末页5．[2019·广安]如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝4，以BC为直径的半圆O交斜边AB于点D，则图中阴影部分的面积为()AA.4π3－3B.2π3－32C.π3－32D.π3－3首页课件目录末页【解析】∵在Rt△ABC中，∠ACB＝90°，∠A＝30°，∴∠B＝60°，∴∠COD＝120°.∵BC＝4，BC为半圆O的直径，∴∠CDB＝90°，∴OC＝OD＝2，∴CD＝32BC＝23，S阴影＝S扇形COD－S△COD＝120·π·22360－12×23×1＝4π3－3.故选A.首页课件目录末页6．[2019·山西]如图，在Rt△ABC中，∠ABC＝90°，AB＝23，BC＝2，以AB的中点O为圆心，OA的长为半径作半圆交AC于点D，则图中阴影部分的面积为()A.534－π2B.534＋π2C．23－πD.43－π2A首页课件目录末页【解析】如答图，过点D作DE⊥AB于点E，连接OD.∵∠ABC＝90°，AB＝23，BC＝2，∴∠A＝30°，∠DOB＝60°.∵AB＝23，∴AO＝OD＝3，∴DE＝32，∴S阴影＝S△ABC－S△AOD－S扇形BOD＝23－334－π2＝534－π2.故选A.首页课件目录末页7．[2019·南充]如图，在半径为6的⊙O中，点A，B，C都在⊙O上，四边形OABC是平行四边形，则图中阴影部分的面积为()A．6πB.33πC．23πD.2πA首页课件目录末页【解析】如答图，连接OB.∵四边形OABC是平行四边形，∴AB＝OC，∴AB＝OA＝OB，∴△AOB是等边三角形，∴∠AOB＝60°.∵OC∥AB，∴S△AOB＝S△ABC，∴S阴影＝S扇形AOB＝60·π×36360＝6π.故选A.首页课件目录末页8．[2019·烟台]如图，分别以边长为2的等边三角形ABC的三个顶点为圆心，以边长为半径作弧，三段弧所围成的图形是一个曲边三角形．已知⊙O是△ABC的内切圆，则阴影部分的面积为.5π3－23首页课件目录末页【解析】S△ABC＝34×22＝3，S扇形ABC＝60π·22360＝2π3，△ABC的内切圆半径为S△ABC12×2＋2＋2＝33，S△ABC的内切圆＝π·332＝π3，∴S阴影＝3S扇形ABC－S△ABC＋(S△ABC－S△ABC的内切圆)＝5π3－23.首页课件目录末页类型之五圆锥(柱)的侧面积和全面积[2019·湖州]已知圆锥的底面半径为5cm，母线长为13cm，则这个圆锥的侧面积是()A．60πcm2B.65πcm2C．120πcm2D.130πcm2【解析】∵r＝5，l＝13，∴S锥侧＝πrl＝π·5×13＝65π(cm2)．故选B.B首页课件目录末页9．[2017·绵阳]“赶陀螺”是一项深受人们喜爱的运动．如图是一个陀螺的立体结构图．已知底面圆的直径AB＝8cm，圆柱体部分的高BC＝6cm，圆锥体部分的高CD＝3cm，则这个陀螺的全面积是()A．68πcm2B.74πcm2C．84πcm2D.100πcm2C首页课件目录末页【解析】∵底面圆的直径为8cm，∴圆锥的底面半径为4cm.由勾股定理易得，圆锥的母线长为5cm.∴陀螺的全面积为π×4×5＋π×42＋8π×6＝84π(cm2)．故选C.首页课件目录末页10．[2019·金华]如图，物体由两个圆锥组成，其主视图中，∠A＝90°，∠ABC＝105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为()DA．2B.3C．32D.2首页课件目录末页【解析】∵∠A＝90°，∠ABC＝105°，∴∠ABD＝45°，∠CBD＝60°，∴△ABD是等腰直角三角形，△CBD是等边三角形．设AB长为R，圆锥底面周长为l，则BD长为2R.∵上面圆锥的侧面积为1，即1＝12lR，∴l＝2R.∴下面圆锥的侧面积为12l·2R＝12·2R·2R＝2.故选D.首页课件目录末页11．[2019·淮安]若圆锥的侧面积是15π，母线长是5，则该圆锥底面圆的半径是.3【解析】设该圆锥底面圆的半径是r，则12×2πr×5＝15π，解得r＝3.首页课件目录末页类型之六平面图形的滚动问题[2020·中考预测]如图，将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图中①位置，继续绕右下角的顶点按顺时针方向旋转90°至图中②位置，以此类推，这样连续旋转2019次．若AB＝4，AD＝3，则顶点A在整个旋转过程中所经过的路线总长为()A．2026πB.2034πC．3024πD.3030πD首页课件目录末页【解析】转动第1次，点A经过的路线长是90π·4180＝2π，转动第2次的路线长是90π·5180＝5π2，转动第3次的路线长是90π·3180＝3π2，转动第4次的路线长是0，转动第5次的路线长是90π·4180＝2π，首页课件目录末页以此类推，每4次是一个循环，故顶点A转动一个循环内的4次经过的路线长为2π＋5π2＋3π2＝6π.∵2019÷4＝504……3，∴这样连续旋转2019次后，顶点A在整个旋转过程中所经过的路线总长是6π·504＋6π＝3030π.故选D.首页课件目录末页12．[2019·凉山]如图，在△AOC中，OA＝3cm，OC＝1cm，将△AOC绕点O顺时针旋转90°后得到△BOD，则AC边在旋转过程中所扫过的图形的面积为()A.π2cm2B.2πcm2C.17π8cm2D.19π8cm2B首页课件目录末页【解析】AC边在旋转过程中所扫过的图形的面积＝S△OCA＋S扇形OAB－S扇形OCD－S△ODB，①由旋转，知△OCA≌△ODB，∴S△OCA＝S△ODB，∴①式＝S扇形OAB－S扇形OCD＝90π·32360－90π·12360＝2π(cm2)．故选B.首页课件目录末页13．[2019·扬州]如图，将四边形ABCD绕顶点A顺时针旋转45°至四边形AB′C′D′的位置，若AB＝16cm，则图中阴影部分的面积为cm2.32π【解析】由旋转的性质，得∠BAB′＝45°，四边形AB′C′D′≌四边形ABCD，则图中S阴影＝S四边形ABCD＋S扇形ABB′－S四边形AB′C′D′＝S扇形ABB′＝45π·162360＝32π(cm2)．首页课件目录末页14．[2018·恩施州]如图所示，在Rt△ABC中，AB＝1，∠A＝60°，∠ABC＝90°.将Rt△ABC沿直线l无滑动地滚动至Rt△DEF，则点B所经过的路径与直线l所围成的封闭图形的面积为.(结果不取近似值)19π12＋32首页课件目录末页【解析】在Rt△ABC中，AB＝1，∠A＝60°，∴BC＝3，∠BCB′＝150°，∠B′A′E＝120°，如答图所示．变式跟进14答图第一次滚动的半径为3，故扇形的面积为150π·32360＝5π4.首页课件目录末页第二次滚动的半径为1，故扇形的面积为120π·12360＝π3.∵△ABC的面积为12×1×3＝32，∴所求的面积为5π4＋π3＋32＝19π12＋32.首页课件目录末页15．[2018·宿迁]如图，将含有30°角的直角三角板ABC放入平面直角坐标系中，顶点A，B分别落在x轴、y轴的正半轴上，∠OAB＝60°，点A的坐标为(1,0)．将三角板ABC沿x轴向右进行无滑动的滚动(先绕点A按顺时针方向旋转60°，再绕点C按顺时针方向旋转90°……)．当点B第一次落在x轴上时，点B运动的路径与两坐标轴围成的图形面积是.3＋17π12首页课件目录末页【解析】∵∠OAB＝60°，OA＝1，∴AB＝2，BO＝3.∴S扇形ABB1＝60π·22360＝2π3，S扇形C1B1B2＝90π·32360＝3π4.∵△OAB与△ABC的面积之和为3，∴点B运动的路径与两坐标轴围成的图形面积是2π3＋3π4＋3＝3＋17π12.首页课件目录末页课时作业(68分)一、选择题(每题5分，共30分)1．[2019·温州]若扇形的圆心角为90°，半径为6，则该扇形的弧长为()A.3π2B.2πC．3πD.6πC【解析】扇形的圆心角为90°，它的半径为6，即n＝90°，r＝6，根据弧长公式l＝nπr180，得该扇形的弧长为3π.故选C.首页课件目录末页2．[2019·云南]一个圆锥的侧面展开图是半径为8的半圆，则该圆锥的全面积是()A．48πB.45πC．36πD.32π【解析】S侧＝12πr2＝12·π·82＝32π，底面圆半径为2π·82÷2π＝4，底面积为π·42＝16π，故圆锥的全面积为32π＋16π＝48π.故选A.A首页课件目录末页3．[2019·遂宁]如图，△ABC内接于⊙O，若∠A＝45°，⊙O的半径r＝4，则阴影部分的面积为()AA．4π－8B．2πC．4πD．8π－8首页课件目录末页【解析】由题意可知∠BOC＝2∠A＝45°×2＝90°，S阴＝S扇－S△OBC，S扇＝14S圆＝14π·42＝4π，S△OBC＝12×42＝8，∴S阴影＝4π－8.故选A.首页课件目录末页4．[2019·泰安]如图，将⊙O沿弦AB折叠，AB︵恰好经过圆心O，若⊙O的半径为3，则AB︵的长为()A.π2B.πC．2πD.3πC首页课件目录末页【解析】如答图，连接OA，OB，过点O作OD⊥AB交AB于点D，交AB︵于点E.由题可知，OD＝DE＝12OE＝12OA.在Rt△AOD中，sinA＝ODOA＝12，∴∠A＝30°，∴∠AOD＝60°，∠AOB＝120°，AB︵＝nπr180＝2π.故选C.首页课件目录末页5．[2018·十堰]如图，在扇形OAB中，∠AOB＝120°，OA＝12，C是OA的中点，CD⊥OA，交AB︵于点D，以OC为半径的CE︵交OB于点E，则图中阴影部分的面积是()A．12π＋183B.12π＋363C．6π＋183D.6π＋363A首页课件目录末页【解析】如答图，连接OD，AD.∵点C为OA的中点，∴OC＝12OA＝12OD.∵CD⊥OA，∴∠CDO＝30°，∠DOC＝60°.∴△ADO为等边三角形，OD＝OA＝12，OC＝CA＝6.首页课件目录末页∴CD＝122－62＝63.∴S扇形AOD＝60·π·122360＝24π，∴S阴影＝S扇形AOB－S扇形COE－(S扇形AOD－S△COD)＝120·π·122360－120·π·62360－24π－12×6×63＝12π＋183.故选A.首页课件目录末页6．[2019·菏泽]如图，在⊙O中，AB︵＝AC︵，∠ACB＝75°，BC＝2，则阴影部分的面积是()A．2＋2π3B.2＋3＋2π3C．4＋2π3D.2＋4π3A首页课件目录末页【解析】∵如答图，连接OB，OC，OA，AB︵＝AC︵，∴AB＝AC.∵∠ACB＝75°，∴∠ABC＝∠ACB＝75°，∴∠BAC＝30°，∴∠BOC＝60°.首页课件目录末页∵OB＝OC，∴△BOC是等边三角形，∴OA＝OB＝OC＝BC＝2.如答图，过点O作OD⊥BC于点D.首页课件目录末页∴BD＝CD.∵AB＝AC，∴A，O，D三点共线，∴OD＝32OB＝3，∴AD＝2＋3，∴S△ABC＝12BC·AD＝2＋3，S△BOC＝12BC·OD＝3，∴S阴影＝S△ABC＋S扇形BOC－S△BOC＝2＋3＋60π·22360－3＝2＋2π3.故选A.首页课件目录末页二、填空题(每题4分，共28分)7．[2019·杭州]如图是一个圆锥形冰淇淋外壳(不计厚度)，已知其母线长为12cm.底面圆半径为3cm.则这个冰淇淋外壳的侧面积等于cm2(结果精确到个位)．113【解析】这个冰淇淋外壳的侧面积为12×2π·3×12＝36π≈113(cm2)．首页课件目录末页8．[2019·滨州]若正六边形的内切圆半径为2，则其外接圆半径为.433首页课件目录末页【解析】如答图，连接OE，过点O作OM⊥EF于点M，则OE＝EF，EM＝FM，OM＝2，∠EOM＝30°.在Rt△OEM中，cos∠EOM＝OMOE，∴32＝2OE，解得OE＝433.即外接圆半径为433.首页课件目录末页9．[2019·齐齐哈尔]将圆心角为216°，半径为5cm的扇形围成一个圆锥的侧面，那么围成的这个圆锥的高为cm.4【解析】设圆锥底面圆半径为rcm，根据圆锥的底面周长是侧面展开图扇形的弧长可得2π·r＝216π·5180，∴r＝3.∴圆锥的高为4cm.首页课件目录末页10．[2018·常州]如图，△ABC是⊙O的内接三角形，∠BAC＝60°，BC︵的长是4π3，则⊙O的半径是.2首页课件目录末页【解析】如答图，连接OB，OC.∵∠BAC＝60°，∴∠BOC＝120°.设⊙O的半径为r.由BC︵的长为4π3，得120πr180＝43π.解得r＝2，即半径为2.首页课件目录末页11．[2019·甘肃]如图，在Rt△ABC中，∠C＝90°，AC＝BC＝2，点D是AB的中点，以A，B为圆心，AD，BD的长为半径画弧，分别交AC，BC于点E，F，则图中阴影部分的面积为.2－π2首页课件目录末页【解析】在Rt△ABC中，∵∠ACB＝90°，CA＝CB＝2，∴AB＝22，∠A＝∠B＝45°.∵D是AB的中点，∴AD＝DB＝2，∴S阴＝S△ABC－2·S扇形ADE＝12×2×2－2×45·π·22360＝2－π2.首页课件目录末页12．[2018·盐城]如图，图①是由若干个相同的图形(图②)组成的美丽图案的一部分．如图③，图形的相关数据为：半径OA＝2cm，∠AOB＝120°，则图②的周长为cm(结果保留π)．8π3首页课件目录末页【解析】∵半径OA＝2cm，∠AOB＝120°，∴AB︵的长＝120×π×2180＝4π3(cm)．由图①，得AO︵的长＋OB︵的长＝4π3(cm)，∴图②的周长＝4π3＋4π3＝8π3(cm)．首页课件目录末页13．[2019·泰安]如图，∠AOB＝90°，∠B＝30°，以点O为圆心，OA的长为半径作弧交AB于点A，点C，交OB于点D，若OA＝3，则阴影部分的面积为.3π4首页课件目录末页【解析】如答图，连接OC，过点C作CN⊥AO于点N，CM⊥OB于点M.∵∠AOB＝90°，∠B＝30°，∴∠A＝60°.∵OA＝OC，∴△AOC为等边三角形．∵OA＝3，∴CN＝332，CM＝ON＝32，∴S扇形AOC＝3π2，S△AOC＝934.首页课件目录末页在Rt△AOB中，OB＝3OA＝33，S△OCB＝943，∠COD＝30°，S扇形COD＝3π4，S阴影＝S扇形AOC－S△AOC＋S△OCB－S扇形COD＝3π4.首页课件目录末页三、解答题(共10分)14．(10分)[2019·衢州]如图，在等腰三角形ABC中，AB＝AC.以AC为直径作⊙O交BC于点D，过点D作DE⊥AB，垂足为点E.(1)求证：DE是⊙O的切线；(2)若DE＝3，∠C＝30°，求AD︵的长．首页课件目录末页(1)证明：如答图，连接OD.∵OC＝OD，AB＝AC，∴∠1＝∠C，∠C＝∠B.∴∠1＝∠B.∵DE⊥AB，∴∠2＋∠B＝90°.∴∠2＋∠1＝90°，∴∠ODE＝90°，∴DE为⊙O的切线．首页课件目录末页(2)解：连接AD.∵AC为⊙O的直径，∴∠ADC＝90°.∵AB＝AC，∴∠B＝∠C＝30°，BD＝CD.∴∠AOD＝60°.∵DE＝3，∴BD＝CD＝23，∴OC＝2.∴AD︵＝60180π·2＝2π3.首页课件目录末页(20分)15．(10分)[2019·衡阳]如图，点A，B，C在半径为8的⊙O上，过点B作BD∥AC，交OA延长线于点D，连接BC，且∠BCA＝∠OAC＝30°.(1)求证：BD是⊙O的切线；(2)求图中阴影部分的面积．首页课件目录末页(1)证明：如答图，连接OB交AC于点E.由∠BCA＝30°，∴∠AOB＝60°.在△AOE中，∵∠OAC＝30°，∴∠OEA＝90°，∴OB⊥AC.∵BD∥AC，∴OB⊥BD.又∵B在圆上，∴BD为⊙O的切线．首页课件目录末页(2)解：如答图，连接OC.由半径为8，∴OA＝OB＝8.在△AOC中，∠OAC＝∠OCA＝30°，∠COA＝120°，∴AC＝83.由∠BCA＝∠OAC＝30°，∴OA∥BC，而BD∥AC，∴四边形ACBD是平行四边形．首页课件目录末页∴BD＝83.∴S△OBD＝12×8×83＝323，S扇形OAB＝16×π×82＝32π3，∴S阴影＝323－32π3.首页课件目录末页16．(10分)[2018·达州]如图，以等边三角形ABC的边BC为直径作⊙O，分别交AB，AC于点D，E，过点D作DF⊥AC于点F.(1)求证：DF是⊙O的切线；(2)若等边三角形ABC的边长为8，求由DE︵，DF，EF围成的阴影部分的面积．首页课件目录末页(1)证明：如答图①，连接OD，CD.∵BC是⊙O的直径，∴∠BDC＝90°.∵△ABC是等边三角形，∴点D是AB的中点．∵点O是BC的中点，∴根据三角形中位线定理，得OD∥AC.∵DF⊥AC，∴OD⊥DF.∴DF是⊙O的切线．第16题答图①首页课件目录末页(2)解：如答图②，连接OE，OD，作OG⊥AC于点G，则四边形OGFD为矩形．∴FG＝OD＝12AC＝4.∵OC＝OE＝OD＝OB，且∠B＝∠C＝60°，∴△OBD和OCE均为等边三角形．∴∠BOD＝∠COE＝60°，CE＝4.∴EG＝12CE＝2，DF＝OG＝23，∠DOE＝60°.第16题答图②首页课件目录末页∴EF＝FG－EG＝OD－EG＝2.∴S阴影＝S梯形EFDO－S扇形ODE＝12×(2＋4)×23－60π×42360＝63－8π3.首页课件目录末页(12分)17．(12分)[2019·邵阳]如图，在等腰三角形ABC中，∠BAC＝120°，AD是∠BAC的平分线，且AD＝6，以点A为圆心，AD的长为半径画弧EF，交AB于点E，交AC于点F.(1)求由弧EF及线段FC，CB，BE围成图形(图中阴影部分)的面积；(2)将阴影部分剪掉，余下扇形AEF，将扇形AEF围成一个圆锥的侧面，AE与AF正好重合，圆锥侧面无重叠，求这个圆锥的高h.首页课件目录末页解：(1)∵在等腰三角形ABC中，∠BAC＝120°，∴∠B＝30°.∵AD是∠BAC的平分线，∴AD⊥BC，BD＝CD，∴BD＝3AD＝63，∴BC＝2BD＝123，∴由弧EF及线段FC，CB，BE围成图形(图中阴影部分)的面积＝S△ABC－S扇形EAF＝12×6×123－120·π·62360＝363－12π.首页课件目录末页(2)设圆锥的底面圆的半径为r，根据题意，得2πr＝120·π·6180，解得r＝2，这个圆锥的高h＝62－22＝42.