《圆锥曲线与方程》人教版高二数学选修2-1PPT课件（第2.1.1课时）.pptx

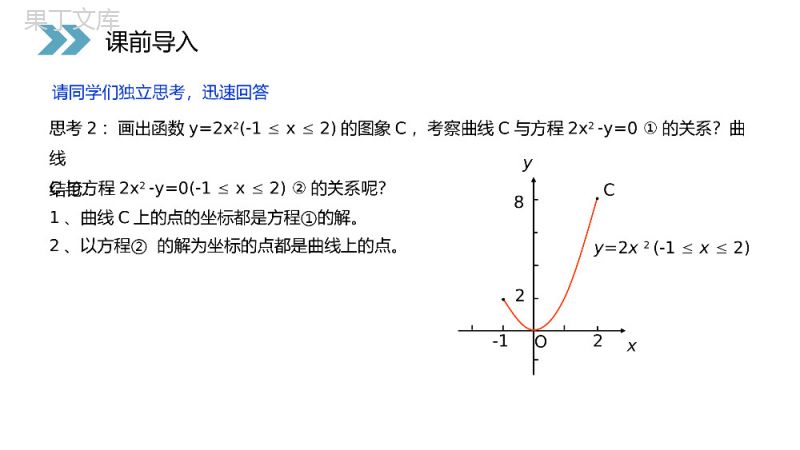
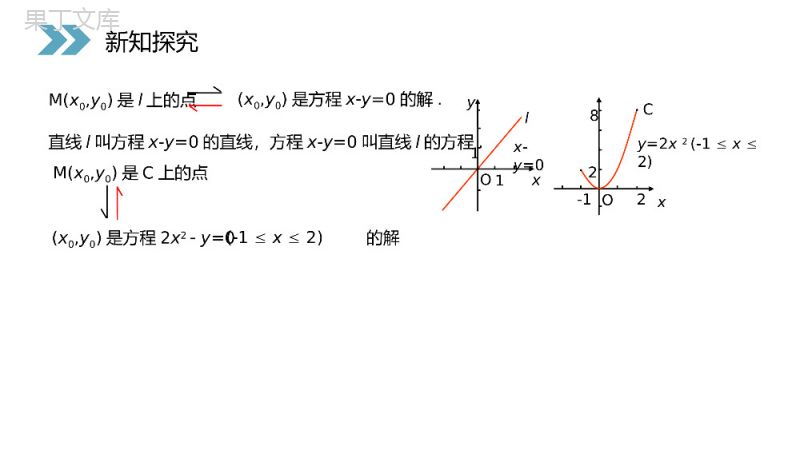
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-12.1.1圆锥曲线与方程第2章圆锥曲线与方程人教版高中数学选修2-1（1）l上点的坐标都是方程x-y=0的解（2）以方程x-y=0的解为坐标的点都在上l思考1:如图:直线l与方程x-y=0之间有什么关系？∴说直线l的方程是0xy,又说方程0xy表示的直线是l.xO11yl请同学们独立思考，迅速回答课前导入ll∴说直线l的方程是0xy,又说方程0xy表示的直线是l.思考2：画出函数y=2x2(1x2)的图象C，考察曲线C与方程2x2y=0①的关系？曲线C与方程2x2y=0(1x2)②的关系呢？yxO-128y=2x2(1x2)C2结论：1、曲线C上的点的坐标都是方程①的解。2、以方程②的解为坐标的点都是曲线上的点。请同学们独立思考，迅速回答课前导入M(x0,y0)是C上的点(x0,y0)是方程2x2y=0的解M(x0,y0)是l上的点(x0,y0)是方程xy=0的解.(1x2)直线l叫方程x-y=0的直线，方程x-y=0叫直线l的方程.x-y=0xO11yxO-128y=2x2(1x2)Cl2新知探究•定义：在直角坐标系中，如果某曲线C（看作适合某种条件的点的集合或轨迹）上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系：•①曲线上的点的坐标都是这个方程的解；•②以这个方程的解为坐标的点都是曲线上的点。•那么，这个方程叫做曲线的方程，这条曲线叫做方程的曲线。•如果曲线C的方程是f(x,y)=0，那么在曲线C上的充要条件是说明:曲线的方程——反映的是图形所满足的数量关系;方程的曲线——反映的是数量关系所表示的图形.f(x0,y0)=0p(x0,y0)新知探究练习1：请标出下列方程所对应的曲线0)1(yxyOyOxyOxxABC?这是“曲线”！请同学们迅速动手，写出答案，同桌对照,举手回答新知探究练习：请标出下列方程所对应的曲线0)1(yxyOyOxyOxxABC请同学们迅速动手，写出答案，同桌对照新知探究例1.证明与两条坐标轴的距离的积是常数k(k>0)的点的轨迹方程是xy=±k.00(1)(,)Mxy：如图，设是轨迹上的证明任意一点，oyxM00,,Mxyyx点与轴的距离为与轴的距离为0000,(,)xykxyxyk即是方程的解。请同学们独立思考，举手回答新知探究00(1)(,)Mxy：如图，设是轨迹上的证明任意一点，00,,Mxyyx点与轴的距离为与轴的距离为0000,(,)xykxyxyk即是方程的解。kyxkyxkxyyxM1111111,),()2(即即的解，是方程的坐标设点11111,,.xyMMkM而正是点到纵轴、横轴的距离，因此点到两条直线的距离的积是常数点是曲线上的点.)0()2(),1(的点的轨迹方程距离的积为常数是与两条坐标轴的可知，由kkkxyoyxM新知探究kyxkyxkxyyxM1111111,),()2(即即的解，是方程的坐标设点11111,,.xyMMkM而正是点到纵轴、横轴的距离，因此点到两条直线的距离的积是常数点是曲线上的点.)0()2(),1(的点的轨迹方程距离的积为常数是与两条坐标轴的可知，由kkkxy证明已知曲线的方程的方法和步骤：1.设M(x0,y0)是曲线C上任一点，证明(x0,y0)是方程f(x0,y0)=0的解.2.设(x0,y0)是方程f(x,y)=0的解，证明点M(x0,y0)在曲线C上.请同学们思考，必要的可以进行小组讨论，统一答案，派代表回答新知探究例2.设A，B两点的坐标分别是(-1,-1),(3,7),求线段AB的垂直平分线的方程。思考1：我们有哪些可以求直线方程的方法？0xyAB新知探究运用直线方程的知识来求.解:∵7(1)23(1)ABk,∴所求直线的斜率k=－1/2又∵线段AB的中点坐标是(1,3)，∴线段AB的垂直平分线的方程为13(1)2yx.即x+2y-7=0法一:例2.设A，B两点的坐标分别是(-1,-1),(3,7),求线段AB的垂直平分线的方程。0xyAB新知探究运用直线方程的知识来求.解:∵7(1)23(1)ABk,∴所求直线的斜率k=－1/2又∵线段AB的中点坐标是(1,3)，∴线段AB的垂直平分线的方程为13(1)2yx.即x+2y-7=0法一:y0xABM法二:若没有现成的结论怎么办──需要寻找一般性的方法例2.设A，B两点的坐标分别是(-1,-1),(3,7),求线段AB的垂直平分线的方程。新知探究法二:若没有现成的结论怎么办──需要寻找一般性的方法解:设M(x,y)是线段AB的垂直平分线上的任一点,我们的目标就是要找x与y的关系式则MA=MB需要尝试、摸索先找曲线上的点满足的几何条件∴2222(1)(1)(3)(7)xyxy坐标化∴22222121691449xxyyxxyy∴270xy化简综上所述,线段AB的垂直平分线的方程是270xy.例2.设A，B两点的坐标分别是(-1,-1),(3,7),求线段AB的垂直平分线的方程。法二:一般性的方法新知探究解:设M(x,y)是线段AB的垂直平分线上的任一点,则MA=MB需要尝试、摸索∴2222(1)(1)(3)(7)xyxy坐标化∴22222121691449xxyyxxyy∴270xy化简综上所述,线段AB的垂直平分线的方程是270xy.法二:一般性的方法⑴由上面过程可知,垂直平分线上的任一点的坐标都是方程270xy的解;证明:⑵设点1M的坐标11(,)xy是方程(Ⅰ)的解,即11270xy从而，1172xy点1M到A、B的距离分别是所以，11MAMB综上,线段AB的垂直平分线的方程是270xy.下面证明线段AB的垂直平分线的方程是x+2y-7=0.222211111211118215613;MAxyyyyy222211111211374275613;MBxyyyyy新知探究⑴由上面过程可知,垂直平分线上的任一点的坐标都是方程270xy的解;证明:⑵设点1M的坐标11(,)xy是方程(Ⅰ)的解,即11270xy从而，1172xy点1M到A、B的距离分别是所以，11MAMB综上,线段AB的垂直平分线的方程是270xy.222211111211118215613;MAxyyyyy222211111211374275613;MBxyyyyy以上过程可以概括为一句话:建设现．．．(．限．)．代化．．.新知探究第一种方法运用现成的结论当然快,但它需要你对研究的曲线要有一定的了解;第二种方法虽然有些走弯路,但这种方法有一般性.请同学们小组讨论，总结出求曲线的方程的步骤。√√√√√求曲线的方程(轨迹方程),一般有下面几个步骤:1.建立适当的坐标系,设曲线上任一点M的坐标;2.写出适合条件P的几何点集:;3.用坐标表示条件,列出方程;4.化简方程为最简形式;5.证明(查漏除杂).以上过程可以概括为一句话:建设现．．．(．限．)．代化．．.√√√√√xy0(0,2)(,)xyF..MlB请同学们独立思考，效仿例题，完成本题新知探究例3,已知一条直线和它上方的一个点F,点F到的距离是2.一条曲线也在的上方,它上面的每一点到F的距离减去到的距离的差都是2,建立适当的坐标系,求这条曲线的方程.xy0(0,2)(,)xyF..Mlxy0(0,2)(,)xyF..MlB例2已知一条直线和它上方的一个点F,点F到的距离是2.一条曲线也在的上方,它上面的每一点到F的距离减去到的距离的差都是2,建立适当的坐标系,求这条曲线的方程.新知探究xy0(0,2)(,)xyF..Ml以上过程可以概括为一句话:建设现．．．(．限．)．代化．．.√√√√√求曲线的方程(轨迹方程),一般有下面几个步骤:1.建立适当的坐标系,设曲线上任一点M的坐标;2.写出适合条件P的几何点集:;3.用坐标表示条件,列出方程;4.化简方程为最简形式;5.证明(查漏除杂).限(找几何条件)、代(把条件坐标化)建立坐标系设点的坐标化简方法小结以上过程可以概括为一句话:建设现．．．(．限．)．代化．．.√√√√√1.如果曲线（或轨迹）有对称中心，通常以对称中心为原点.3.尽可能使曲线上的关键点在坐标轴上.2.如果曲线（或轨迹）有对称轴，通常以对称轴为坐标轴.建立坐标系的要点是什么？方法小结∵点M与x轴的距离为y,22(4)FMxy∴y=22(4)xy∴222816yxyy∴2816xy一：直接法方法小结练习1.已知点M与轴的距离和点M与点F(0,4)的距离相等,求点M的轨迹方程.解:设点M的坐标为(x,y)建立坐标系设点的坐标限(找几何条件)代(把条件坐标化)化简这就是所求的轨迹方程.∵点M与x轴的距离为y,22(4)FMxy∴y=22(4)xy∴222816yxyy∴2816xy求曲线方程的一般步骤：(1)建立适当的坐标系，用有序实数对（x,y）表示曲线上任意一点M的坐标(2)写出适合条件P的点M的集合P={Mp(M)}(3)用坐标表示条件P(M),列出方程f(x,y)=0.(4)画方程f(x,y)=0为最简形式。(5)说明以化简后的方程的解为坐标的点都在曲线上。方法小结感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明1.曲线的方程、方程的曲线2.点在曲线上的充要条件3.证明已知曲线的方程的方法和步骤4.求曲线方程的一般步骤内容回顾讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-1感谢你的聆听第2章圆锥曲线与方程人教版高中数学选修2-1