第7章-面板数据模型分析,动态面板数据模型

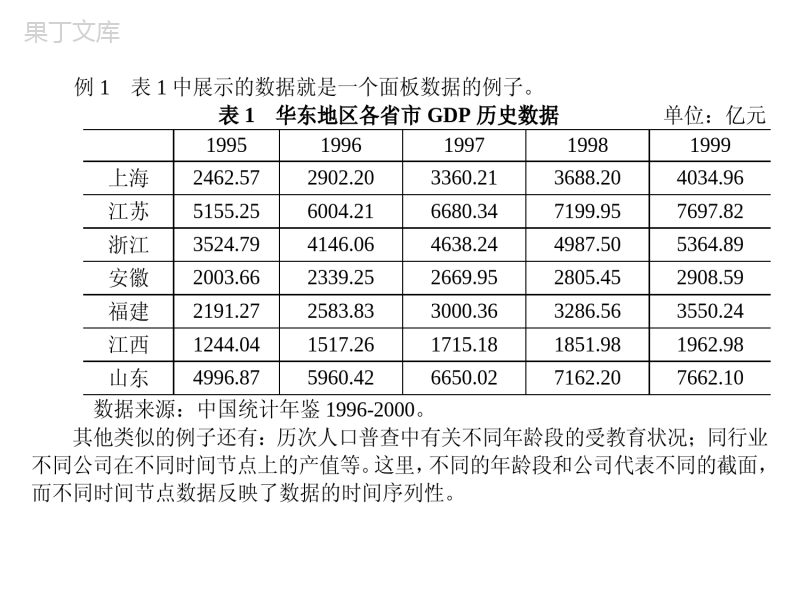
面板数据模型的分析第一节面板数据模型简介第二节固定效应模型及其估计方法第三节随机效应模型及其估计方法第四节模型设定的检验第五节面板数据模型应用实例第一节面板数据模型简介一、面板数据和模型概述时间序列数据或截面数据都是一维数据。例如时间序列数据是变量按时间得到的数据；截面数据是变量在截面空间上的数据。面板数据（paneldata）也称时间序列截面数据（timeseriesandcrosssectiondata）或混合数据（pooldata）。面板数据是同时在时间和截面空间上取得的二维数据。简单地讲，面板数据因同时含有时间序列数据和截面数据，所以其统计性质既带有时间序列的性质，又包含一定的横截面特点。因而，以往采用的计量模型和估计方法就需要有所调整。例1表1中展示的数据就是一个面板数据的例子。表1华东地区各省市GDP历史数据单位：亿元19951996199719981999上海2462.572902.203360.213688.204034.96江苏5155.256004.216680.347199.957697.82浙江3524.794146.064638.244987.505364.89安徽2003.662339.252669.952805.452908.59福建2191.272583.833000.363286.563550.24江西1244.041517.261715.181851.981962.98山东4996.875960.426650.027162.207662.10数据来源：中国统计年鉴1996-2000。其他类似的例子还有：历次人口普查中有关不同年龄段的受教育状况；同行业不同公司在不同时间节点上的产值等。这里，不同的年龄段和公司代表不同的截面，而不同时间节点数据反映了数据的时间序列性。研究和分析面板数据的模型被称为面板数据模型（paneldatamodel）。它的变量取值都带有时间序列和横截面的两重性。一般的线性模型只单独处理横截面数据或时间序列数据，而不能同时分析和对比它们。面板数据模型，相对于一般的线性回归模型，其长处在于它既考虑到了横截面数据存在的共性，又能分析模型中横截面因素的个体特殊效应。当然，我们也可以将横截面数据简单地堆积起来用回归模型来处理，但这样做就丧失了分析个体特殊效应的机会。面板数据通常分为两类：•由个体调查数据得到的面板数据通常被称为微观面板（micropanels）。•微观面板数据的特点是个体数N较大（通常是几百或几千个），而时期数T较短（最少是2年，最长不超过10年或20年）。•由一段时期内不同国家的数据得到的面板数据通常被称为宏观面板（macropanels）。•这类数据一般具有适度规模的个体N（从7到100或200不等，如七国集团，OECD，欧盟，发达国家或发展中国家），时期数T一般在20年到60年之间。•对于宏观面板，当时间序列较长时需要考虑数据的非平稳问题，如单位根、结构突变以及协整等；而微观面板不需要处理非平稳问题，特别是每个家庭或个体的时期数T较短时。面板数据的优点（１）可以控制个体异质性可以克服未观测到的异质性（unobservedheterogeneity）这种遗漏变量问题。这个异质性是指在面板数据样本期间内取值恒定的某些遗漏变量。（2）面板数据模型容易避免多重共线性问题•面板数据具有更多的信息；•面板数据具有更大的变异；•面板数据的变量间更弱的共线性；•面板数据模型具有更大的自由度以及更高的效率。（3）与纯横截面数据或时间序列数据相比，面板数据模型允许构建并检验更复杂的行为模型。二、一般面板数据模型介绍•用面板数据建立的模型通常有3种。即混合估计模型、固定效应模型和随机效应模型。•混合（pool）估计模型。•如果从时间上看，不同个体之间不存在显著性差异；从截面上看，不同截面之间也不存在显著性差异，那么就可以直接把面板数据混合在一起用普通最小二乘法（OLS）估计参数。二、一般面板数据模型介绍符号介绍：ity——因变量在横截面i和时间t上的数值；jitx——第j个解释变量在横截面i和时间t上的数值；假设：有K个解释变量，即Kj,,2,1；有N个横截面，即Ni,,2,1；时间指标Tt,,2,1。记第i个横截面的数据为iTiiiyyyy21；KiTiTiTKiiiKiiiixxxxxxxxxX212221212111；iTiii21其中对应的i是横截面i和时间t时随机误差项。再记Nyyyy21；NXXXX21；N21；K21这样，y是一个1TN的向量；X是一个KTN的矩阵；而μ是一个1TN的向量。针对这样的数据，有以下以矩阵形式表达的面板数据模型：Xy（1）方程（1）代表一个最基本的面板数据模型。基于对系数β和随机误差项μ的不同假设，从这个基本模型可以衍生出各种不同的面板数据模型。最简单的模型就是忽略数据中每个横截面个体所可能有的特殊效应，如假设),0(~2iid，而简单地将模型视为横截面数据堆积的模型。但是由于面板数据中含有横截面数据，有时需要考虑个体可能存在的特殊效应及对模型估计方法的影响。例如在不同个体误差项存在不同分布的情况下，OLS估计量虽然是一致的，但不再是有效估计量，因此往往需要采用GLS。一般为了分析每个个体的特殊效应，对随机误差项it的设定是itiit（2）其中i代表个体的特殊效应，它反映了不同个体之间的差别。最常见的两种面板数据模型是建立在i的不同假设基础之上。一种假设假定i是固定的常数，这种模型被称为固定效应模型（fixedeffectmodel），另一种假设假定i不是固定的，而是随机的，这种模型被称为随机效应模型（randomeffectmodel）。几点说明•未观测到的异质性可能不会随着样本的变化而变化，也可能随着样本的变化而发生随机的变化。•不同截距的数据生成过程就是这未观测到的差别不随样本而变化的数据生成过程。•误差成份（errorcomponents）数据生成过程就是这未观测到的差别随样本而随机变化的数据生成过程。•在不同截距的数据生成过程中，各自不同的截距都是参数。误差成份模型有两种情况，一是随机的个体效应与解释变量无关，一种是随机的个体效应与解释变量相关。•所谓双因素效应模型，就是在模型中既考虑了不可观测非时变的（个体）异质效应，又考虑了不可观测时变（个体）同质效应的模型。•类似地，双因素效应模型也有固定效应和随机效应之分，如果设定个体效应αi和时间效应λt是确定的，就是双因素固定效应模型；如果设定个体效应αi和时间效应λt是随机的，就是双因素随机效应模型。在实际应用时，模型的正确设定必须进行相关的统计检验。第二节固定效应模型及其估计方法一、固定效应模型的形式在固定效应模型中假定itiit其中i是对每一个个体是固定的常数，代表个体的特殊效应，也反映了个体间的差异。ititiitxy整个固定效应模型可以用矩阵形式表示为：NNNNxxxiiiyyy21212121000000其中i为1T的单位向量。进一步定义：iiidddDN00000021id为1TN向量，是一个虚拟变量（dummyvariable）。模型可以再写为：xDy其中D是一个有虚拟变量组成的矩阵。因此固定效应模型也被称为最小二乘虚拟变量模型（leastsquaresdummyvariable(LSDV)model），或简单称为虚拟变量模型。二、固定效应模型的估计和检验固定效应模型中有N个虚拟变量系数和K个解释变量系数需要估计，因此总共有N+K个参数需要估计。当N不是很大时，可直接采用普通最小二乘法进行估计。但是当N很大时，直接使用OLS方法的计算量就变得非常大，甚至有可能超过计算机的存储容量。一个解决问题的办法就是分成两步来对面板数据模型进行回归分析。由这种方法导出的估计量常被称为组内估计量（withingroupestimator），有时也记为wˆ。第一步，剔除虚拟变量在模型中的影响，然后再对参数β进行估计。剔除虚拟变量D影响的办法就是利用下列矩阵对所有变量进行“过滤”。设DDDDPD1)(，其中D的定义与方程前所述。设DDPIM，用DM转变模型xDy。显然0DMD，则有DDDMXMyM用OLS得到β的估计：yMXXMXDDw1)(ˆ组内估计量与对下列方程的OLS估计量是等同的。)(iitiitXXyy+随机误差项其中，iy和iX代表各自变量个体的均值。上式中，OLS估计量主要利用的是个体变量对其均值偏离的信息，随机误差项也仅反映对其个体均值的偏离波动，这是该估计量被称为组内估计量的原因。第二步，估计参数α。由于已经得到了β的估计值，所以α的估计就变得比较简单。)ˆ()(ˆ1wXYDDDˆ其实就是用自变量和解释变量的个体均值和wˆ按下列模型计算出的误差项：wiiiXyˆˆ估计量wˆ和ˆ的方差估计：122ˆ)(ˆXPXsDwiiXXTswiˆ22ˆˆˆ其中2s是对误差项方差的估计量：KNNTxysitwitiit22)ˆˆ(注意：在对误差项方差的估计量中，分母（NT-N-K）反映了整个模型的自由度。有了这些方差的估计量，就可以用传统的t-统计量对估计系数的显著性进行检验。同时，还可以运用下列F-统计量对jiji,的原假设进行检验：)/()1()1/()(),1(222KNNTRNRRKNNTNFURU其中2UR代表无约束回归模型2R，而2RR为有约束回归模型的2R，约束条件即为原假设。相对于组内估计量，另外还有一种估计量称为组间估计量（betweengroupestimator）。定义为：yPXXPXDDB1)(ˆ它其实是下列模型的OLS估计量：iiixy因而可以被看作利用不同的个体均值信息所作出的估计。组间估计量一般而言是一致估计量，但不是有效的。因为它只是利用了个体均值的信息。组内估计量在这个意义上与组间估计量是相对的，因为组内估计量利用的正是被组间估计量所“抛弃”的部分信息。固定效应模型的优点：能够确定地反映个体之间的差距及其简单的估计方法；固定效应模型的缺点：存在模型自由度比较小（因为有N个截距系数）和存在对个体差异的限制性假设（即个体间差异为固定的）。第三节随机效应模型及其估计方法一、随机效应模型的形式类似固定效应模型，随机效应模型也假定：itiit但与固定效应模型不同的是，随机效应模型假定i与it同为随机变量随机效应模型可以表达如下：iiiiiXy（18）其中iy和i均为1T向量；iX是KT矩阵；i是一个随机变量，代表个体的随机效应。由于模型的误差项为二种随机误差之和，所以也称该模型为误差构成模型（errorcomponentmodel）。还假定：(1)i和itx不相关；(2)0)()(iitEE；(3)tjiEjit,,,0)(;(4)stjiEjsit或,0)(;(5)jiEji,0)((6)tiEit,),(22;(7)iEi),(22。给定这些假设，随机效应面板数据模型也可同样写为：y=Xβ+μ其中)(iIn，α的向量形式与以前相同。是Kronecker乘法符号。例2Kronecker乘法：121212200iiiI例3前面的矩阵D也可用Kronecker乘法表示：1TNiID在这些假设的情况下，简单OLS估计量仍然是无偏和一致的，但不是有效的。因为：iiIVarTi22)(（19）NNNTIiiIIVar22)(（20）同一个个体、不同时间节点上的随机误差项之间存在一定的相关性，而OLS没有利用方差矩阵中含有的这些信息，因而不再是最有效的估计量。因此有必要采用GLS。二、随机效应模型的估计1.2和2已知时——直接采用GLS定义下列符号：TTNTTTTNiiTIiiiiIP1))((1（21）PIQNT（22）在以上这些符号的意义下，可以算出Σ-1的计算公式：)(1221PQ（23）其中2222T注：（1）Σ-1的表达式说明只要知道2和2，就可以推导出Σ-1。（2）由于Q和P都是幂等矩阵（idempotentmatrix）以及Q和P间存在正交性，所以Σ-1/2可以表示为：)(2/1PQ（24）其中，/1是一个实数常数，它在GLS中相互抵消，没有任何影响，我们无须考虑它，因此Σ-1/2还可以表示为：TiiIITTTN)1(2/1（25）注意：上式说明在两种情况下，可以不使用GLS：（1）当2相对于2很小而T有限时，1，可直接采用OLS；（2）当T很大，以至0,22T，可直接采用组内估计方法。对β的估计直接采用GLS方法：yXXXGLS111)(ˆ（26）或NiiiNiiiGLSyXXX11111ˆ（27）上述两式是等同的，它们还等同于：在方程（18）两边乘以Ω-1/2，再进行OLS估计，即iiiiiXy2/12/12/1（28）另外，在前面七个假定下，GLSˆ的协方差矩阵为：11)()ˆ(XXVarGLS（29）注：GLSˆ是无偏和有效估计量。2.2和2未知时——采用可行的广义最小二乘（FGLS）方法如果没有2和2的信息，就必须要首先运用数据对它们进行估计。因为我们的目的是得到Σ的一致估计值，然后进行FGLS，所以需要对2和2的一致估计。在这种情况下，GLS估计量是一致的和渐进有效的（asymptoticallyefficient）。一致估计量要求：当样本量趋近无穷大时，估计量同时趋近真实值。在面板数据模型中这就要求N和T分别趋向无穷大，这有时有问题，如例1中，N是固定的，华东六省一市是不能改变的，因此当样本的N和T都比较小时，可以直接采用固定效应模型。估计的步骤如下：第一步，估计2和θ：利用前面提到的组内估计量和组间估计量相关的误差项22)1(ˆpwwTNSSE（30）2221ˆTNSSEpBB（31）其中SSE代表估计模型中随机误差项的平方和。由此可对2和θ进行估计（其中222ˆBwT）。第二步，求Σ-1的一致估计量（利用式（23））。第三步，按Σ已知的情况下对β进行估计：yXXXFGLS111ˆ)ˆ(ˆ（32）3.小结：GLS估计量、组内估计量和组间估计量之间的关系由三种估计量的表达式可得出如下的等式关系：BwGLSFFˆ)1(ˆˆ（33）其中：iiiXXBitiitiitXXwXXwXXBXXwxxxxTSxxxxSTSSSF))(())((22221几点说明：（1）GLS估计量恰好是组内估计量和组间估计量的加权平均；（2）当T很大，0时，可得F=1，则GLS估计量与组内估计量是一样的，和前面讨论的结果一致；（3）组内估计时忽略了组间的变化，组间估计时忽略了组内的变化，而OLS是对两者赋予了相等的权重。（4）随机效应模型的优点：能够反映个体之间差距的随机性；与固定效应模型相比，需要估计的模型系数也比较少，因而模型的自由度比较高；（5）缺点：面板数据模型中含有横截面数据，在模型的误差项中很可能出现异方差，与基本假设产生矛盾；随机效应模型有可能因没有包括某些必要的解释变量而导致模型设定出现错误。（为什么？）第四节模型设定的检验一、协方差分析检验二、固定效应和随机效应的检验三、面板单位根和协整检验模型(1)常用的有如下三种情形：情形情形11：：((不变系数模型不变系数模型))情形情形22：：((变截距模型变截距模型))情形情形33：：((变参数模型变参数模型))对于情形1，在横截面上无个体影响、无结构变化，则普通最小二乘法估计给出了和的一致有效估计。相当于将多个时期的截面数据放在一起作为样本数据。对于情形2，称为变截距模型，在横截面上个体影响不同，个体影响表现为模型中被忽略的反映个体差异的变量的影响，又分为固定影响和随机影响两种情况。jijiββ,jijiββ,jijiββ,一一协方差分析检验（可混合性检验）协方差分析检验（可混合性检验）经常使用的检验是协方差分析检验，主要检验如下两个假设：H1：H2：可见如果接受假设H2则可以认为样本数据符合情形1，即模型为不变参数模型不变参数模型，无需进行进一步的检验。如果拒绝假设H2，则需检验假设H1。如果接受Nβββ21N21Nβββ21下面介绍假设检验的F统计量的计算方法。首先计算情形3(变参数模型变参数模型)的残差平方和，记为S1；情形2(变截变截距模型距模型)的残差平方和记为S2；情形1(不变参数模型不变参数模型)的残差平方和记为S3。计算F2统计量(10.2.7)在假设H2下检验统计量F2服从相应自由度下的F分布。若计算所得到的统计量F2的值不小于给定置信度下的相应临界值，则拒绝假设H2，继续检验假设H1。反之，接受H2则认为样本数据符合模型情形1，即不变参不变参)]1(),1)(1[(~))1(()]1)(1/[()(1132kTNkNFkNNTSkNSSF在假设H1下检验统计量F1也服从相应自由度下的F分布，即(10.2.8)若计算所得到的统计量F1的值不小于给定置信度下的相应临界值，则拒绝假设H1。如果接受H1，则认为样本数据符合情形2，即模型为变截距模型变截距模型，反之拒绝H1，则认为样本数据符合情形3，即模型为变参数模型变参数模型。)]1(,)1[(~))1((])1/[()(1121kTNkNFkNNTSkNSSF二二HausmanHausman检验检验Hausman（1978）等学者认为应该总是把个体影响处理为随机的，即随机影响模型优于固定影响模型，其主要原因为：固定影响模型将个体影响设定为跨截面变化的常数使得分析过于简单，并且从实践的角度看，在估计固定影响模型时将损失较多的自由度，特别是对“宽而短”的面板数据。但相对于固定影响模型，随机影响模型也存在明显的不足：在随机影响模型中是假设随机变化的个体影响与模型中的解释变量不相关，而在实际建模过程中这一假设很有可能由于模型中省略了一些变量而不满足，从而导致估计结果出现不一致性。HausmantestHausman检验的前提是如果模型包含随机效应，它应与解释变量相关。因此在原假设H0：随机效应与解释变量不相关的假定下，组内估计量（对虚拟变量模型）和GLS得出的估计量均是一致的，但是组内估计量不是有效的；在备择假设H1：随机效应与解释变量相关的假定下，GLS不再是一致的，而组内估计量仍是一致的。因此在原假设下，wˆ与GLSˆ之间的绝对值差距应该不大，而且应该随样本的增加而缩小，并渐进趋近于0。而在备择假设下，这一点不成立。Hausman利用这个统计特点建立了以下检验统计量：)ˆˆ()ˆˆ(1GLSwGLSwW（35）注意：这里的与前面提到的Σ有所不同，这里表示β的两种估计量协方差矩阵之差（Hausman的一个基本结论就是有效估计量和其与非有效估计量之差（即：)ˆˆ(GLSw）的协方差等于0，所以GLSwGLSwˆvarˆvar)ˆˆvar(），即：GLSwˆvarˆvar（36）Hausman统计量即Wald统计量渐进服从自由度为K的2分布：)(2KWd（37）几点说明•原假设成立时，则随机效应比固定效应更有效。•如果正确的模型是第一个或第二个误差成份数据生成过程，那么Hausman检验能很好地将二者区别开来。•但存在一种可能，解释变量中存在测量误差，这时固定效应和随机效应估计量都是不一致的，但二者导致的偏误有所不同。通常固定效应估计量的测量误差偏误会更大。这时要谨慎对待检验结果。•此时工具变量估计量是更好的选择。在不存在一个好的工具变量情况下，使用随机效应估计量好于固定效应估计量。小结•面板数据是我们有机会避免一种特殊的遗漏变量偏误，如果对同一个个体，被遗漏变量在不同时期保持不变，面板数据集的时间维度就可以控制这种未观测到的异质性。•个体误差成份与解释变量不相关的误差成份DGP的有效估计量，就是成为随机效应估计量的一个可行GLS估计量。它在对观测赋予权重时很好地解释了个人干扰之间的相关性。如果个体误差成份与解释变量相关，那么随机效应就不是一致估计量，此时固定效应再次成为有效的估计量。•到底是设定一个不同截距的DGP还是设定一个误差成份的DGP，主要取决于抽样背景。建立一个研究10家企业投资需求状况的PanelData模型：t=1,2,…,20其中：企业标识数字从1~10，分别对应通用汽车（GM）、克莱斯勒（CH）、通用电气（GE）、西屋（WE）和美国钢铁（US）等。被解释变量It分别是10家企业的总投资。解释变量为Mt分别是10家企业前一年企业市场价值（反映企业的预期利润）；Kt分别是10家企业前一年末工厂存货及设备价值（反映企业必要重置投资期望值）。应用实例应用实例tttituβKβMαI21Stata例子•webusegrunfeldxtsetcompanyyearxtdesxtlineinvest混合回归：reginvestmvaluekstock固定效应：xtreginvestmvaluekstock,fe随机效应：xtreginvestmvaluekstock,rextreginvestmvaluekstock,feeststorefixedxtreginvestmvaluekstock,reeststorerandomhausmanfixedrandom本题接受原假设，即应该用随机效应。双向固定效应模型•固定效应模型：Yit=ai+XitB+εit•双向固定效应模型：Yit=ai+ft+XitB+εit•实际上添加了t-1个时间虚拟变量。主要反应随着时间变化的一些特征。tabyear,gen(yr)editdropyr1xtreginvestmvaluekstockyr,fe大部分时间虚拟变量显著，说明随着时间的变动，invest有不断变动的趋势。