湘教版数学九年级上册-《比例线段(1)》参考课件4

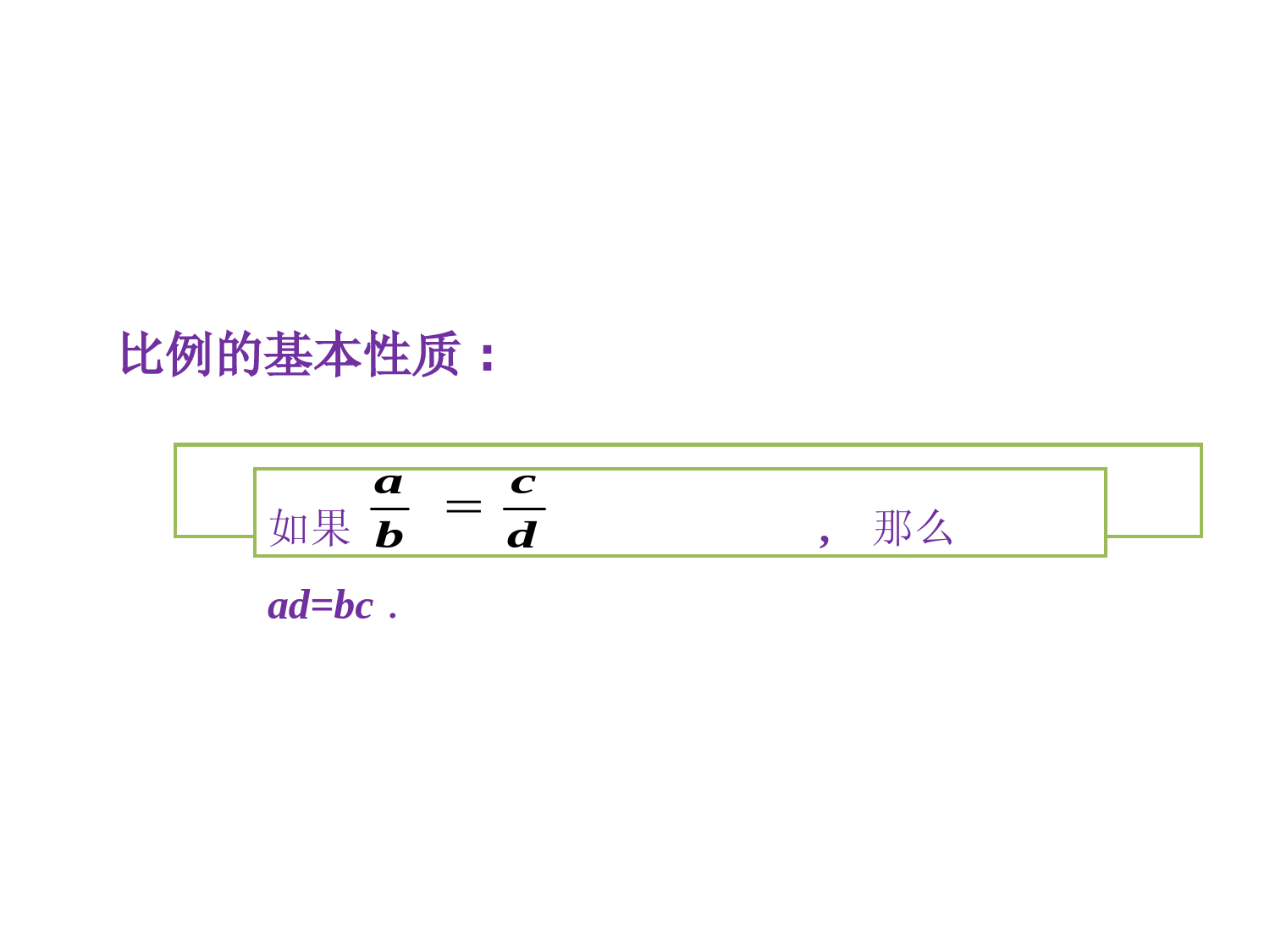
第3章图形的相似3.1比例线段3.1比例线段—比例的基本性质复习回顾在小学，我们已经知道，如果两个数的比值与另外两个数的比值相等，就说这四个数成比例.现在我们学习了实数，把这四个数理解为实数，写成式子就是：acbd如果a:b=c:d或，则称a，b，c，d成比例，其中b，c称为比例内项，a，d称为比例外项.如果a，b，c，d成比例，即，那么ad=bc吗？dcba在式子两边同乘bd，得ad=bc.acbd比例的基本性质:如果,那么ad=bc．dcba如果ad=bc，其中a,b,c,d为非零实数，那么成立吗？与同伴交流！acbd例1已知四个非零实数a，b，c，d成比例，下列各式成立吗？若成立，请说明理由.acbd①①,bdac②②.abcdbd④④,abcd③③由此得到.abcdbd由于两个非零数相等，则它们的倒数也相等，因此，由①式可以立即得到②式，即②式成立.由①式得ad=bc..abcd在上式两边同除以cd，得11.acbd在①式两边都加上1，得3.1比例线段—比例的基本性质重点、难点重点：线段的比和成比例线段的概念及其有关计算.黄金分割的定义及黄金分割比的探索.难点：判断四个数或四条线段成比例.黄金分割点的定义及相关计算类问题.如图3-1，在方格纸上（设小方格边长为单位1）有△ABC和△A′B′C′，它们的顶点都在格点上.试求出线段AB，BC，AC，A′B′，B′C′，A′C′的长度，并计算AB与A′B′，BC与B′C′，AC与A′C′的长度的比值.一般地，如果选用同一长度单位量得两条线段AB，A′B′的长度分别为m，n，那么把它们的长度的比叫作这两条线段AB与A′B′的比(ratio)，记作，或AB∶A′B′＝m∶n.如果的比值为k，那么上述式子也可写成：或AB＝ｋ·A′B′.mn''ABmnAB''ABkABmn在四条线段中，如果其中两条线段的比等于另外两条线段的比，那么这四条线段叫作成比例成比例线段线段，简称为比例线段比例线段.例如，已知四条线段a，b,c，d，若，则a，b，c，d是比例线段.acbd已知线段a，b，c，d的长度分别为0.8cm，2cm，1.2cm，3cm，问a，b，c，d是比例线段吗？例题探究∴，即a，b，c，d是比例线段.acbd0.81.2=0.40.4,23acbd，解：黄金分割黄金分割古希腊数学家、天文学家欧多克塞斯(Eudoxus，约前400—约前347)曾经提出一个问题：能否将一条线段AB分成不相等的两部分，使较短线段CB与较长线段AC的比等于线段AC与原线段AB的比？即使得成立？CBACACAB如果这能做到的话，那么称线段AB被点C黄金分割，点C叫作线段AB的黄金分割点，较长线段AC与原线段AB的比叫作黄金分割比.如图，设线段AB的长度为1个单位，AC的长度为x个单位，则CB的长度为(1-x)个单位.CBACACAB①根据①式，列出方程：②11xxx由于x≠0，因此方程②两边同乘x，得1–x=x2，即x2+x-1=0.③510.618,2ACAB因为解得（舍去）.215,21521xx所以我们一定可以把一条线段黄金分割，黄金分割比为,它约等于0.618.215线段黄金分割的比值引起了人们极大的注意.许多建筑物的轮廓矩形(例如古希腊时期的巴台农神庙的正面轮廓矩形)的高与宽之比，门窗的宽与高之比都约等于0.618，这样看上去美观.巴台农神庙印度泰姬陵正面高度与底部宽度之比约为黄金分割比.著名画家达•芬奇的蒙娜丽莎构图就完美的体现了黄金分割在油画艺术上的应用.通过上面两幅图片可以看出来，蒙娜丽莎的头和两肩在整幅画面中都处于完美的体现了黄金分割，使得这幅油画看起来是那么的和谐和完美.线段之间的一种数量关系：四条线段成比例.感受到成比例线段围成的图形在形状上也有美妙的关系！认识了一个最特别的数，比值是它的线段围成的图形最美丽.510.6182