分式的基本性质第1课时(基本性质)-八年级数学上册同步教材配套精品教学课件(人教版)

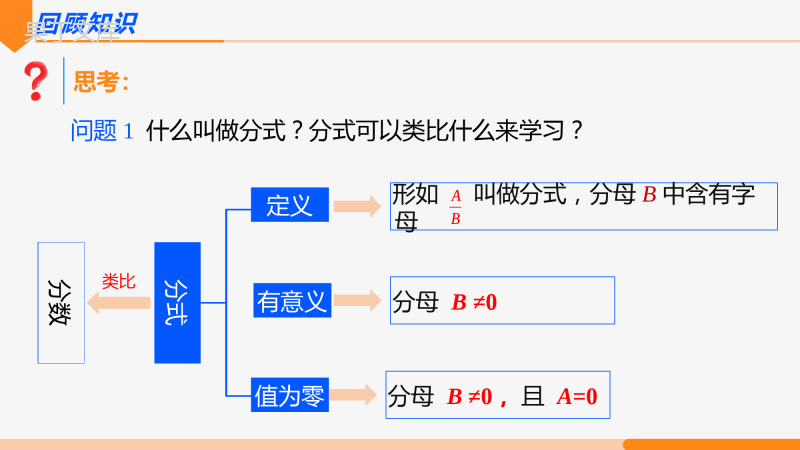
第十五章分式分式的基本性质15.1分式第1课时回顾知识思考：问题1什么叫做分式？分式可以类比什么来学习？分数定义类比分式值为零有意义形如叫做分式，分母B中含有字母AB分母B≠0分母B≠0，且A=0AB新知探究思考：问题2根据分数的基本性质，类比得出分式的基本性质？22=,33cc44.55cc22=,33cc44.55cc归纳知识分式的基本性质0AACAACCBBCBBC（）,.其中A,B,C是整式.分式的分子与分母乘（或除以）同一个不等于0的整式，分式的值不变0AACAACCBBCBBC（）,.针对练习1.下列式子从左到右的变形一定正确的是()A.B.C.D.+33aabbaacbbc33aabb22aabb2.如果把中的x与y都扩大到原来的20倍，那么这个式子的值()A．不变B．扩大到原来的10倍C．扩大到原来的20倍D．缩小到原来的5xxy120CA+33aabbaacbbc33aabb22aabb5xxy120典例讲解例1填空：（1）3,xxyy（）22336xxyxyx；（）332.xxxxxyxyxy222233333=.6632（）（）（）xxyxxyxxyxxxx3,xxyy（）22336xxyxyx；（）332.xxxxxyxyxy222233333=.6632（）（）（）xxyxxyxxyxxxx典例讲解例1填空：（1）（2）3,xxyy（）2220abbaab（）（）.21,abab（）22336xxyxyx；（）211,aaababaab2222222（）.ababbabbaabab3,xxyy（）2220abbaab（）（）.21,abab（）22336xxyxyx；（）211,aaababaab2222222（）.ababbabbaabab针对练习3.写出下列等式中所缺的分子或分母．(1)(2)(3)21()(0)cababc；22()()mababab；1.()()xxxy-bcma＋mbx－y21()(0)cababc；22()()mababab；1.()()xxxy-例2不改变分式的值，把下列各式的分子与分母的各项系数都化为整数.⑴⑵(0.015)100500(0.30.04)100304xxxx解：5(0.6)301850322112(0.7)305abababab(0.015)100500(0.30.04)100304xxxx5(0.6)301850322112(0.7)305abababab例3不改变分式的值，使下列分子与分母都不含“－”号：⑴=⑵=⑶=37ab103mn25xy25xy37ab103mn37ab103mn25xy25xy37ab103mn归纳知识分式的符号法则将分式、分子、分母的符号改变其中的任意两个，其结果不变..aaaabbbb.aaaabbbb例4不改变分式的值，使分子、分母的第一项系数不含“－”号xyxy.+（）（）xyxyxyxyxyxy解：xyxy.+（）（）xyxyxyxyxyxy针对练习1.(中考·丽水)分式可变形为()A．B.C．D.11x2.(中考·淄博)下列运算错误的是()A.B.1abba22（）（）0.55100.20.323abababab11x11x11x11x1abab-abbaabbaDD11x1abba22（）（）0.55100.20.323abababab11x11x11x11x1abab-abbaabba课堂小结类比分数分式分式的基本性质内容作用注意0AACAACCBBCBBC（）,.三同一不分子分母的各项系数化为整数分式的符号法则0AACAACCBBCBBC（）,.2.若x，y的值均扩大为原来的3倍，则下列分式的值保持不变的是()(1)1ab＝()ab2c(c≠0)；(2)ma－b＝()a2－b2(a≠－b)；(3)xx(x－y)＝1().课堂练习1.写出下列等式中所缺的分子或分母：bcma＋mbx－yDA.2＋xx－yB.2yx2C.2y33x2D.2y2(x－y)2(1)1ab＝()ab2c(c≠0)；(2)ma－b＝()a2－b2(a≠－b)；(3)xx(x－y)＝1().A.2＋xx－yB.2yx2C.2y33x2D.2y2(x－y)23.下列各式与分式ab相等的是()A．－abB．－－abC．a－bD．－－a－bB4.根据分式的基本性质，分式－aa－b可变形为()A．a－a－bB．aa＋bC．－aa－bD．－aa＋bC3.下列各式与分式ab相等的是()A．－abB．－－abC．a－bD．－－a－b4.根据分式的基本性质，分式－aa－b可变形为()A．a－a－bB．aa＋bC．－aa－bD．－aa＋b5.不改变分式的值，把下列各式的分子、分母中各项系数都化为整数，且使分子和分母不含公因式：(1)0.2x＋y0.02x－0.5y；解：0.2x＋y0.02x－0.5y＝(0.2x＋y)×50(0.02x－0.5y)×50＝10x＋50yx－25y；(2)13x＋14y12x－13y.解：13x＋14y12x－13y＝13x＋14y×1212x－13y×12＝4x＋3y6x－4y.(1)0.2x＋y0.02x－0.5y；解：0.2x＋y0.02x－0.5y＝(0.2x＋y)×50(0.02x－0.5y)×50＝10x＋50yx－25y；(2)13x＋14y12x－13y.解：13x＋14y12x－13y＝13x＋14y×1212x－13y×12＝4x＋3y6x－4y.7.已知x：y：z＝2：3：4，求x＋y＋zx－2y＋3z的值．解：∵x：y：z＝2：3：4，∴设x＝2m，y＝3m，z＝4m(m≠0)．∴x＋y＋zx－2y＋3z＝2m＋3m＋4m2m－6m＋12m＝9m8m＝98.7.已知x：y：z＝2：3：4，求x＋y＋zx－2y＋3z的值．解：∵x：y：z＝2：3：4，∴设x＝2m，y＝3m，z＝4m(m≠0)．∴x＋y＋zx－2y＋3z＝2m＋3m＋4m2m－6m＋12m＝9m8m＝98.