24-6-2-正多边形的性质-2022-2023学年九年级数学下册同步教学课件(沪科版)

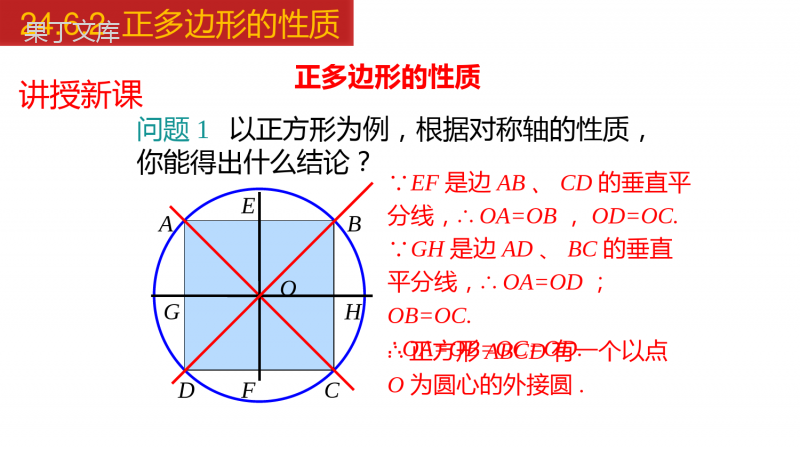
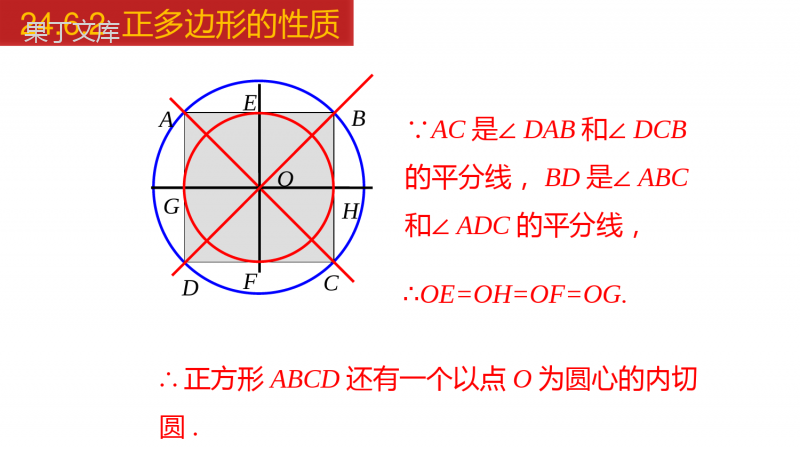
正多边形的性质24.6.2正多边形的性质学习目标1.理解正多边形的中心、半径、边心距、中心角的概念.2.掌握正多边形的性质并能加以应用.24.6.2正多边形的性质问题1什么是正多边形？问题2如何作出正多边形？各边相等，各角也相等的多边形叫做正多边形.将一个圆n等分，就可以作出这个圆的内接或外切正n边形.回顾复习24.6.2正多边形的性质讲授新课OABCD问题1以正方形为例，根据对称轴的性质，你能得出什么结论？EFGH∵EF是边AB、CD的垂直平分线，∴OA=OB，OD=OC.∵GH是边AD、BC的垂直平分线，∴OA=OD；OB=OC.∴OA=OB=OC=OD.∴正方形ABCD有一个以点O为圆心的外接圆.正多边形的性质24.6.2正多边形的性质OABCDEFGH∵AC是∠DAB和∠DCB的平分线，BD是∠ABC和∠ADC的平分线，∴OE=OH=OF=OG.∴正方形ABCD还有一个以点O为圆心的内切圆.24.6.2正多边形的性质所有的正多边形是不是都有一个外接圆和一个内切圆？想一想：任何正多边形都有一个外接圆和一个内切圆.24.6.2正多边形的性质OABCDEFGHRr360n知识要点正多边形每一条边所对的圆心角，叫做正多边形的中心角.正多边形的每个中心角都等于.内切圆的半径叫做正多边形的边心距.外接圆的半径叫做正多边形的半径.正多边形的外接圆和内切圆的公共圆心，叫做正多边形的中心.24.6.2正多边形的性质360n画出下列各正多边形的对称轴，看看能发现什么结果？24.6.2正多边形的性质要点精析：(1)正多边形都是轴对称图形，一个正n边形一共有n条对称轴，每一条对称轴都通过正多边形的中心.(2)当边数为偶数时，正多边形具有：轴对称性、中心对称性,它的中心就是对称中心.(3)当边数为奇数时，正多边形具有：轴对称性其中：对称轴条数与边数相等．24.6.2正多边形的性质如图，已知半径为4的圆内接正六边形ABCDEF：①它的中心角等于度；②OCBC(填＞、＜或＝）；③△OBC是三角形；④圆内接正六边形的面积是△OBC面积的倍.⑤圆内接正n边形面积公式：________________________.CDOBEFAP60=等边6正多边形的有关计算S正多边形=周长×边心距/224.6.2正多边形的性质求边长为a的正六边形的周长和面积.如图，过正六边形的中心O作OG⊥BC，垂足是G，连接OB，OC，设该正六边形的周长和面积分别为C和S.∵多边形ABCDEF是正六边形，∴∠BOC=60°，△BOC是等边三角形.∴C=6BC=6a.在△BOC中，有解：例133.22OGBCa==2133S=6BC.22OGa∴24.6.2正多边形的性质33.22OGBCa==2133S=6BC.22OGa∴例2一个上、下底面为全等正六边形的礼盒，高为10cm，上、下底面正六边形的边长为12cm，如果用彩色胶带按如图所示方式包扎礼盒，所需胶带长度至少为________________．(72360)cm24.6.2正多边形的性质(72360)cm胶带包括上、下面各3段，侧面6段．上、下面中的每段胶带长等于图中的OC的2倍．利用中心角可求得∠COB＝30°，由正六边形的边长为12cm，易得BC＝6cm，所以OB＝12cm，由勾股定理得OC＝cm，从而求得上、下面每段胶带长为cm，进而求出所需胶带的长度．2263OBBC123分析：24.6.2正多边形的性质2263OBBC123例3如图，AG是正八边形ABCDEFGH的一条对角线．（1）在剩余的顶点B、C、D、E、F、H中，连接两个顶点，使连接的线段与AG平行，并说明理由；（2）两边延长AB、CD、EF、GH，使延长线分别交于点P、Q、M、N，若AB=2，求四边形PQMN的面积．24.6.2正多边形的性质（1）在剩余的顶点B、C、D、E、F、H中，连接两个顶点，使连接的线段与AG平行，并说明理由；解：连接BF，CE，则有BF∥AG，CE∥AG．理由如下：∵ABCDEFGH是正八边形，∴它的内角都为135°．又∵HA=HG，∴∠HAG=22.5°.∴∠GAB=135°-1=112.5°∠．∴∠GAB=135°-1=112.5°∠．∵正八边形ABCDEFGH关于直线BF对称，即∠BAG+ABF=180°∠，故BFAG∥．1ABF=ABC=67.5.2∴∠∠同理，可得CE∥BF，∴CE∥AG；24.6.2正多边形的性质1ABF=ABC=67.5.2∴∠∠PNMQ（2）有题意可知∠PHA=PAH=45°∠，∴∠P=90°，同理可得∠Q=M=90°∠，∴四边形PQMN是矩形．∵∠PHA=PAH=QBC=QCB=MDE=MED=45°∠∠∠∠∠，AH=BC=DE，∴△PAH≌QCB△≌MDE△，∴PA=QB=QC=MD．即PQ=QM，故四边形PQMN是正方形．（2）两边延长AB、CD、EF、GH，使延长线分别交于点P、Q、M、N，若AB=2，求四边形PQMN的面积．24.6.2正多边形的性质在RtPA△H中，∵∠PAH=45°，AB=2，PA=ABsin452,∴PNMQPQ=PB+AB+BQ=2+22.∴故S四边形PQMN=22+22=1282.（）24.6.2正多边形的性质PA=ABsin452,∴PQ=PB+AB+BQ=2+22.∴22+22=1282.（）2.作边心距，构造直角三角形.1.连半径，得中心角；OABCDEFRMr·圆内接正多边形的辅助线方法归纳O边心距r边长一半半径RBM中心角一半24.6.2正多边形的性质如图,M,N分别是☉O内接正多边形AB,BC上的点,且BM=CN.(1)图①中∠MON=_______;图②中∠MON=;图③中∠MON=;(2)试探究∠MON的度数与正n边形的边数n的关系.ABCDEABCD.ABCMNMNMNOOO90°72°120°图①图②图③360MONn24.6.2正多边形的性质360MONn正多边形边数内角中心角外角346n60°120°120°90°90°90°120°60°60°360n°360n°1.完成下面的表格：(2)180nn-´°随堂练习24.6.2正多边形的性质360n°360n°(2)180nn-´°正多边形边数半径边长边心距周长面积34162332.填表：216333228422126324.6.2正多边形的性质23363332633.如图，已知半径为4的圆内接正六边形ABCDEF：①它的中心角等于度；②OCBC(填＞、＜或＝）；③△OBC是三角形；④圆内接正六边形的面积是△OBC面积的倍.CDOBEFAP60=等边64.若正多边形的边心距与半径的比为1∶2，则这个正多边形的边数是.424.6.2正多边形的性质5.如图，正五边形ABCDE内接于⊙O，则∠ADE的度数是（）A．60°B．45°C．36°D．30°·ABCDEOC24.6.2正多边形的性质6.如图，四边形ABCD是⊙O的内接正方形，若正方形的面积等于4，求⊙O的面积．解：∵正方形的面积等于4，sin452.AB=则半径为∴⊙O的面积为2π(2)2π.=∴正方形的边长AB=2.24.6.2正多边形的性质sin452.AB=2π(2)2π.=ABCDEFP7.如图，正六边形ABCDEF的边长为，点P为六边形内任一点，则点P到各边距离之和是多少？23∴点P到各边距离之和=3BD=3×6=18．解：过P作AB的垂线，分别交AB、DE于H、K，连接BD，作CGBD⊥于G.HK∴P到AF与CD的距离之和，及P到EF、BC的距离之和，均为HK的长.∵六边形ABCDEF是正六边形∴ABDE∥，AFCD∥，BCEF∥，∵BC=CD，∠BCD=ABC=CDE=120°∠∠，∴∠CBD=BDC=30°∠，BDHK∥，且BD=HK.∵CGBD⊥，∴BD=2BG=2×BC×cosCBD=∠6.G24.6.2正多边形的性质23课堂小结正多边形的性质正多边形的有关概念正多边形的有关计算添加辅助线的方法：连半径，作边心距中心半径边心距中心角正多边形的对称性24.6.2正多边形的性质THANKS“”24.6.2正多边形的性质