二次函数与一元二次方程(课件-含动画演示)-九年级数学上册同步精品课堂(人教版)

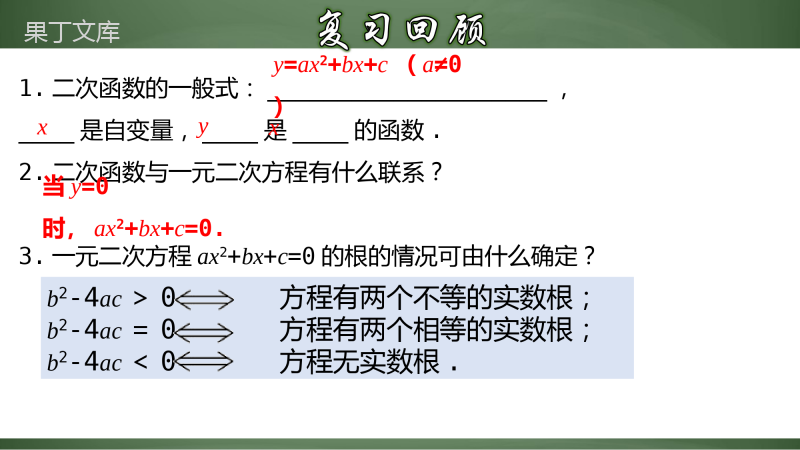
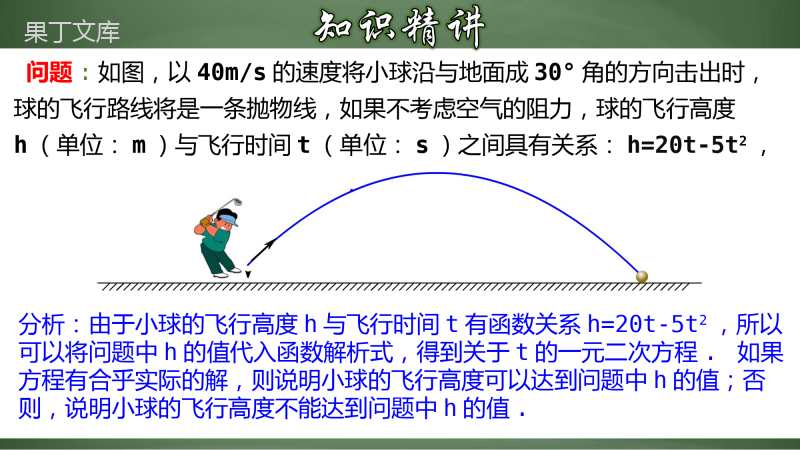
二次函数与一元二次方程1.通过探索，理解二次函数与一元二次方程(不等式）之间的联系.(难点）2.能运用二次函数及其图象、性质确定方程的解或不等式的解集.（重点）3.了解用图象法求一元二次方程的近似根.1.二次函数的一般式：____________________，____是自变量，____是____的函数.2.二次函数与一元二次方程有什么联系？3.一元二次方程ax2+bx+c=0的根的情况可由什么确定？当y=0时，ax2+bx+c=0.y=ax2+bx+c（a≠0）xyxb2-4ac＞0方程有两个不等的实数根；b2-4ac＝0方程有两个相等的实数根；b2-4ac＜0方程无实数根.问题:如图，以40m/s的速度将小球沿与地面成30°角的方向击出时，球的飞行路线将是一条抛物线，如果不考虑空气的阻力，球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有关系：h=20t-5t2，考虑以下问题：(1)小球的飞行高度能否达到15m？如果能，需要多少飞行时间？(2)小球的飞行高度能否达到20m？如果能，需要多少飞行时间？(3)小球的飞行高度能否达到20.5m？为什么？(4)小球从飞出到落地要用多少时间？问题:如图，以40m/s的速度将小球沿与地面成30°角的方向击出时，球的飞行路线将是一条抛物线，如果不考虑空气的阻力，球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有关系：h=20t-5t2，分析：由于小球的飞行高度h与飞行时间t有函数关系h=20t-5t2，所以可以将问题中h的值代入函数解析式，得到关于t的一元二次方程.如果方程有合乎实际的解，则说明小球的飞行高度可以达到问题中h的值；否则，说明小球的飞行高度不能达到问题中h的值.（1）小球的飞行高度能否达到15m？如果能，需要多少飞行时间？因此，当球飞行1s或3s时，它的飞行高度为15m.解：当h=15时，15=20t-5t2,整理得，t2-4t+3=0,解得，t1=1,t2=3.（2）小球的飞行高度能否达到20m？如果能，需要多少飞行时间？解：（2）当h=20时，20=20t-5t2,整理得，t2-4t+4=0,解得，t1=t2=2.因此，当小球飞行2s时，它的飞行高度为20m.（3）球的飞行高度能否达到20.5m？如果能，需要多少飞行时间？解：(3)当h=20.5时，20t-5t2=20.5整理得，t2-4t+4.1=0因为(-4)2-4×4.1=-0.4＜0，所以方程无实数根.这就是说，小球的飞行高度达不到20.5m.（4）球从飞出到落地要用多少时间？解：(4)小球飞出时和落地时的高度h都为0m，因此有20t-5t2=0整理得，t2-4t=0解得，t1=0，t2=4因此，当小球飞行0s和4s时，它的高度为0m.这表明小球从飞h=20t-5t220t-5t2=15，20t-5t2=20，20t-5t2=20.5，20t-5t2=0.从上面可以看出，二次函数与一元二次方程联系密切．例如，已知二次函数y=－x2＋4x的值为3，求自变量x的值，可以解一元二次方程－x2＋4x=3（即x2－4x+3=0）．反过来，解方程x2－4x+3=0又可以看作已知二次函数y=x2－4x+3的值为0，求自变量x的值．已知二次函数的值，求自变量x的值.解一元二次方程下列二次函数的图象与x轴有公共点吗？如果有，公共点的横坐标是多少？当x取公共点的横坐标时，函数值是多少？由此，你能得出相应的一元二次方程的根吗？(1)y=x2+x-2；(2)y=x2-6x+9；(3)y=x2-x+1.(1)抛物线y=x2+x-2与x轴有两个公共点，它们的横坐标是-2，1.当x取公共点的横坐标时，函数值是0.由此得出方程x2+x-2=0的根是-2，1.下列二次函数的图象与x轴有公共点吗？如果有，公共点的横坐标是多少？当x取公共点的横坐标时，函数值是多少？由此，你能得出相应的一元二次方程的根吗？(1)y=x2+x-2；(2)y=x2-6x+9；(3)y=x2-x+1.(2)抛物线y=x2-6x+9与x轴有一个公共点，这点的横坐标是3.当x=3时，函数值是0.由此得出方程x2-6x+9=0有两个相等的实数根3.下列二次函数的图象与x轴有公共点吗？如果有，公共点的横坐标是多少？当x取公共点的横坐标时，函数值是多少？由此，你能得出相应的一元二次方程的根吗？(1)y=x2+x-2；(2)y=x2-6x+9；(3)y=x2-x+1.(3)抛物线y=x2-x+1与x轴没有公共点.由此可知，方程x2-x+1=0没有实数根.反过来，由一元二次方程的根的情况，也可以确定相应的二次函数图象与x轴的位置关系.一般地，从二次函数y=ax2+bx+c的图象可得如下结论.(1)如果抛物线y=ax2+bx+c与x轴有公共点，公共点的横坐标是x0，那么当x=x0时，函数的值是0，因此x=x0就是方程ax2+bx+c=0的一个根.(2)二次函数y=ax2+bx+c的图象与x轴的位置关系有三种：没有公共点，有一个公共点，有两个公共点.这对应着一元二次方程ax2+bx+c=0的根的三种情况：没有实数根，有两个相等的实数根，有两个不等的实数根.例1.利用函数图象求方程x2-2x-2=0的实数根(结果保留小数点后一位).解：画出函数y=x2-2x-2的图象，它与x轴的公共点的横坐标大约是-0.7，2.7.所以方程x2-2x-2=0的实数根为x1≈-0.7，x2≈2.7我们还可以通过不断缩小根所在的范围估计一元二次方程的根.例2.已知关于x的二次函数y＝mx2－(m＋2)x＋2(m≠0)．(1)求证：此抛物线与x轴总有两个交点；(2)若此抛物线与x轴总有两个交点，且它们的横坐标都是整数，求正整数m的值．(1)证明：∵m≠0，∴Δ＝(m＋2)2－4m×2＝m2＋4m＋4－8m＝(m－2)2.∵(m－2)2≥0，∴Δ≥0，∴此抛物线与x轴总有两个交点；(2)解：令y＝0，则(x－1)(mx－2)＝0，所以x－1＝0或mx－2＝0，解得x1＝1，x2＝.当m为正整数1或2时，x2为整数，即抛物线与x轴总有两个交点，且它们的横坐标都是整数．所以正整数m的值为1或2.2m例2.已知关于x的二次函数y＝mx2－(m＋2)x＋2(m≠0)．(1)求证：此抛物线与x轴总有两个交点；(2)若此抛物线与x轴总有两个交点，且它们的横坐标都是整数，求正整数m的值．2m已知：抛物线y＝x2＋ax＋a－2.(1)求证：不论a取何值时，抛物线y＝x2＋ax＋a－2与x轴都有两个不同的交点；(2)设这个二次函数的图象与x轴相交于A(x1，0)，B(x2，0)，且x1、x2的平方和为3，求a的值．(1)证明：∵Δ＝a2－4(a－2)＝(a－2)2＋4＞0，∴不论a取何值时，抛物线y＝x2＋ax＋a－2与x轴都有两个不同的交点；(2)解：∵x1＋x2＝－a，x1·x2＝a－2，∴x12＋x22＝(x1＋x2)2－2x1·x2＝a2－2a＋4＝3，∴a＝1.例3.在二次函数y＝ax2+bx+c中，函数y与自变量x的部分对应值如表，则方程ax2+bx+c＝0的一个解x的范围是（）A．1＜x＜1.1B．1.1＜x＜1.2C．1.2＜x＜1.3D．1.3＜x＜1.4x…11.11.21.31.4…y…10.490.040.591.16…【分析】由表格中数据可知，当x＝1.1时，y＝－0.49.当x＝1.2时，y＝0.04于是可得，当y＝0时，相应的自变量x的取值范围为1.1＜x＜1.2故选BB根据下表的对应值，可判断关于x的一元二次方程必有一个根满足（）A．B．C．D．x…00.51……12.532.51…D例4.如图，一次函数y1＝kx+b与二次函数y2＝ax2交于A（﹣1，1）和B（2，4）两点，则当y1＞y2时x的取值范围是（）A．x＜﹣1B．x＞2C．﹣1＜x＜2D．x＜﹣1或x＞2【分析】从图象上找出两函数图象交点坐标，再根据两函数图象的上下位置关系，判断时，x的范围．【详解】解：已知函数图象的两个交点坐标分别为A和B两点，∴当时，有﹣1＜x＜2；C如图，抛物线与直线交于A、B两点，下列是关于x的不等式或方程，结论正确的是（）A．的解集是B．的解集是C．的解集是D．的解是或D例5.如图，丁丁在扔铅球时，铅球沿抛物线运行，其中x是铅球离初始位置的水平距离，y是铅球离地面的高度.（1）当铅球离地面的高度为2.1m时，它离初始位置的水平距离是多少？（2）铅球离地面的高度能否达到2.5m，它离初始位置的水平距离是多少？（3）铅球离地面的高度能否达到3m？为什么？268-10105xyx268-10105xyx解（1）由抛物线的表达式得即解得即当铅球离地面的高度为2.1m时，它离初始位置的水平距离是1m或5m.2682.1-10105xx2650xx12=1=5.xx，（1）当铅球离地面的高度为2.1m时，它离初始位置的水平距离是多少？2682.1-10105xx2650xx12=1=5.xx，（2）铅球离地面的高度能否达到2.5m，它离初始位置的水平距离是多少？（2）由抛物线的表达式得即解得即当铅球离地面的高度为2.5m时，它离初始位置的水平距离是3m.2682.5-10105xx2690xx12==3.xx2682.5-10105xx2690xx12==3.xx（3）由抛物线的表达式得即因为所以方程无实根.所以铅球离地面的高度不能达到3m.2683-10105xx26140xx2=-6-41140（），（3）铅球离地面的高度能否达到3m？为什么？2683-10105xx26140xx2=-6-41140（），1．如图，抛物线的对称轴是，关于x的方程的一个根为，则另一个根为（）A．B．C．D．0C2．若二次函数的图象与坐标轴有三个交点，则m的取值范围是（）A．且B．且C．D．A3．已知二次函数y=-x2+2x+m的部分图像如图所示，则关于的一元二次方程-x2+2x+m=0的解为______________．，4．根据下表的对应值，可判断关于x的一元二次方程必有一个根满足（）A．B．C．D．x…00.51……12.532.51…D5．已知二次函数的图像的顶点为，与x轴交于点，根据图像回答下列问题：当x_______时，y随x的增大而减小：方程的两个根是_______________．＜2，6．如图，一次函数的图像与二次函数的图像相交于点，则解集是___________．−?