中考数学专题复习课件：几何类比拓展探究题

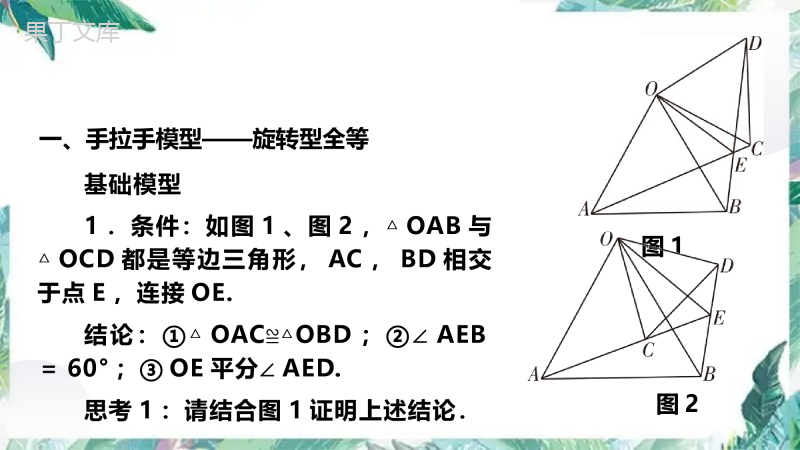
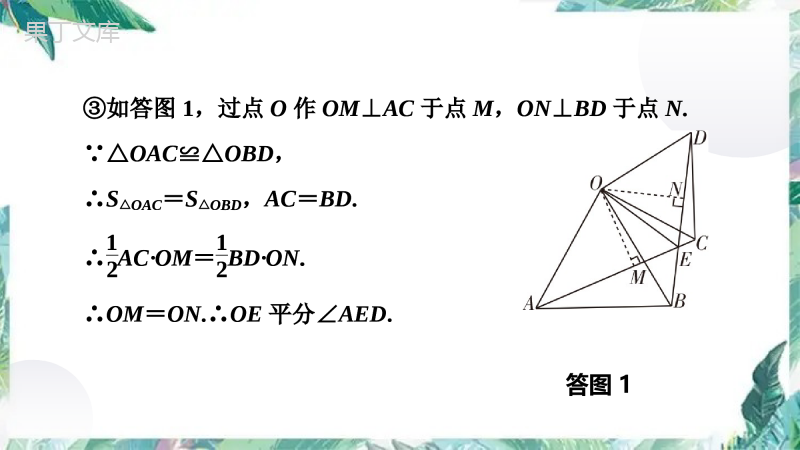
中考数学专题复习几何类比拓展探究题基础模型1．条件：如图1、图2，△OAB与△OCD都是等边三角形，AC，BD相交于点E，连接OE.结论：①△OAC≌△OBD；②∠AEB＝60°；③OE平分∠AED.思考1：请结合图1证明上述结论．一、手拉手模型——旋转型全等图1图2证明：①∵△OAB与△OCD都是等边三角形，∴OA＝OB，OC＝OD，∠AOB＝∠COD＝60°.∴∠AOB＋∠BOC＝∠COD＋∠BOC，即∠AOC＝∠BOD.∴△OAC≌△OBD(SAS)．②∵△OAC≌△OBD，∴∠OAC＝∠OBD.∵△OAB是等边三角形，∴∠OAB＋∠OBA＝60°＋60°＝120°.∴∠OAC＋∠BAE＋∠OBA＝120°.∴∠OBD＋∠BAE＋∠OBA＝120°，即∠EAB＋∠EBA＝120°.∴∠AEB＝180°－120°＝60°.③如答图1，过点O作OM⊥AC于点M，ON⊥BD于点N.∵△OAC≌△OBD，∴S△OAC＝S△OBD，AC＝BD.∴12AC·OM＝12BD·ON.∴OM＝ON.∴OE平分∠AED.答图1③如答图1，过点O作OM⊥AC于点M，ON⊥BD于点N.∵△OAC≌△OBD，∴S△OAC＝S△OBD，AC＝BD.∴12AC·OM＝12BD·ON.∴OM＝ON.∴OE平分∠AED.模型推广1．条件：如图3、图4，△OAB与△OCD都是等腰直角三角形，∠AOB＝∠COD＝90°，AC，BD相交于点E，连接OE.结论：①△OAC≌△OBD；②∠AEB＝90°；③OE平分∠AED.图3图42．条件：如图5、图6，△OAB与△OCD都是等腰三角形，OA＝OB，OC＝OD，∠AOB＝∠COD，AC，BD相交于点E，连接OE.结论：①△OAC≌△OBD；②∠AEB＝∠AOB；③OE平分∠AED.图5图63．条件：如图7，正方形ABCD和正方形AEFG，连接DG，BE交于点M，连接AM，过点A作AH⊥DG，AK⊥BE.结论：①△DAG≌△BAE；②∠DME＝∠DAB＝90°；③AM平分∠DME；④四边形AHMK是正方形．图74．条件：如图8，正五边形ABCDE和正五边形AB1C1D1E1，BB1，EE1相交于点O，连接AO.结论：①△ABB1≌△AEE1；②∠BOE＝∠BAE；③AO平分∠BOE1.图8注意：(1)该模型可推广到任意正n边形，利用正n边形的性质将其转化为模型推广2即可．(2)等边三角形(图1)→等腰直角三角形(图3)→一般等腰三角形(图5)→正n边形为图形形状变化引起的探究．5．条件：如图9、图10，△OAB和△OCD都是等腰直角三角形，∠AOB＝∠COD＝90°，连接AD，BC，点E，M，N分别是边AB，AD，BC的中点，连接EM，EN，MN.结论：①EM＝EN；②∠MEN＝∠AOB＝90°；③△EMN是等腰直角三角形．注意：当△OAB和△OCD都是等边三角形时，△EMN是等边三角形．图9图106．条件：如图11，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，连接CD，BE，点F是BE的中点，连接AF.结论：①CD＝2AF；②S△ABE＝S△ACD.图11【提示】①如图12，延长AF到点G，使得FG＝AF，连接BG，GE，可证△CAD≌△ABG，从而CD＝AG＝2AF.②如图13，作DN⊥AC于点N，EM⊥BA的延长线于点M，可证△ADN≌△AEM，从而S△ABE＝S△ACD.图12图13二、手拉手模型——旋转型相似基础模型2．条件：如图14，在△AOB中，CD∥AB，将△OCD绕点O旋转到如图15所示的位置，AC与BD所在直线相交于点E，与OB相交于点F.结论：①△OAC∽△OBD；②∠AEB＝∠AOB.思考2：请结合图15证明上述结论．图14图15证明：①在△OAB中，CD∥AB，∴△OCD∽△OAB.∴OCOA＝ODOB.∴OAOB＝OCOD.∵∠AOB＝∠COD，∴∠AOB－∠COB＝∠COD－∠COB.∴∠AOC＝∠BOD.又OAOB＝OCOD，∴△OAC∽△OBD.证明：①在△OAB中，CD∥AB，∴△OCD∽△OAB.∴OCOA＝ODOB.∴OAOB＝OCOD.∵∠AOB＝∠COD，∴∠AOB－∠COB＝∠COD－∠COB.∴∠AOC＝∠BOD.又OAOB＝OCOD，∴△OAC∽△OBD.②∵△OAC∽△OBD，∴∠OAC＝∠OBD.在△AOF与△EFB中，∠OFA＝∠EFB，∴∠AOF＝∠BEF，即∠AEB＝∠AOB.模型推广1．条件：如图16，∠AOB＝90°，CD∥AB，将△OCD绕点O旋转到如图17所示的位置，连接AC，BD相交于点E，连接AD，BC.图16图17结论：①△OAC∽△OBD；②AC⊥BD；③BDAC＝tan∠OAB；④AD2＋BC2＝AB2＋CD2.【提示】①②证明过程同基础模型2，③可由①利用相似三角形的性质证得，④可由②利用勾股定理证得．结论：①△OAC∽△OBD；②AC⊥BD；③BDAC＝tan∠OAB；④AD2＋BC2＝AB2＋CD2.2．条件：如图18，△OAB是等腰三角形，AO＝AB，CD∥AB，将△OCD绕点O旋转到如图19所示的位置，连接AC，BD，延长BD与AC交于点E.图18图19结论：①△OAC∽△OBD；②BDAC＝OBOA；③∠AEB＝∠AOB＝∠COD.结论：①△OAC∽△OBD；②BDAC＝OBOA；③∠AEB＝∠AOB＝∠COD.三、一线三等角模型基础模型3．条件：如图20，已知∠1＝∠2＝∠3＝60°.结论：①△ABC∽△CDE；②AB·DE＝BC·CD.思考3：请结合图20证明上述结论．图20证明：①∵∠ACD＝∠1＋∠BAC＝∠2＋∠DCE，∴∠BAC＝∠DCE.又∠1＝∠3，∴△ABC∽△CDE.②∵△ABC∽△CDE，∴ABCD＝BCDE.∴AB·DE＝BC·CD.证明：①∵∠ACD＝∠1＋∠BAC＝∠2＋∠DCE，∴∠BAC＝∠DCE.又∠1＝∠3，∴△ABC∽△CDE.②∵△ABC∽△CDE，∴ABCD＝BCDE.∴AB·DE＝BC·CD.模型推广1．条件：如图21，已知∠1＝∠2＝∠3.结论：①△ABC∽△CDE；②AB·DE＝BC·CD.2．条件：如图22，已知∠1＝∠2＝∠3＝90°.结论：①△ABC∽△CDE；②AB·DE＝BC·CD.图21图223．条件：如图23、图24，已知△ABC为等腰直角三角形，AB＝AC，∠BAC＝90°，过点A的直线l绕点A旋转，分别过点B，C向直线l作垂线，垂足为E，D.结论：①△ABE≌△CAD；②如图23，DE＋BE＝CD；③如图24，CD＋BE＝DE.图23图24四、对角互补模型基础模型4．条件：∠AOB＝∠DCE＝90°，OC平分∠AOB.结论：如图25，①CD＝CE；②OE＋OD＝2OC；③S△COE＋S△CDO＝12OC2.图25结论：如图25，①CD＝CE；②OE＋OD＝2OC；③S△COE＋S△CDO＝12OC2.如图26，①CD＝CE；②OE－OD＝2OC；③S△COE－S△CDO＝12OC2.思考4：结合图25证明上述结论．图26图25如图26，①CD＝CE；②OE－OD＝2OC；③S△COE－S△CDO＝12OC2.思考4：结合图25证明上述结论．证明：①如答图2，过点C作CG⊥OE于点G，CF⊥OA于点F.∵∠AOB＝90°，∴四边形OGCF是矩形．∴∠FCG＝90°，∠CGE＝180°－∠OGC＝90°＝∠CFD.∵OC平分∠AOB，∴CF＝CG.∴四边OGCF是正方形．∵∠FCG＝∠DCE＝90°，∴∠FCD＝∠GCE＝90°－∠OCG.又∠CFD＝∠CGE，∴△FCD≌△GCE(ASA)．∴CD＝CE.答图2②∵△FCD≌△GCE，∴FD＝GE.∴OE＋OD＝OG＋GE＋OD＝OG＋FD＋OD＝OG＋OF＝2OC.③∵△FCD≌△GCE，∴S△FCD＝S△GCE.∴S△COE＋S△CDO＝S△COG＋S△GCE＋S△CDO＝S△COG＋S△FCD＋S△CDO＝S四边形OGCF＝OG2＝12OC2.②∵△FCD≌△GCE，∴FD＝GE.∴OE＋OD＝OG＋GE＋OD＝OG＋FD＋OD＝OG＋OF＝2OC.③∵△FCD≌△GCE，∴S△FCD＝S△GCE.∴S△COE＋S△CDO＝S△COG＋S△GCE＋S△CDO＝S△COG＋S△FCD＋S△CDO＝S四边形OGCF＝OG2＝12OC2.模型推广1．条件：∠AOB＝60°，∠DCE＝120°，OC平分∠AOB.结论：如图27，①CD＝CE；②OE＋OD＝3OC；③S△COE＋S△CDO＝34OC2.如图28，①CD＝CE；②OE－OD＝3OC；③S△COE－S△CDO＝34OC2.图27图28结论：如图27，①CD＝CE；②OE＋OD＝3OC；③S△COE＋S△CDO＝34OC2.如图28，①CD＝CE；②OE－OD＝3OC；③S△COE－S△CDO＝34OC2.2．条件：∠AOB＝2α，∠DCE＝180°－2α，OC平分∠AOB.结论：如图29，①CD＝CE；②OE＋OD＝2OC·cosα；③S△COE＋S△CDO＝OC2·sinα·cosα.如图30，①CD＝CE；②OE－OD＝2OC·cosα；③S△COE－S△CDO＝OC2·sinα·cosα.注意：若将CD＝CE变为条件，OC平分∠AOB变为结论，所有结论依然成立．图29图30五、半角模型基础模型5．条件：在正方形ABCD中，∠EAF＝45°，AE交直线BC于点E，AF交直线DC于点F，AE，AF分别交直线BD于点M，N，连接NE，EF.结论：如图31，①BE＋DF＝EF；②△ANE是等腰直角三角形；③EF＝2MN.图31结论：如图31，①BE＋DF＝EF；②△ANE是等腰直角三角形；③EF＝2MN.如图32，①DF－BE＝EF；②△ANE是等腰直角三角形；③EF＝2MN.思考5：结合图31证明上述结论．图32如图32，①DF－BE＝EF；②△ANE是等腰直角三角形；③EF＝2MN.思考5：结合图31证明上述结论．证明：①如答图3，过点A作AG⊥AF，交CB的延长线于点G，则∠GAB＋∠BAF＝∠GAF＝90°.∵四边形ABCD是正方形，∴AB＝AD，∠ABG＝∠BAD＝∠ADF＝90°.∴∠BAF＋∠FAD＝90°.∴∠GAB＝∠FAD.∴△AGB≌△AFD(ASA)．∴BG＝DF，AG＝AF.∵∠EAF＝45°，∴∠GAE＝90°－∠EAF＝45°＝∠EAF.∵AE＝AE，∴△GAE≌△FAE.∴EG＝EF.答图3②∵四边形ABCD是正方形，∴∠MBA＝∠MBN＝45°.在△AMN和△BME中，∠MAN＝∠MBE＝45°，∠AMN＝∠BME，∴△AMN∽△BME.∴AMBM＝MNME.∴AMMN＝BMME，即AMNM＝MBME.∵∠AMB＝∠NME，∴△AMB∽△NME.∴∠MEN＝∠MBA＝45°.∵∠EAF＝45°，∴∠ANE＝90°.∴△ANE是等腰直角三角形．②∵四边形ABCD是正方形，∴∠MBA＝∠MBN＝45°.在△AMN和△BME中，∠MAN＝∠MBE＝45°，∠AMN＝∠BME，∴△AMN∽△BME.∴AMBM＝MNME.∴AMMN＝BMME，即AMNM＝MBME.∵∠AMB＝∠NME，∴△AMB∽△NME.∴∠MEN＝∠MBA＝45°.∵∠EAF＝45°，∴∠ANE＝90°.∴△ANE是等腰直角三角形．③∵△ANE是等腰直角三角形，∴AE＝2AN.∵△GAE≌△FAE，∴∠BEM＝∠AEF.∵△AMN∽△BME，∴∠BEM＝∠ANM.∴∠ANM＝∠AEF.又∠MAN＝∠FAE，∴△AMN∽△AFE.∴MNFE＝ANAE＝12.∴EF＝2MN.③∵△ANE是等腰直角三角形，∴AE＝2AN.∵△GAE≌△FAE，∴∠BEM＝∠AEF.∵△AMN∽△BME，∴∠BEM＝∠ANM.∴∠ANM＝∠AEF.又∠MAN＝∠FAE，∴△AMN∽△AFE.∴MNFE＝ANAE＝12.∴EF＝2MN.模型推广1．条件：如图33、图34，在等腰直角三角形ABC中，∠BAC＝90°，∠EAD＝45°.AE交直线BC于点E，AD交直线BC于点D.结论：BD2＋CE2＝DE2.图33图34例1如图1，在矩形ABCD中(BC>AB)，点P是线段BC上一动点，连接AP，并将线段AP绕点A逆时针旋转90°得到线段AE，连接EP，ED，延长ED交BC的延长线于点F，延长DE交BA的延长线于点Q.(1)在图1中，∠EAQ______∠APB；(填典例分析动点探究类型1＝图1(2)如图2，若AP∥DE，写出三个与∠EAQ相等的角；解：∠QDA，∠F，∠BPA，∠DAP(写三个即可)图2(3)如图3，若AB＝1，BC＝2，AP∥DE，求证：四边形APEQ是平行四边形；图3证明：∵AP∥DE，∠EAP＝90°，且四边形ABCD是矩形，∴∠AED＝∠ADC＝∠DCF＝90°，AD∥BF，CD＝AB＝1，AD＝BC＝2.∴∠EAD＋∠ADE＝∠ADE＋∠CDF＝90°.∴∠EAD＝∠CDF.∴△EAD∽△CDF.∴AEDC＝ADDF.∵AP∥DE，AD∥BF，∴四边形DAPF是平行四边形．∴AP＝DF.证明：∵AP∥DE，∠EAP＝90°，且四边形ABCD是矩形，∴∠AED＝∠ADC＝∠DCF＝90°，AD∥BF，CD＝AB＝1，AD＝BC＝2.∴∠EAD＋∠ADE＝∠ADE＋∠CDF＝90°.∴∠EAD＝∠CDF.∴△EAD∽△CDF.∴AEDC＝ADDF.∵AP∥DE，AD∥BF，∴四边形DAPF是平行四边形．∴AP＝DF.∵AP＝AE，∴AE＝DF，∠APE＝∠AEP＝45°.设AE＝DF＝x，则x1＝2x.∴x＝2(负值舍去)．∵AB＝1，AP＝2，∴PB＝1.∴∠PAB＝45°＝∠APE.∴AQ∥PE.∴四边形APEQ是平行四边形．∵AP＝AE，∴AE＝DF，∠APE＝∠AEP＝45°.设AE＝DF＝x，则x1＝2x.∴x＝2(负值舍去)．∵AB＝1，AP＝2，∴PB＝1.∴∠PAB＝45°＝∠APE.∴AQ∥PE.∴四边形APEQ是平行四边形．(4)如图4，若AB＝1，BC＝n2＋1(n为正数)，且AP∥DE.①求EP的值；(用含n的代数式表示)②求BCBP的最小值．图4(4)如图4，若AB＝1，BC＝n2＋1(n为正数)，且AP∥DE.①求EP的值；(用含n的代数式表示)②求BCBP的最小值．解：①∵四边形ABCD是矩形，AB＝1，BC＝n2＋1，∴AD＝BC＝n2＋1，DC＝AB＝1.同(3)可得△EAD∽△CDF，由(3)可知四边形DAPF是平行四边形，∴AP＝DF.又∵AP＝AE，∴AE＝DF.设AE＝x.∵△EAD∽△CDF，∴AEDC＝ADDF.∴AE1＝n2＋1AE.∴AE＝n2＋1.解：①∵四边形ABCD是矩形，AB＝1，BC＝n2＋1，∴AD＝BC＝n2＋1，DC＝AB＝1.同(3)可得△EAD∽△CDF，由(3)可知四边形DAPF是平行四边形，∴AP＝DF.又∵AP＝AE，∴AE＝DF.设AE＝x.∵△EAD∽△CDF，∴AEDC＝ADDF.∴AE1＝n2＋1AE.∴AE＝n2＋1.在Rt△PAE中，AP＝AE，∴EP＝2n2＋2.②在Rt△ABP中，AP＝AE＝n2＋1，AB＝1，∴BP＝AP2－AB2＝n.∴BCBP＝n2＋1n＝n＋1n＝(n)2＋1n2－2＋2＝n－1n2＋2≥2.∴BCBP的最小值为2.在Rt△PAE中，AP＝AE，∴EP＝2n2＋2.②在Rt△ABP中，AP＝AE＝n2＋1，AB＝1，∴BP＝AP2－AB2＝n.∴BCBP＝n2＋1n＝n＋1n＝(n)2＋1n2－2＋2＝n－1n2＋2≥2.∴BCBP的最小值为2.训练1.(2020济南)在等腰三角形ABC中，AC＝BC，△ADE是直角三角形，∠DAE＝90°，∠ADE＝12∠ACB，连接BD，BE，点F是BD的中点，连接CF.(1)当∠CAB＝45°时．①如图1，当顶点D在边AC上时，请直接写出∠EAB与∠CBA的数量关系是________________.线段BE与线段CF的数量关系是____________；∠EAB＝∠CBA图1CF＝12BE训练1.(2020济南)在等腰三角形ABC中，AC＝BC，△ADE是直角三角形，∠DAE＝90°，∠ADE＝12∠ACB，连接BD，BE，点F是BD的中点，连接CF.(1)当∠CAB＝45°时．①如图1，当顶点D在边AC上时，请直接写出∠EAB与∠CBA的数量关系是________________.线段BE与线段CF的数量关系是____________；CF＝12BE②如图2，当顶点D在边AB上时，(1)中线段BE与线段CF的数量关系是否仍然成立？若成立，请给予证明，若不成立，请说明理由；学生经过讨论，探究出以下解决问题的思路，仅供大家参考：思路一：作等腰三角形ABC底边上的高CM，并取BE的中点N，再利用三角形全等或相似有关知识来解决问题；思路二：取DE的中点G，连接AG，CG，并把△CAG绕点C逆时针旋转90°，再利用旋转性质、三角形全等或相似有关知识来解决问题．图2解：(1)②结论仍然成立．答图4证明：如答图4，过点C作CM⊥AB于点M，延长CM交BE于点N，连接FN，则∠CMF＝∠BMN＝90°.∵AC＝BC，∠CAB＝45°，∴∠ACB＝90°.∴∠ADE＝45°，AM＝CM＝BM.∵∠DAE＝90°＝∠BMN，∴MN∥AE.∴MN＝BN.又点F是BD的中点，∴DE∥FN.∴∠MFN＝∠ADE＝45°.∴MF＝MN.∴△CMF≌△BMN(SAS)．∴CF＝BN＝MN.∴CF＝12BE.又点F是BD的中点，∴DE∥FN.∴∠MFN＝∠ADE＝45°.∴MF＝MN.∴△CMF≌△BMN(SAS)．∴CF＝BN＝MN.∴CF＝12BE.(2)当∠CAB＝30°时，如图3，当顶点D在边AC上时，写出线段BE与线段CF的数量关系，并说明理由．图3解：结论：BE＝23CF.理由：如答图5，过点C作CT⊥AB于点T，连接TF，则∠CTB＝90°.答图5∵CA＝CB，∠CAB＝30°，CT⊥AB，∴AT＝TB＝3CT，∠CBA＝∠CAB＝30°.∴AB＝23CT，∠ACB＝120°.∴∠ADE＝60°.∵点F是BD的中点，∴TF∥AD，AD＝2FT.解：结论：BE＝23CF.理由：如答图5，过点C作CT⊥AB于点T，连接TF，则∠CTB＝90°.∵CA＝CB，∠CAB＝30°，CT⊥AB，∴AT＝TB＝3CT，∠CBA＝∠CAB＝30°.∴AB＝23CT，∠ACB＝120°.∴∠ADE＝60°.∵点F是BD的中点，∴TF∥AD，AD＝2FT.∴∠FTB＝∠CAB＝30°.∵∠CTB＝∠DAE＝90°，∴∠CTF＝∠BAE＝60°.∵∠ADE＝60°，∴AE＝3AD＝23FT.∴ABTC＝AETF＝23.∴△BAE∽△CTF.∴BECF＝BACT＝23.∴BE＝23CF.∴∠FTB＝∠CAB＝30°.∵∠CTB＝∠DAE＝90°，∴∠CTF＝∠BAE＝60°.∵∠ADE＝60°，∴AE＝3AD＝23FT.∴ABTC＝AETF＝23.∴△BAE∽△CTF.∴BECF＝BACT＝23.∴BE＝23CF.2．(1)【方法导引】问题：如图1，等边三角形ABC的边长为6，点O是∠ABC和∠ACB的平分线的交点，∠FOG＝120°，绕点O任意旋转∠FOG，分别交△ABC的两边于D，E两点，求四边形ODBE的面积．图1讨论：①小明：在∠FOG的旋转过程中，当OF经过点B时，OG一定经过点C.②小颖：小明的分析有道理，这样，我们就可以利用“ASA”证出△ODB≌△OEC.③小飞：因为△ODB≌△OEC，所以只要算出△OBC的面积就得出了四边形ODBE的面积．老师：同学们的思路很清晰，也很正确，在分析和解决问题时，我们经常会借用特例作辅助线来解决一般问题．请你按照讨论的思路，直接写出四边形ODBE的面积：_______.3333(2)【应用方法】①特例：如图2，∠FOG的顶点O在等边三角形ABC的边BC上，OB＝2，OC＝4，边OG⊥AC于点E，OF⊥AB于点D，求△BOD的面积．图2解：(2)①∵△ABC是等边三角形，∠B＝60°，OF⊥AB，∴∠BOD＝30°.∵OB＝2，∴BD＝1.∴OD＝OB2－OD2＝3.∴△BOD的面积为12BD·OD＝12×1×3＝32.解：(2)①∵△ABC是等边三角形，∠B＝60°，OF⊥AB，∴∠BOD＝30°.∵OB＝2，∴BD＝1.∴OD＝OB2－OD2＝3.∴△BOD的面积为12BD·OD＝12×1×3＝32.②探究：如图3，已知∠FOG＝60°，顶点O在等边三角形ABC的边BC上，OB＝2，OC＝4，记△BOD的面积为x，△COE的面积为y，求xy的值．解：如答图6，过点O作OM⊥AB于点M，ON⊥AC于点N.图3答图6由①得OM＝3，同理可得ON＝23.∵△ABC是等边三角形，∴∠B＝∠C＝60°.∵∠DOC＝∠B＋∠BDO＝∠FOG＋∠COE，且∠FOG＝60°，∴∠BDO＝∠COE.∴△BDO∽△COE.∴OBEC＝BDCO.∴BD·EC＝OB·OC＝2×4＝8.∴xy＝12BD·OM·12EC·ON＝12BD×3×12EC×23＝12.由①得OM＝3，同理可得ON＝23.∵△ABC是等边三角形，∴∠B＝∠C＝60°.∵∠DOC＝∠B＋∠BDO＝∠FOG＋∠COE，且∠FOG＝60°，∴∠BDO＝∠COE.∴△BDO∽△COE.∴OBEC＝BDCO.∴BD·EC＝OB·OC＝2×4＝8.∴xy＝12BD·OM·12EC·ON＝12BD×3×12EC×23＝12.③应用：如图4，已知∠FOG＝60°，顶点O在等边三角形ABC的边CB的延长线上，OB＝2，BC＝6，记△BOD的面积为a，△COE的面积为b，请直接写出a与b的关系式．解：ab＝48.图43.综合与实践【操作发现】如图1、图2，已知点P为正方形ABCD的边AD和CD上的一个动点(点A，D，C除外)，作射线BP，作AE⊥BP于点E，CF⊥BP于点F，DG⊥BP于点G.(1)如图1，当点P在CD上(点C，D除外)运动时，求证：AE＝CF＋图1图2(1)证明：如答图7，过点D作DH⊥CF交CF的延长线于点H，则∠CHD＝90°.∵四边形ABCD为正方形，∴AB＝CD，AB∥CD.∴∠ABE＝∠CPF.∵AE⊥BP，CF⊥BP，DG⊥BP，∴∠AEB＝∠HFP＝∠DGF＝90°＝∠CHD.答图7∴四边形HFGD为矩形，FG∥HD.∴HF＝DG，∠CDH＝∠CPF.∴∠ABE＝∠CDH.在△ABE和△CDH中，∠AEB＝∠CHD，∠ABE＝∠CDH，AB＝CD，∴△ABE≌△CDH(AAS)．∴AE＝CH＝CF＋HF＝CF＋DG.∴四边形HFGD为矩形，FG∥HD.∴HF＝DG，∠CDH＝∠CPF.∴∠ABE＝∠CDH.在△ABE和△CDH中，∠AEB＝∠CHD，∠ABE＝∠CDH，AB＝CD，∴△ABE≌△CDH(AAS)．∴AE＝CH＝CF＋HF＝CF＋DG.(2)如图2，当点P在AD上(点A，D除外)运动时，请直接写出线段AE，CF，DG之间的数量关系；解：线段AE，CF，DG之间的数量关系是CF＝AE＋DG.图2【拓广探索】(3)在(1)的条件下，找出与DG相等的线段，并说明理由；解：与DG相等的线段是EF.理由如下：∵四边形ABCD为正方形，∴AB＝BC，∠ABC＝90°.∵AE⊥BP，CF⊥BP，∴∠AEB＝∠BFC＝90°.∴∠ABE＋∠BAE＝∠ABE＋∠CBF＝90°.∴∠BAE＝∠CBF.在△ABE和△BCF中，∠AEB＝∠BFC，∠BAE＝∠CBF，AB＝BC，∴△ABE≌△BCF(AAS)．∴AE＝BF，BE＝CF.∴AE＝BF＝BE＋EF＝CF＋EF.由(1)得AE＝CF＋DG.∴DG＝EF.在△ABE和△BCF中，∠AEB＝∠BFC，∠BAE＝∠CBF，AB＝BC，∴△ABE≌△BCF(AAS)．∴AE＝BF，BE＝CF.∴AE＝BF＝BE＋EF＝CF＋EF.由(1)得AE＝CF＋DG.∴DG＝EF.(4)如图3，若点P为矩形ABCD的边CD上一点，作射线BP，作AE⊥BP于点E，CF⊥BP于点F，DG⊥BP于点G.若CD＝2BE＝6，EG＝43，求DG的长．图3(4)如图3，若点P为矩形ABCD的边CD上一点，作射线BP，作AE⊥BP于点E，CF⊥BP于点F，DG⊥BP于点G.若CD＝2BE＝6，EG＝43，求DG的长．解：如答图8，过点D作DQ⊥CF交CF的延长线于点Q.∵AE⊥BP，DH⊥CF，CF⊥BP，DG⊥BP，∴∠AEB＝∠CQD＝∠QFG＝∠DGF＝90°.∴四边形QFGD为矩形．∴QF＝DG，DQ＝FG.在矩形ABCD中，AB＝CD＝2BE＝6，∴BE＝3.答图8∴∠BAE＝30°.∴AE＝AB2－BE2＝33，∠ABE＝60°.同(1)可得△ABE≌△CDQ，∴BE＝DQ，AE＝CQ＝33.∴BE＝FG.∴BF＝EG＝43.∵∠ABC＝90°，∴∠CBF＝90°－∠ABE＝30°.∴CF＝BF·tan30°＝43×33＝4.∴DG＝QF＝CQ－CF＝33－4.∴∠BAE＝30°.∴AE＝AB2－BE2＝33，∠ABE＝60°.同(1)可得△ABE≌△CDQ，∴BE＝DQ，AE＝CQ＝33.∴BE＝FG.∴BF＝EG＝43.∵∠ABC＝90°，∴∠CBF＝90°－∠ABE＝30°.∴CF＝BF·tan30°＝43×33＝4.∴DG＝QF＝CQ－CF＝33－4.例2(2020河南)将正方形ABCD的边AB绕点A逆时针旋转至AB′，记旋转角为α，连接BB′，过点D作DE垂直于直线BB′，垂足为点E，连接DB′，CE.(1)如图1，当α＝60°时，△DEB′的形状为__________________，连接BD，可求出BB′CE的值为______；变换探究类型2等腰直角三角形例2题图12例2(2020河南)将正方形ABCD的边AB绕点A逆时针旋转至AB′，记旋转角为α，连接BB′，过点D作DE垂直于直线BB′，垂足为点E，连接DB′，CE.(1)如图1，当α＝60°时，△DEB′的形状为__________________，连接BD，可求出BB′CE的值为______；2(2)当0°＜α＜360°且α≠90°时，①(1)中的两个结论是否仍然成立？如果成立，请仅就图2的情形进行证明；如果不成立，请说明理由；②当以点B′，E，C，D为顶点的四边形是平行四边形时，请直接写出BEB′E的值．例2题图2(2)当0°＜α＜360°且α≠90°时，①(1)中的两个结论是否仍然成立？如果成立，请仅就图2的情形进行证明；如果不成立，请说明理由；②当以点B′，E，C，D为顶点的四边形是平行四边形时，请直接写出BEB′E的值．解：(2)①(1)中的两个结论仍然成立．证明：如答图9，连接BD，∵AB＝AB′，∠BAB′＝α，∴∠AB′B＝90°－α2.∵∠B′AD＝α－90°，AD＝AB′，∴∠AB′D＝135°－α2.∴∠EB′D＝∠AB′D－∠AB′B＝135°－α2－90°－α2＝45°.∵DE⊥BB′，∴∠EDB′＝45°＝∠EB′D.∴△DEB′是等腰直角三角形．∴DB′DE＝2.答图9证明：如答图9，连接BD，∵AB＝AB′，∠BAB′＝α，∴∠AB′B＝90°－α2.∵∠B′AD＝α－90°，AD＝AB′，∴∠AB′D＝135°－α2.∴∠EB′D＝∠AB′D－∠AB′B＝135°－α2－90°－α2＝45°.∵DE⊥BB′，∴∠EDB′＝45°＝∠EB′D.∴△DEB′是等腰直角三角形．∴DB′DE＝2.∵四边形ABCD是正方形，∴BDCD＝2，∠BDC＝45°.∴BDCD＝DB′DE.∵∠EDB′＝∠BDC，∴∠EDB′＋∠EDB＝∠BDC＋∠EDB，即∠B′DB＝∠EDC.∴△B′DB∽△EDC.∴BB′CE＝BDCD＝2.②BEB′E的值为3或1.∵四边形ABCD是正方形，∴BDCD＝2，∠BDC＝45°.∴BDCD＝DB′DE.∵∠EDB′＝∠BDC，∴∠EDB′＋∠EDB＝∠BDC＋∠EDB，即∠B′DB＝∠EDC.∴△B′DB∽△EDC.∴BB′CE＝BDCD＝2.②BEB′E的值为3或1.训练4.(2020十堰)如图1，已知△ABC≌△EBD，∠ACB＝∠EDB＝90°，点D在AB上，连接CD并延长交AE于点F.(1)猜想：线段AF与EF的数量关系为__________；(2)探究：若将图1的△EBD绕点B顺时针方向旋转，当∠CBE小于180°时，得到图2，连接CD并延长交AE于点F，则(1)中的结论是否还成立？若成立，请证明；若不成立，请说明理由；AF＝EF第4题图1第4题图2解：(2)(1)中的结论还成立．理由如下：如答图10，延长DF到点K，并使FK＝DC，连接KE.设BD延长线DM交AE于点M.∵△ABC≌△EBD，∴ED＝AC，BD＝BC.∴∠CDB＝∠DCB.又∠CDB＝∠MDF，∴∠MDF＝∠DCB.∵∠ACB＝∠EDB＝90°，∴∠ACD＋∠DCB＝∠MDF＋∠FDE＝90°.∴∠ACD＝∠FDE.答图10∵FK＋DF＝DC＋DF，∴DK＝CF.在△ACF和△EDK中，AC＝ED，∠ACF＝∠EDK，CF＝DK，∴△ACF≌△EDK(SAS)．∴EK＝AF，∠K＝∠AFC.又∠AFC＝∠KFE，∴∠K＝∠KFE.∴EK＝EF.∴AF＝EF.∵FK＋DF＝DC＋DF，∴DK＝CF.在△ACF和△EDK中，AC＝ED，∠ACF＝∠EDK，CF＝DK，∴△ACF≌△EDK(SAS)．∴EK＝AF，∠K＝∠AFC.又∠AFC＝∠KFE，∴∠K＝∠KFE.∴EK＝EF.∴AF＝EF.(3)拓展：图1中，过点E作EG⊥CB，垂足为点G.当∠ABC的大小发生变化，其他条件不变时，若∠EBG＝∠BAE，BC＝6，直接写出AB的长．解：AB＝12.第4题图15．如图1，在矩形ABCD中，AB＝2，BC＝5，BP＝1，∠MPN＝90°，将∠MPN绕点P从PB处开始按顺时针方向旋转，PM交边AB(或AD)于点E，PN交边AD(或CD)于点F.当PN旋转至PC处时，∠MPN的旋转随即停止．(1)特殊情形：如图2，发现当PM过点A时，PN也恰好过点D，此时△ABP是否与△PCD相似？并说明理由．图1图2解：(1)△ABP∽△PCD.理由如下：∵四边形ABCD为矩形，∴∠B＝∠C＝90°.∴∠BAP＋∠BPA＝90°.∵∠MPN＝90°，∴∠BPA＋∠CPD＝90°.∴∠BAP＝∠CPD.∴△ABP∽△PCD.(2)类比探究：如图3，在旋转过程中，PEPF的值是否为定值？若是，请求出该定值；若不是，请说明理由．图3(2)类比探究：如图3，在旋转过程中，PEPF的值是否为定值？若是，请求出该定值；若不是，请说明理由．答图11解：PEPF的值是定值，为12.理由如下：如答图11，过点F作FH⊥PC于点H.在矩形ABCD中，AB＝2，∴∠B＝∠FHP＝90°，HF＝AB＝2.∴∠BPE＋∠BEP＝90°.∵∠MPN＝90°，∴∠BPE＋∠HPE＝90°.∴∠BEP＝∠HPF.∴△BEP∽△HPF.∴PEFP＝BPHF.∵BP＝1，∴PEPF＝12.解：PEPF的值是定值，为12.理由如下：如答图11，过点F作FH⊥PC于点H.在矩形ABCD中，AB＝2，∴∠B＝∠FHP＝90°，HF＝AB＝2.∴∠BPE＋∠BEP＝90°.∵∠MPN＝90°，∴∠BPE＋∠HPE＝90°.∴∠BEP＝∠HPF.∴△BEP∽△HPF.∴PEFP＝BPHF.∵BP＝1，∴PEPF＝12.(3)拓展延伸：设AE＝t时，△EPF的面积为S，试用含t的代数式表示S.①在旋转过程中，若t＝1，求对应的△EPF的面积；②在旋转过程中，当△EPF的面积为4.2时，求对应的t的值．解：分两种情况：如答图11，当点E在AB上时，0≤t≤2.∵AE＝t，AB＝2，∴BE＝2－t.由(2)可知△BEP∽△HPF，∴BEHP＝PEFP，即2－tHP＝12.∴HP＝4－2t.在矩形ABCD中，∠A＝∠B＝90°.解：分两种情况：如答图11，当点E在AB上时，0≤t≤2.∵AE＝t，AB＝2，∴BE＝2－t.由(2)可知△BEP∽△HPF，∴BEHP＝PEFP，即2－tHP＝12.∴HP＝4－2t.在矩形ABCD中，∠A＝∠B＝90°.又∠FHB＝90°，∴四边形ABHF为矩形．∴AF＝BH＝BP＋HD＝5－2t.∴S＝S矩形ABHF－S△AEF－S△BEP－S△PHF＝AB·AF－12AE·AF－12BE·PB－12PH·FH＝t2－4t＋5(0≤t≤2)．①若t＝1，S＝1－4＋5＝2.②当S＝4.2时，t2－4t＋5＝4.2，解得t＝2－455或t＝2＋455(舍去)．又∠FHB＝90°，∴四边形ABHF为矩形．∴AF＝BH＝BP＋HD＝5－2t.∴S＝S矩形ABHF－S△AEF－S△BEP－S△PHF＝AB·AF－12AE·AF－12BE·PB－12PH·FH＝t2－4t＋5(0≤t≤2)．①若t＝1，S＝1－4＋5＝2.②当S＝4.2时，t2－4t＋5＝4.2，解得t＝2－455或t＝2＋455(舍去)．如答图12，当点E在AD上时，0≤t≤1，过点E作EK⊥BP于点K.答图12∵四边形ABCD是矩形，∴AD＝BC＝5，CD＝AB＝2.∵AE＝t，∴PK＝1－t，ED＝5－t.同理可证△PKE∽△FCP，四边形EKCD为矩形．∴EK＝CD＝2，KC＝ED＝5－t.∴CP＝KC－PK＝4.∵四边形ABCD是矩形，∴AD＝BC＝5，CD＝AB＝2.∵AE＝t，∴PK＝1－t，ED＝5－t.同理可证△PKE∽△FCP，四边形EKCD为矩形．∴EK＝CD＝2，KC＝ED＝5－t.∴CP＝KC－PK＝4.∴PKFC＝EKCP，即1－tFC＝24.∴FC＝2－2t.∴DF＝CD－FC＝2t.∴S＝S矩形EKCD－S△EKP－S△EDF－S△PCF＝CD·DE－12EK·PK－12ED·DF－12CP·FC＝t2－2t＋5(0≤t≤1)．①若t＝1，S＝1－2＋5＝4.②当S＝4.2时，t2－2t＋5＝4.2，∴PKFC＝EKCP，即1－tFC＝24.∴FC＝2－2t.∴DF＝CD－FC＝2t.∴S＝S矩形EKCD－S△EKP－S△EDF－S△PCF＝CD·DE－12EK·PK－12ED·DF－12CP·FC＝t2－2t＋5(0≤t≤1)．①若t＝1，S＝1－2＋5＝4.②当S＝4.2时，t2－2t＋5＝4.2，解得t＝1－55或t＝1＋55(舍去)．综上所述，当点E在AB上时，S＝t2－4t＋5(0≤t≤2)，若t＝1，S＝2，当S＝4.2时，t＝2－455；当点E在AD上时，S＝t2－2t＋5(0≤t≤1)，若t＝1，S＝4，当S＝4.2时，t＝1－55.解得t＝1－55或t＝1＋55(舍去)．综上所述，当点E在AB上时，S＝t2－4t＋5(0≤t≤2)，若t＝1，S＝2，当S＝4.2时，t＝2－455；当点E在AD上时，S＝t2－2t＋5(0≤t≤1)，若t＝1，S＝4，当S＝4.2时，t＝1－55.6．【发现证明】(1)如图1，在正方形ABCD中，点E，F分别是BC，CD边上的动点，且∠EAF＝45°，求证：EF＝DF＋BE.小明发现，当把△ABE绕点A顺时针旋转90°至△ADG，使AB与AD重合时能够证明，请你给出证明过程．图1(1)证明：由旋转的性质可知∠BAE＝∠DAG，AE＝AG，BE＝DG.在正方形ABCD中，∠BAD＝90°，∠EAF＝45°，∴∠BAE＋∠FAD＝45°.∴∠DAG＋∠FAD＝45°.∴∠EAF＝∠GAF.∵AF＝AF，∴△EAF≌△GAF(SAS)．∴EF＝GF＝DF＋DG.∴EF＝DF＋BE.【类比引申】(2)①如图2，在正方形ABCD中，如果点E，F分别是CB，DC延长线上的动点，且∠EAF＝45°，则(1)中的结论还成立吗？若成立，请写出证明过程；若不成立，请写出正确的结论并说明理由．②如图3，如果点E，F分别是BC，CD延长线上的动点，且∠EAF＝45°，则EF，BE，DF之间的数量关系是______________.BE＝EF＋DF图2图3解：①不成立，正确的结论：EF＝DF－BE.理由：如答图13，将△ABE绕点A顺时针旋转90°至△ADM，则∠EAB＝∠MAD，AE＝AM，∠EAM＝90°，BE＝DM.∵∠BAD＝∠BAM＋∠MAD＝90°，∴∠BAM＋∠EAB＝∠EAM＝90°.∴∠MAF＝45°＝∠EAF.∵AF＝AF，∴△EAF≌△MAF(SAS)．答图13【联想拓展】(3)如图1，若正方形ABCD的边长为6，AE＝35，求AF的长．解：由(1)可知AG＝AE＝35.∵正方形ABCD的边长为6，∴DC＝BC＝AD＝6.∴DG＝AG2－AD2＝352－62＝3.∴BE＝DG＝3.∴CE＝BC－BE＝6－3＝3.【联想拓展】(3)如图1，若正方形ABCD的边长为6，AE＝35，求AF的长．解：由(1)可知AG＝AE＝35.∵正方形ABCD的边长为6，∴DC＝BC＝AD＝6.∴DG＝AG2－AD2＝352－62＝3.∴BE＝DG＝3.∴CE＝BC－BE＝6－3＝3.设DF＝x，则EF＝FG＝x＋3，CF＝6－x.在Rt△EFC中，CF2＋CE2＝EF2，∴(6－x)2＋32＝(x＋3)2.解得x＝2.∴DF＝2.∴AF＝AD2＋DF2＝62＋22＝210.∴AF的长为210.设DF＝x，则EF＝FG＝x＋3，CF＝6－x.在Rt△EFC中，CF2＋CE2＝EF2，∴(6－x)2＋32＝(x＋3)2.解得x＝2.∴DF＝2.∴AF＝AD2＋DF2＝62＋22＝210.∴AF的长为210.②命题：如图1，在四边形ABCD中，AB＝AD，CB＝CD，则四边形ABCD是神奇四边形．此命题是______(填“真”或“假”)命题；③神奇四边形的中点四边形是________；例3定义：我们把对角线互相垂直的四边形叫做神奇四边形．顺次连接四边形各边中点得到的四边形叫做中点四边形．(1)判断：①在平行四边形、矩形、菱形中，一定是神奇四边形的是________；新定义探究类型3菱形真矩形图1(2)如图2，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接BE，CG，GE.①求证：四边形BCGE是神奇四边形；②若AC＝2，AB＝5，求GE的长；图2(2)如图2，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接BE，CG，GE.①求证：四边形BCGE是神奇四边形；②若AC＝2，AB＝5，求GE的长；(2)①证明：如答图14，连接CE，BG交于点N，CE交AB于点M.∵四边形ACFG、四边形ABDE是正方形，∴AB＝AE，AG＝AC，∠CAG＝∠BAE＝90°.∴∠GAB＝∠CAE＝90°＋∠CAB.∴△GAB≌△CAE(SAS)．∴∠AEC＝∠ABG.∵∠AEC＋∠AME＝90°，∠BMN＝∠AME，答图14②解：∵AC＝2，AB＝5，∴BC＝AB2－AC2＝5－4＝1.∵四边形ACFG、四边形ABDE是正方形，AC＝2，AB＝5，∴CG＝2AC＝22，BE＝2AB＝10.∵CG2＝CN2＋GN2，BE2＝BN2＋NE2，BC2＝CN2＋BN2，GE2＝GN2＋NE2，∴CG2＋BE2＝BC2＋GE2.∴GE＝8＋10－1＝17.②解：∵AC＝2，AB＝5，∴BC＝AB2－AC2＝5－4＝1.∵四边形ACFG、四边形ABDE是正方形，AC＝2，AB＝5，∴CG＝2AC＝22，BE＝2AB＝10.∵CG2＝CN2＋GN2，BE2＝BN2＋NE2，BC2＝CN2＋BN2，GE2＝GN2＋NE2，∴CG2＋BE2＝BC2＋GE2.∴GE＝8＋10－1＝17.(3)如图3，四边形ABCD是神奇四边形，若AB＝6，CD＝5，AD，BC分别是方程x2－(k＋4)x＋4k＝0的两根，求k的值．图3(3)如图3，四边形ABCD是神奇四边形，若AB＝6，CD＝5，AD，BC分别是方程x2－(k＋4)x＋4k＝0的两根，求k的值．(3)解：∵四边形ABCD是神奇四边形，∴同(2)中②的证明方法，可得AD2＋BC2＝AB2＋CD2.∵AB＝6，CD＝5，∴AD2＋BC2＝41.∵AD，BC分别是方程x2－(k＋4)x＋4k＝0的两根，∴AD＋BC＝k＋4，AD·BC＝4k.∵AD2＋BC2＝41＝(AD＋BC)2－2AD·BC，∴(k＋4)2－8k＝41.∴k1＝5，k2＝－5(不合题意，舍去)．∴k＝5.(3)解：∵四边形ABCD是神奇四边形，∴同(2)中②的证明方法，可得AD2＋BC2＝AB2＋CD2.∵AB＝6，CD＝5，∴AD2＋BC2＝41.∵AD，BC分别是方程x2－(k＋4)x＋4k＝0的两根，∴AD＋BC＝k＋4，AD·BC＝4k.∵AD2＋BC2＝41＝(AD＋BC)2－2AD·BC，∴(k＋4)2－8k＝41.∴k1＝5，k2＝－5(不合题意，舍去)．∴k＝5.训练7.【阅读理解】如图1，在正多边形A1A2A3…An的边A2A3上任取一不与点A2重合的点B2，并以线段A1B2为边在线段A1A2的上方作正多边形A1B2B3…Bn，把正多边形A1B2B3…Bn叫正多边形A1A2…An的准位似图形，点A3称为准位似中心．【特例论证】(1)如图2，已知正三角形A1A2A3的准位似图形为正三角形A1B2B3，试证明：随着点B2的运动，∠B3A3A1的大小始终不图1图2(1)证明：∵△A1A2A3与△A1B2B3是正三角形，∴A1A2＝A1A3，A1B2＝A1B3，∠A2A1A3＝∠B2A1B3＝∠A2＝60°.∴∠A2A1B2＝∠A3A1B3＝60°－∠B2A1A3.∴△A2A1B2≌△A3A1B3(SAS)．∴∠B3A3A1＝∠A2＝60°.∴∠B3A3A1的大小始终不变．【数学思考】(2)如图3，已知正方形A1A2A3A4的准位似图形为正方形A1B2B3B4，随着点B2的运动，∠B3A3A4的大小是否始终不变？若不变，请求出∠B3A3A4的大小；若改变，请说明理由．图3解：∠B3A3A4的大小始终不变．如答图15，在边A1A2上取一点D，使A1D＝A3B2，连接B2D.∵四边形A1A2A3A4与四边形A1B2B3B4是正方形，∴A1A2＝A2A3，A1B2＝B2B3，∠A1B2B3＝∠A1A2A3＝∠A4A3A2＝90°.答图15∴∠A3B2B3＋∠A1B2A2＝90°，∠DA1B2＋∠A1B2A2＝90°.∴∠A3B2B3＝∠DA1B2.∴△A3B2B3≌△DA1B2(SAS)．∴∠B2A3B3＝∠A1DB2.∵A1A2＝A2A3，A1D＝A3B2，∴A2D＝A2B2.∵∠A1A2A3＝90°，∴△DA2B2是等腰直角三角形．∴∠A2DB2＝45°.【归纳猜想】(3)在图1的情况下：①试猜想∠B3A3A4的大小是否会发生改变？若不改变，请用含n的代数式表示出∠B3A3A4的大小(直接写出结果)；若改变，请说明理由．②∠B3A3A4＋∠B4A4A5＋∠B5A5A6＋…＋∠BnAnA1＝_______________.(用含n的代数式表示)解：①∠B3A3B4的大小始终不变，∠B3A3A4＝180°n.90°n－1n－2n解：①∠B3A3B4的大小始终不变，∠B3A3A4＝180°n.90°n－1n－2n8．(2020南通)【了解概念】有一组对角互余的凸四边形称为对余四边形，连接这两个角的顶点的线段称为对余线．【理解运用】(1)如图1，对余四边形ABCD中，AB＝5，BC＝6，CD＝4，连接AC.若AC＝AB，求sin∠CAD的值；(2)如图2，凸四边形ABCD中，AD＝图1图2解：(1)如答图16，过点A作AE⊥BC于点E，过点C作CF⊥AD于点F，则∠AEB＝∠CFD＝90°.答图16∵AC＝AB，BC＝6，∴BE＝CE＝3.在Rt△AEB中，AE＝AB2－BE2＝52－32＝4，∵CF⊥AD，∴∠D＋∠FCD＝90°.∵四边形ABCD是对余四边形，∴∠B＋∠D＝90°.∴∠B＝∠FCD.∵AC＝AB，BC＝6，∴BE＝CE＝3.在Rt△AEB中，AE＝AB2－BE2＝52－32＝4，∵CF⊥AD，∴∠D＋∠FCD＝90°.∵四边形ABCD是对余四边形，∴∠B＋∠D＝90°.∴∠B＝∠FCD.∵∠AEB＝∠DFC＝90°，∴△AEB∽△DFC.∴EBFC＝ABDC.∴3FC＝54.∴FC＝125.∴sin∠CAD＝FCAC＝1255＝1225.∵∠AEB＝∠DFC＝90°，∴△AEB∽△DFC.∴EBFC＝ABDC.∴3FC＝54.∴FC＝125.∴sin∠CAD＝FCAC＝1255＝1225.(2)结论：四边形ABCD是对余四边形．证明：如答图17，过点D作DM⊥DC，使得DM＝DC，连接CM，BM，则△CDM是等腰直角三角形．∴∠DCM＝∠DMC＝45°，∠CDM＝90°.在四边形ABCD中，AD＝BD，AD⊥BD，∴∠DAB＝∠DBA＝45°，∠ADB＝90°＝∠CDM.∴∠ADC＝∠BDM＝90°＋∠BDC.答图17∵AD＝BD，DC＝DM，∴△ADC≌△BDM(SAS)．∴AC＝BM.∵2CD2＋CB2＝AC2，CM2＝DM2＋CD2＝2CD2，∴CM2＋CB2＝BM2.∴∠BCM＝90°.∴∠DCB＝90°－∠DCM＝45°.∴∠DAB＋∠DCB＝90°.∴四边形ABCD是对余四边形．【拓展提升】(3)在平面直角坐标系中，点A(－1,0)，B(3,0)，C(1,2)，四边形ABCD是对余四边形，点E在对余线BD上，且位于△ABC内部，∠AEC＝90°＋∠ABC.设AEBE＝u，点D的纵坐标为t，请直接写出u关于t的函数解析式．解：u关于t的函数解析式为u＝t2(0＜t＜4)．【拓展提升】(3)在平面直角坐标系中，点A(－1,0)，B(3,0)，C(1,2)，四边形ABCD是对余四边形，点E在对余线BD上，且位于△ABC内部，∠AEC＝90°＋∠ABC.设AEBE＝u，点D的纵坐标为t，请直接写出u关于t的函数解析式．解：u关于t的函数解析式为u＝t2(0＜t＜4)．9．定义：有一组对角互补的四边形叫做互补四边形．(1)概念理解①在互补四边形ABCD中，∠A与∠C是一组对角，若∠B∶∠C∶∠D＝2∶3∶4，则∠A＝______°；②如图1，在△ABC中，点D，E分别在边AB，BC上，且BE·BC＝AB·BD，求证：四边形ADEC是互补四边形．90图1(1)②证明：∵BE·BC＝AB·BD，∴BEBA＝BDBC.又∠B＝∠B，∴△BDE∽△BCA.∴∠BED＝∠A.∴∠A＋∠CED＝∠BED＋∠CED＝180°.∴四边形ADEC是互补四边形．(1)②证明：∵BE·BC＝AB·BD，∴BEBA＝BDBC.又∠B＝∠B，∴△BDE∽△BCA.∴∠BED＝∠A.∴∠A＋∠CED＝∠BED＋∠CED＝180°.∴四边形ADEC是互补四边形．(2)探究发现如图2，在等腰三角形ABE中，AE＝BE，点C，D分别在边BE，AE上，AD＝BC，四边形CEDH是互补四边形，求证：∠ABD＝∠BAC＝12∠E.图2(2)探究发现如图2，在等腰三角形ABE中，AE＝BE，点C，D分别在边BE，AE上，AD＝BC，四边形CEDH是互补四边形，求证：∠ABD＝∠BAC＝12∠E.(2)证明：∵AE＝BE，AD＝BC，∴ED＝EC.在△EAC和△EBD中，AE＝BE，∠E＝∠E，EC＝ED，∴△EAC≌△EBD(SAS)．∴∠EAC＝∠EBD.∵AE＝BE，∴∠EAB＝∠EBA.∴∠BAC＝∠ABD.∵四边形CEDH是互补四边形，∴∠E＋∠DHC＝180°.∵∠AHB＝∠DHC，∴∠E＋∠AHB＝180°.∴∠ABD＋∠BAC＝∠E.∴∠ABD＝∠BAC＝12∠E.(2)证明：∵AE＝BE，AD＝BC，∴ED＝EC.在△EAC和△EBD中，AE＝BE，∠E＝∠E，EC＝ED，∴△EAC≌△EBD(SAS)．∴∠EAC＝∠EBD.∵AE＝BE，∴∠EAB＝∠EBA.∴∠BAC＝∠ABD.∵四边形CEDH是互补四边形，∴∠E＋∠DHC＝180°.∵∠AHB＝∠DHC，∴∠E＋∠AHB＝180°.∴∠ABD＋∠BAC＝∠E.∴∠ABD＝∠BAC＝12∠E.(3)推广运用如图3，在△ABE中，点C，D分别在边BE，AE上，AD＝BC，四边形CEDH是互补四边形，若∠E＝60°，AB＝6，AE＝203，求DHCE的值．图3(3)推广运用如图3，在△ABE中，点C，D分别在边BE，AE上，AD＝BC，四边形CEDH是互补四边形，若∠E＝60°，AB＝6，AE＝203，求DHCE的值．(3)解：如答图18，作BF⊥HC于点F，AG⊥HD交HD的延长线于点G，则∠AGD＝∠BFC＝90°.答图18∵四边形CEDH是互补四边形，∴∠EDH＋∠ECH＝180°.∵∠ECH＋∠BCF＝180°，∴∠BCF＝∠EDH＝∠ADG.在△ADG和△BCF中，∠AGD＝∠BFC，∠ADG＝∠BCF，AD＝BC，∴△ADG≌△BCF(AAS)．∴AG＝BF.∵四边形CEDH是互补四边形，∴∠EDH＋∠ECH＝180°.∵∠ECH＋∠BCF＝180°，∴∠BCF＝∠EDH＝∠ADG.在△ADG和△BCF中，∠AGD＝∠BFC，∠ADG＝∠BCF，AD＝BC，∴△ADG≌△BCF(AAS)．∴AG＝BF.在△ABG和△BAF中，AB＝BA，AG＝BF，∴Rt△ABG≌Rt△BAF(HL)．由(2)得∠HAB＋∠HBA＝∠E＝60°，∴∠HAB＝∠HBA＝12∠E＝30°.在Rt△AGH中，∠AHG＝∠HAB＋∠HBA＝60°，∴∠GAH＝30°.设GH＝x，则AG＝3x，AH＝2x，∴AB＝2AG＝23x＝6.∴x＝3.∴AH＝23.∵∠DAH＝∠CAE，∠DHA＝∠E＝60°，∴△ADH∽△ACE.∴DHCE＝AHAE＝23203＝3310.在△ABG和△BAF中，AB＝BA，AG＝BF，∴Rt△ABG≌Rt△BAF(HL)．由(2)得∠HAB＋∠HBA＝∠E＝60°，∴∠HAB＝∠HBA＝12∠E＝30°.在Rt△AGH中，∠AHG＝∠HAB＋∠HBA＝60°，∴∠GAH＝30°.设GH＝x，则AG＝3x，AH＝2x，∴AB＝2AG＝23x＝6.∴x＝3.∴AH＝23.∵∠DAH＝∠CAE，∠DHA＝∠E＝60°，∴△ADH∽△ACE.∴DHCE＝AHAE＝23203＝3310.例4【问题情境】(1)我们曾经研究过这样的问题：已知正方形ABCD，点E在CD的延长线上，以CE为一边构造正方形CEFG，连接BE和DG，如图1所示，则DG和BE的数量关系为__________，位置关系为__________.操作探究类型4DG＝BEDG⊥BE图1【继续探究】(2)若正方形ABCD的边长为4，点E是AD边上的一个动点，以CE为一边在CE的右侧作正方形CEFG，连接DG，BE，如图2所示，①请判断线段DG与BE有怎样的数量关系和位置关系，并说明理由；②连接BG，若AE＝1，求线段BG的长．爱动脑筋的小丽同学是这样做的：过点G作GH⊥BC，如图3，你能按照她的思路做下去图2图3解：(2)①结论：DG＝BE，DG⊥BE.理由：如答图19，延长BE，GD交于点H.∵四边形ABCD、四边形CEFG是正方形，∴BC＝DC，∠BCD＝∠ECG＝90°，CE＝CG.∴∠BCE＝∠DCG＝90°－∠ECD.∴△BCE≌△DCG(SAS)．∴∠EBC＝∠GDC，BE＝DG.∵∠CDG＋∠CDH＝180°，∴∠EBC＋∠CDH＝180°.∵∠EBC＋∠BCD＋∠CDH＋∠DHE＝360°，答图19②∵正方形ABCD的边长为4，∴AD＝DC＝BC＝4.∵AE＝1，AD＝4，∴DE＝3.∵∠ECG＝∠DCH＝90°，∴∠ECD＝∠GCH.又EC＝GC，∠EDC＝∠H＝90°，∴△ECD≌△GCH(AAS)．∴HG＝DE＝3，CH＝CD＝4.∴BH＝BC＋CN＝8.∴BG＝BH2＋HG2＝82＋32＝73.②∵正方形ABCD的边长为4，∴AD＝DC＝BC＝4.∵AE＝1，AD＝4，∴DE＝3.∵∠ECG＝∠DCH＝90°，∴∠ECD＝∠GCH.又EC＝GC，∠EDC＝∠H＝90°，∴△ECD≌△GCH(AAS)．∴HG＝DE＝3，CH＝CD＝4.∴BH＝BC＋CN＝8.∴BG＝BH2＋HG2＝82＋32＝73.【拓展提升】(3)在(2)的条件下，点E在AD边上运动时，利用图2，求BG＋BE的最小值．图2解：由(2)可知BE＝DG，CH＝4.如答图20，点G的运动轨迹是直线GH，直线GH与直线CD之间的距离为4.作点D关于直线GH的对称点T，连接BT，GT.在Rt△ABT中，∠A＝90°，AB＝4，AT＝12，∴BT＝AB2＋AT2＝42＋122＝410.∵BE＝DG，DG＝GT，∴BE＋BG＝BG＋GT.∵GB＋GT≥BT，∴BE＋BG≥410.∴BE＋BG的最小值为410.答图20解：由(2)可知BE＝DG，CH＝4.如答图20，点G的运动轨迹是直线GH，直线GH与直线CD之间的距离为4.作点D关于直线GH的对称点T，连接BT，GT.在Rt△ABT中，∠A＝90°，AB＝4，AT＝12，∴BT＝AB2＋AT2＝42＋122＝410.∵BE＝DG，DG＝GT，∴BE＋BG＝BG＋GT.∵GB＋GT≥BT，∴BE＋BG≥410.∴BE＋BG的最小值为410.训练10.综合与实践【问题情境】在综合与实践课上，老师让同学们以“等腰三角形的剪拼”为主题开展数学活动．如图1，在△ABC中，AB＝AC＝10cm，BC＝16cm.将△ABC沿BC边上的中线AD剪开，得到△ABD和△ACD.【操作发现】(1)乐学小组将图1中的△ACD以点D为旋转中心，按逆时针方向旋转，使得A′C′⊥AD，得到图2，A′C′与AB交于点E，则四边形菱形图1图2(2)缜密小组将图1中的△ACD沿DB方向平移，A′D′与AB交于点M，A′C′与AD交于点N，连接MN，得到图3，判断四边形MNDD′的形状，并说明理由．图3解：(2)四边形MNDD′是矩形．理由如下：∵AB＝AC，AD是BC边上的中线，∴∠B＝∠C，BD＝CD，∠ADB＝∠ADC＝90°.∴BD′＝C′D，∠B＝∠C′，∠MD′B＝∠NDC′.∴△MD′B≌△NDC′(ASA)．∴MD′＝ND.∵△ACD沿DB方向平移，∴MD′∥DN.∴四边形MNDD′是平行四边形．∵∠DD′M＝90°，∴四边形MNDD′是矩形．图1【实践探究】(3)缜密小组又发现，当图3中的线段DD′的长为acm时，四边形MNDD′会成为正方形，求a的值．图3解：∵AB＝10，BD＝8，∴AD＝AB2－BD2＝100－64＝6.∵四边形MNDD′为正方形，∴D′M∥DN，D′M＝D′D＝a.∴△BD′M∽△BDA.∴BD′BD＝MD′AD.∴8－a8＝a6.∴a＝247.解：∵AB＝10，BD＝8，∴AD＝AB2－BD2＝100－64＝6.∵四边形MNDD′为正方形，∴D′M∥DN，D′M＝D′D＝a.∴△BD′M∽△BDA.∴BD′BD＝MD′AD.∴8－a8＝a6.∴a＝247.(4)创新小组又把图1中的△ACD放到如图4所示的位置，点A的对应点A′与点D重合，点D的对应点D′在BD的延长线上，再将△A′C′D′绕点D逆时针旋转到如图5所示的位置，DD′交AB于点P，DC′交AB于点Q，DP＝DQ，此时线段AP的长是______cm.图4图5第10题图656511．综合与探究【问题情境】在综合与实践课上，老师让同学们利用含30°角的直角三角板和一张正方形纸片进行探究活动．如图1，把正方形ABCD的顶点A放在Rt△EFG斜边EG的中点处，正方形的边AB经过直角顶点F，正方形的边AD与直角边FG交于点Q.【探究发现】(1)创新小组发现线段EF，GQ及FQ之间的数量关系为EF2＋GQ2＝FQ2.请加以证明；图1(1)证明：∵AF是Rt△EFG斜边的中线，∴AF＝AE＝AG.∴∠QFA＝∠G＝30°.∵∠E＝90°－∠G＝60°，∴△AFE为等边三角形．∴EF＝AF，∠FAE＝60°.∴∠GAQ＝180°－∠DAB－∠FAE＝30°＝∠G.∴QA＝QG.在Rt△AQF中，FQ2＝AF2＋AQ2＝EF2＋GQ2.【引申探究】(2)如图2，勤奋小组把正方形ABCD绕点A逆时针旋转，边AB与边EF交于点P且不与点E，F重合，把直角三角形的两直角边分成四条线段EP，PF，FQ，GQ，发现这四条线段之间的数量关系是EP2＋GQ2＝FQ2＋FP2，请加以证明；图2(2)证明：如答图21，延长QA到点H使AH＝AQ，连接EH，PQ，PH，∵点A是GE的中点，∴AG＝AE.又AQ＝AH，∠GAQ＝∠EAH，∴△GAQ≌△EAH(SAS)．∴GQ＝EH，∠AEH＝∠G.又∠G＋∠GEF＝90°，答图21∵∠DAB＝90°，AQ＝AH，∴PA是QH的中垂线．∴PH＝PQ.在Rt△PHE中，PH2＝PE2＋HE2＝PE2＋GQ2，在Rt△PQF中，PQ2＝FQ2＋FP2，∴PE2＋GQ2＝FQ2＋FP2.【探究拓广】(3)奇艺小组的同学受勤奋小组同学的启发继续把正方形ABCD绕着点A逆时针旋转，边BA和DA的延长线与两直角边仍交于P，Q两点，按题意完善图3，并直接写出EP，FP，FQ，GQ之间的数量关系．解：完善后的图形如答图22所示，EP，FP，FQ，GQ之间的数量关系为EP2＋GQ2＝FQ2＋FP2.图3答图2212．(2020齐齐哈尔)综合与实践在线上教学中，教师和学生都学习到了新知识，掌握了许多新技能．例如教材八年级下册的数学活动——折纸，就引起了许多同学的兴趣．在经历图形变换的过程中，进一步发展了同学们的空间观念，积累了数学活动经验．实践发现：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；再一次折叠纸片，使点A落在EF上的点N处，并使折痕经过点B，得到折痕BM，把纸片展平，连接AN，如图1.图1(1)折痕BM______(填“是”或“不是”)线段AN的垂直平分线；请判断图中△ABN是什么特殊三角形？答：______________；进一步计算出∠MNE＝______°.(2)继续折叠纸片，使点A落在BC边上的点H处，并使折痕经过点B，得到折痕BG，把纸片展平，如图2，则∠GBN＝______°.是等边三角形6015图2拓展延伸：(3)如图3，折叠矩形纸片ABCD，使点A落在BC边上的点A′处，并且折痕交BC边于点T，交AD边于点S，把纸片展平，连接AA′交ST于点O，连接AT.求证：四边形SATA′是菱形．图3(3)证明：∵折叠矩形纸片ABCD，使点A落在BC边上的点A′处，∴ST垂直平分AA′，∴AO＝A′O，AA′⊥ST，∵四边形ABCD是矩形，∴AD∥BC，∴∠SAO＝∠TA′O，∠ASO＝∠A′TO，∴△ASO≌△A′TO(AAS)．∴SO＝TO.∴四边形SATA′是平行四边形．又AA′⊥ST，∴四边形SATA′是菱形．解决问题：(4)如图4，矩形纸片ABCD中，AB＝10，AD＝26，折叠纸片，使点A落在BC边上的点A′处，并且折痕交AB边于点T，交AD边于点S，把纸片展平．同学们小组讨论后，得出线段AT的长度有4,5,7,9.请写出以上4个数值中你认为正确的数值________.7,9图4例5(2020深圳改编)背景：一次小组合作探究课上，小明将两个正方形按如图1所示的位置摆放(点E，A，D在同一条直线上)，发现BE＝DG且BE⊥DG.小组讨论后，提出了下列三个问题，请你帮助解答：(1)将正方形AEFG绕点A按逆时针方向旋转(如图2)，还能得到BE＝DG吗？若能，请给出证形状变化探究类型5图1图2解：(1)能得到BE＝DG.证明：∵四边形AEFG为正方形，∴AE＝AG，∠EAG＝90°.又四边形ABCD为正方形，∴AB＝AD，∠BAD＝90°.∴∠EAB＝∠GAD＝90°－∠BAG.∴△AEB≌△AGD(SAS)．∴BE＝DG.(2)把背景中的正方形分别改成菱形AEFG和菱形ABCD，将菱形AEFG绕点A按顺时针方向旋转(如图3)，试问当∠EAG与∠BAD的大小满足怎样的关系时，背景中的结论BE＝DG仍成立？请说明理由；图3解：当∠EAG＝∠BAD时，BE＝DG，理由如下：∵∠EAG＝∠BAD，∴∠EAB＝∠GAD.又四边形AEFG和四边形ABCD为菱形，∴AE＝AG，AB＝AD.∴△AEB≌△AGD(SAS)．∴BE＝DG.(3)把背景中的正方形分别改写成矩形AEFG和矩形ABCD，且AEAG＝ABAD＝23，AE＝4，AB＝8，将矩形AEFG绕点A按顺时针方向旋转(如图4)，连接DE，BG.小组发现：在旋转过程中，DE2＋BG2的值是定值，请求出这个定值．图4(3)把背景中的正方形分别改写成矩形AEFG和矩形ABCD，且AEAG＝ABAD＝23，AE＝4，AB＝8，将矩形AEFG绕点A按顺时针方向旋转(如图4)，连接DE，BG.小组发现：在旋转过程中，DE2＋BG2的值是定值，请求出这个定值．解：方法一：如答图23，过点E作EM⊥DA，交DA的延长线于点M，过点G作GN⊥AB交AB于点N.∵AEAG＝ABAD＝23，AE＝4，AB＝8，∴AG＝6，AD＝12.∵四边形AEFG和四边形ABCD是矩形，∴∠EAG＝∠MAN＝90°.∴∠MAE＝∠GAN＝90°－∠MAG.答图23解：方法一：如答图23，过点E作EM⊥DA，交DA的延长线于点M，过点G作GN⊥AB交AB于点N.∵AEAG＝ABAD＝23，AE＝4，AB＝8，∴AG＝6，AD＝12.∵四边形AEFG和四边形ABCD是矩形，∴∠EAG＝∠MAN＝90°.∴∠MAE＝∠GAN＝90°－∠MAG.∵∠EMA＝∠ANG，∴△AME∽△ANG.∴EMGN＝AMAN＝AEAG＝23.设EM＝2a，AM＝2b，则GN＝3a，AN＝3b.∴BN＝8－3b.∵AE2＝AM2＋EM2＝42，∴(2b)2＋(2a)2＝16.∴a2＋b2＝4.∵ED2＝(2a)2＋(12＋2b)2＝4a2＋144＋48b＋4b2，GB2＝(3a)2＋(8－3b)2＝9a2＋64－48b＋9b2，∴ED2＋GB2＝13(a2＋b2)＋208＝13×4＋208＝260.∵∠EMA＝∠ANG，∴△AME∽△ANG.∴EMGN＝AMAN＝AEAG＝23.设EM＝2a，AM＝2b，则GN＝3a，AN＝3b.∴BN＝8－3b.∵AE2＝AM2＋EM2＝42，∴(2b)2＋(2a)2＝16.∴a2＋b2＝4.∵ED2＝(2a)2＋(12＋2b)2＝4a2＋144＋48b＋4b2，GB2＝(3a)2＋(8－3b)2＝9a2＋64－48b＋9b2，∴ED2＋GB2＝13(a2＋b2)＋208＝13×4＋208＝260.方法二：如答图24，设BE与DG交于点Q，BE与AG交于点P，连接EG，BD.∵AEAG＝ABAD＝23，AE＝4，AB＝8，∴AG＝6，AD＝12.∵四边形AEFG和四边形ABCD为矩形，∴∠EAG＝∠BAD＝90°.∴∠EAB＝∠GAD＝90°＋∠GAB.答图24方法二：如答图24，设BE与DG交于点Q，BE与AG交于点P，连接EG，BD.∵AEAG＝ABAD＝23，AE＝4，AB＝8，∴AG＝6，AD＝12.∵四边形AEFG和四边形ABCD为矩形，∴∠EAG＝∠BAD＝90°.∴∠EAB＝∠GAD＝90°＋∠GAB.∵EAGA＝ABAD，∴△EAB∽△GAD.∴∠BEA＝∠DGA.∴A，E，G，Q四点共圆．∴∠GQP＝∠PAE＝90°.∴GD⊥EB.∴ED2＋GB2＝EQ2＋QD2＋GQ2＋QB2＝EG2＋BD2.∴EG2＋BD2＝42＋62＋82＋122＝260.∵EAGA＝ABAD，∴△EAB∽△GAD.∴∠BEA＝∠DGA.∴A，E，G，Q四点共圆．∴∠GQP＝∠PAE＝90°.∴GD⊥EB.∴ED2＋GB2＝EQ2＋QD2＋GQ2＋QB2＝EG2＋BD2.∴EG2＋BD2＝42＋62＋82＋122＝260.训练13.在△ABC中，AC＝BC，∠ACB＝α，点D为直线BC上一动点，过点D作DF∥AC交直线AB于点F，将AD绕点D顺时针旋转α得到ED，ED交直线AB于点O，连接BE.【问题发现】(1)如图1，α＝90°，点D在边BC上，猜想：①AF与BE的数量关系是__________；②∠ABE＝______度．AF＝BE90图1【拓展探究】(2)如图2,0°＜α＜90°，点D在边BC上，猜想AF与BE的数量关系及∠ABE的度数，并给予证明．图2解：(2)猜想：AF＝BE，∠ABE＝α.证明：∵DF∥AC，∴∠FDB＝∠ACB＝α，∠DFB＝∠CAB.∵AC＝BC，∴∠ABC＝∠CAB.∴∠ABC＝∠DFB.∴DB＝DF.∵∠ADF＝∠ADE－∠FDE，∠EDB＝∠FDB－∠FDE，∠ADE＝∠FDB＝α，∴∠ADF＝∠EDB.∵AD＝ED，DF＝DB，∴△ADF≌△EDB(SAS)．∴AF＝EB，∠AFD＝∠EBD.【解决问题】(3)如图3,90°＜α＜180°，点D在射线BC上，且BD＝3CD，若AB＝8，请直接写出BE的长．解：BE的长为2或4.图314．【问题发现】(1)如图1，△ABC和△CDE均为等边三角形，直线AD和直线BE交于点F.填空：①∠AFB的度数是________；②线段AD，BE之间的数量关系为__________.60°AD＝BE图1【类比探究】(2)如图2，△ABC和△CDE均为等腰直角三角形，∠ABC＝∠DEC＝90°，AB＝BC，DE＝EC，直线AD和直线BE交于点F.请判断∠AFB的度数及线段AD，BE之间的数量关系，并说明理由．图2解：结论：∠AFB＝45°，AD＝2BE.理由：∵∠ABC＝∠DEC＝90°，AB＝BC，DE＝EC，∴∠ACD＝45°＋∠BCD＝∠BCE，ACBC＝DCEC＝2.解：结论：∠AFB＝45°，AD＝2BE.理由：∵∠ABC＝∠DEC＝90°，AB＝BC，DE＝EC，∴∠ACD＝45°＋∠BCD＝∠BCE，ACBC＝DCEC＝2.∴△ACD∽△BCE.∴ADBE＝ACBC＝2，∠CBF＝∠CAF.∴AD＝2BE.∵∠AFB＋∠CBF＝∠ACB＋∠CAF，∴∠AFB＝∠ACB＝45°.∴△ACD∽△BCE.∴ADBE＝ACBC＝2，∠CBF＝∠CAF.∴AD＝2BE.∵∠AFB＋∠CBF＝∠ACB＋∠CAF，∴∠AFB＝∠ACB＝45°.(3)如图3，在△ABC中，∠ACB＝90°，∠CAB＝30°，AB＝5，点D在AB边上，DE⊥AC于点E，AE＝3，将△ADE绕着点A在平面内旋转，求直线DE经过点B时BD的长．图3解：如答图25.在Rt△ABE中，AB＝5，AE＝3，∴BE＝AB2－AE2＝4.在Rt△ADE中，AE＝3，∠DAE＝30°，∴DE＝AE·tan30°＝3×33＝3.答图25解：如答图25.在Rt△ABE中，AB＝5，AE＝3，∴BE＝AB2－AE2＝4.在Rt△ADE中，AE＝3，∠DAE＝30°，∴DE＝AE·tan30°＝3×33＝3.∴BD＝BE－DE＝4－3.如答图26，当点D，E，B在同一直线上时，同法可知BD＝EB＋DE＝4＋3.综上所述，BD＝4＋3或4－3.答图26∴BD＝BE－DE＝4－3.如答图26，当点D，E，B在同一直线上时，同法可知BD＝EB＋DE＝4＋3.综上所述，BD＝4＋3或4－3.15．(2020连云港)(1)如图1，点P为矩形ABCD对角线BD上一点，过点P作EF∥BC，分别交AB，CD于点E，F.若BE＝2，PF＝6，△AEP的面积为S1，△CFP的面积为S2，则S1＋S2＝______；(2)如图2，点P为□ABCD内一点(点P不在BD上)，点E，F，G，H分别为各边的中点．设四边形AEPH的面积为S1，四边形PFCG的面积为S2(其中S2＞S1)，求△PBD12图1图2解：(2)如答图27，连接PA，PC.在△APB中，点E是AB的中点，∴可设S△APE＝S△PBE＝a，同理S△APH＝S△PDH＝b，S△PDG＝S△PGC＝c，S△PFC＝S△PBF＝d.∴S四边形AEPH＋S四边形PFCG＝a＋b＋c＋d，S四边形PEBF＋S四边形PHDG＝a＋b＋c＋d.∴S四边形AEPH＋S四边形PFCG＝S四边形PEBF＋S四边形PHDG＝S1＋S2.∴S△ABD＝12S▱ABCD＝S1＋S2.∴S△PDH＝S△ABD－(S1＋S△PBE＋S△PDH)＝S1＋S2－(S1＋a＋S1－a)＝S2－S1.答图27解：(2)如答图27，连接PA，PC.在△APB中，点E是AB的中点，∴可设S△APE＝S△PBE＝a，同理S△APH＝S△PDH＝b，S△PDG＝S△PGC＝c，S△PFC＝S△PBF＝d.∴S四边形AEPH＋S四边形PFCG＝a＋b＋c＋d，S四边形PEBF＋S四边形PHDG＝a＋b＋c＋d.∴S四边形AEPH＋S四边形PFCG＝S四边形PEBF＋S四边形PHDG＝S1＋S2.∴S△ABD＝12S▱ABCD＝S1＋S2.∴S△PDH＝S△ABD－(S1＋S△PBE＋S△PDH)＝S1＋S2－(S1＋a＋S1－a)＝S2－S1.(3)如图3，点P为□ABCD内一点(点P不在BD上)，过点P作EF∥AD，HG∥AB，与各边分别相交于点E，F，G，H.设四边形AEPH的面积为S1，四边形PGCF的面积为S2(其中S2＞S1)，求△PBD的面积(用含S1，S2的代数式表示)；图3解：由题意易证四边形EBGP、四边形HPFD都是平行四边形，∴S四边形EBGP＝2S△EBP，S四边形HPFD＝2S△HPD.∴S△ABD＝12S▱ABCD＝12(S1＋S2＋2S△EBP＋2S△HPD)＝12(S1＋S2)＋S△EBP＋S△HPD.∴S△PBD＝S△ABD－(S1＋S△EBP＋S△HPD)＝12(S2－S1)．解：由题意易证四边形EBGP、四边形HPFD都是平行四边形，∴S四边形EBGP＝2S△EBP，S四边形HPFD＝2S△HPD.∴S△ABD＝12S▱ABCD＝12(S1＋S2＋2S△EBP＋2S△HPD)＝12(S1＋S2)＋S△EBP＋S△HPD.∴S△PBD＝S△ABD－(S1＋S△EBP＋S△HPD)＝12(S2－S1)．(4)如图4，点A，B，C，D把⊙O四等分．请你在圆内选一点P(点P不在AC，BD上)，设PB，PC，BC︵围成的封闭图形的面积为S1，PA，PD，AD︵围成的封闭图形的面积为S2，△PBD的面积为S3，△PAC的面积为S4，根据你选的点P的位置，直接写出一个含有S1，S2，S3，S4的等式(写出一种情况即可)．图4(4)如图4，点A，B，C，D把⊙O四等分．请你在圆内选一点P(点P不在AC，BD上)，设PB，PC，BC︵围成的封闭图形的面积为S1，PA，PD，AD︵围成的封闭图形的面积为S2，△PBD的面积为S3，△PAC的面积为S4，根据你选的点P的位置，直接写出一个含有S1，S2，S3，S4的等式(写出一种情况即可)．解：如答图28，S2－S1＝S3＋S4.如答图29，S1－S2＝S3＋S4.如答图30和答图31，S1－S2＝S3－S4.(任选一种即可)答图28答图29答图30答图31答图28答图29答图30答图31