解题后怎样反思-——以旋转变换为例-课件 (1)

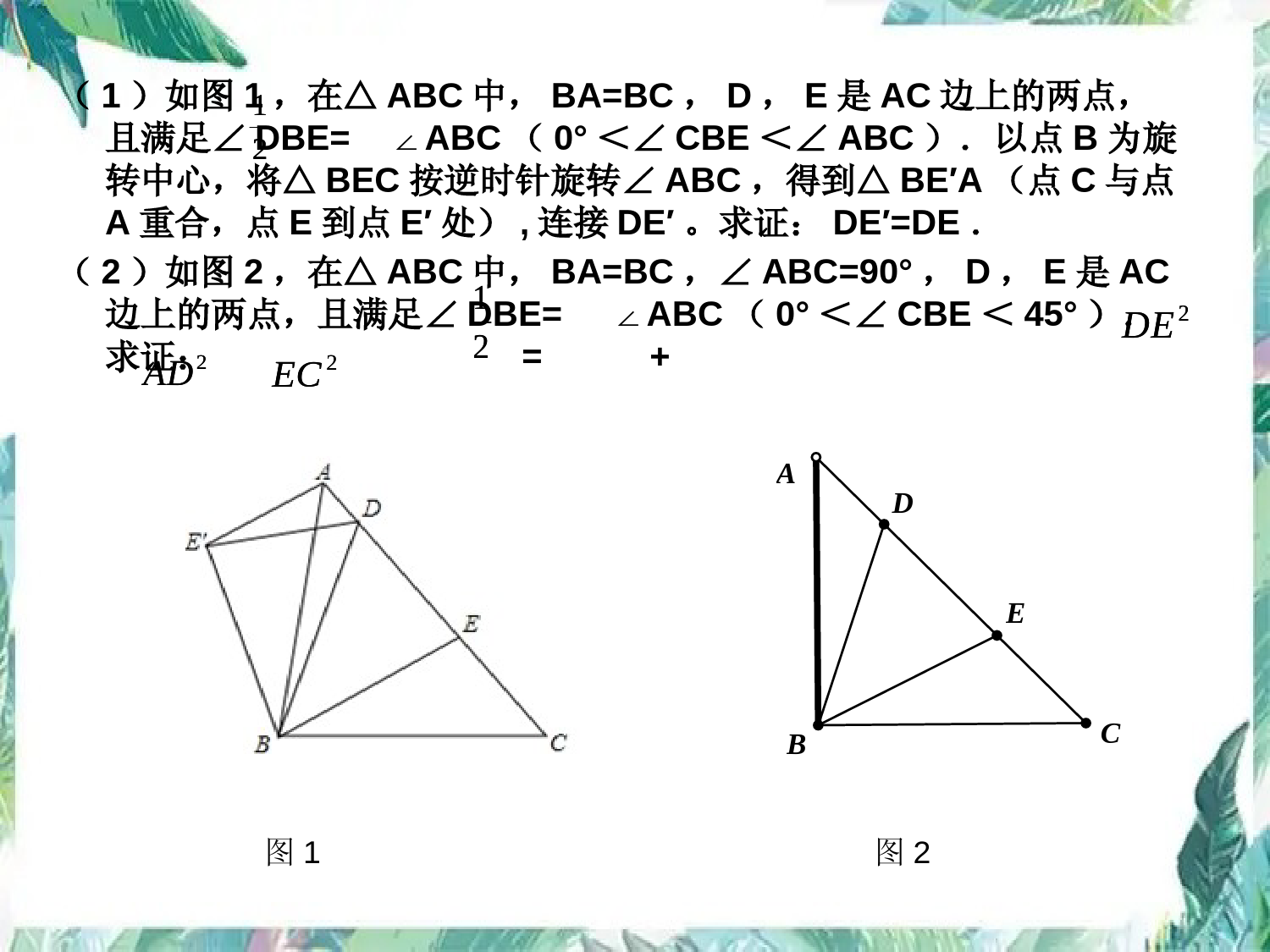
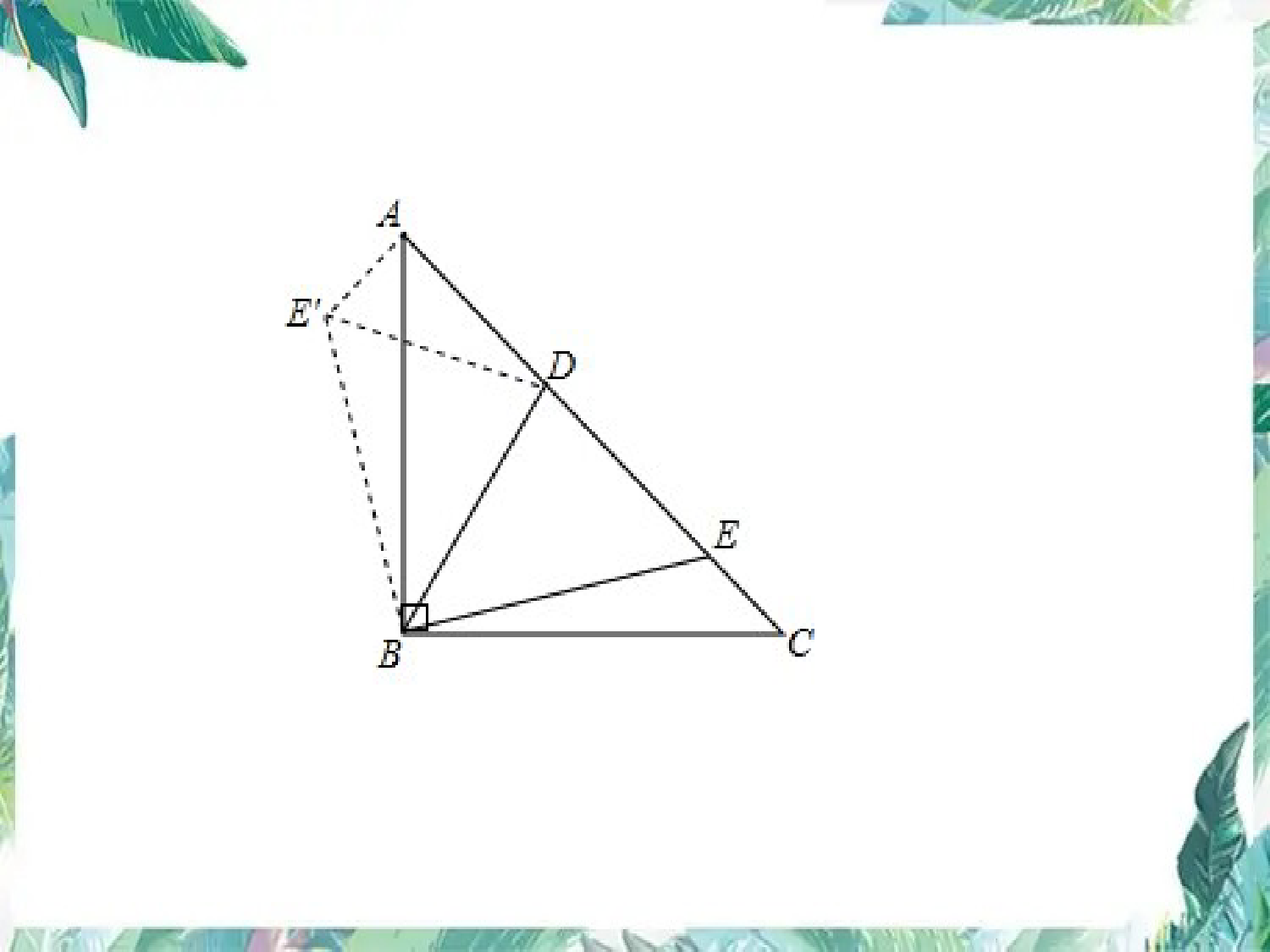
解题后怎样反思(一)——以旋转变换为例国际著名的荷兰数学家弗赖登塔尔指出：“反思是数学思维活动的核心和动力。在数学活动中及时、多角度地反思，能促使从新的角度，多层次、多侧面地对问题进行全面考察、分析与思考，……，对思维能力的提高大有裨益。”（1）如图1，在△ABC中，BA=BC，D，E是AC边上的两点，且满足∠DBE=ABC∠（0°＜∠CBE＜∠ABC）．以点B为旋转中心，将△BEC按逆时针旋转∠ABC，得到△BE′A（点C与点A重合，点E到点E′处）,连接DE′。求证：DE′=DE．（2）如图2，在△ABC中，BA=BC，∠ABC=90°，D，E是AC边上的两点，且满足∠DBE=ABC∠（0°＜∠CBE＜45°）．求证：=+ABCDE图1图221212DE2AD2EC21212DE2AD2EC反思•比较：1、条件：两问中条件有什么共同处？2、解法：两问中解法有什么共同处？反思•拓展1、当∠ABC为锐角时（其它条件不变），AD、DE、EC三边中存在两边的平方和等于另一边的平方吗？反思•拓展BACE'DE反思•拓展3、当∠ABC为钝角时（其它条件不变），BACE'DE反思比较法：条件、解法上共同处拓展法：研究所有情形（1）如图1，在正方形ABCD中，E是AB上一点，G在AD上，且∠GCE＝45°，则GE＝BE＋GD成立吗？为什么？（2）如图2，在直角梯形ABCD中，ADBC∥（BC＞AD），∠B＝90°，AB＝BC＝12，E是AB上一点，且∠DCE＝45°，BE＝4，求DE的长．ADBCEGBCADE图1图2GBACEDADBCEG四边形ABCD中，E是AB上一点，G在AD上，∠GCE=BCD∠。四边形ABCD还需满足什么条件，GE＝BE＋GD仍成立？BCDAEG2121反思比较法：图形上本质联系拓展法：特殊情形到一般情形反思比较法反思：条件、解法、图形上本质的联系拓展法反思：研究所有情形特殊情形到一般情形在△CDE中，∠ECD=45°，CFED⊥于F,EF=2，FD=3。求CF的长。FECDBACGEDF