2023年中考数学复习第一部分考点梳理第七章图形变换第3节图形的平移、对称(折叠)、旋转与位似

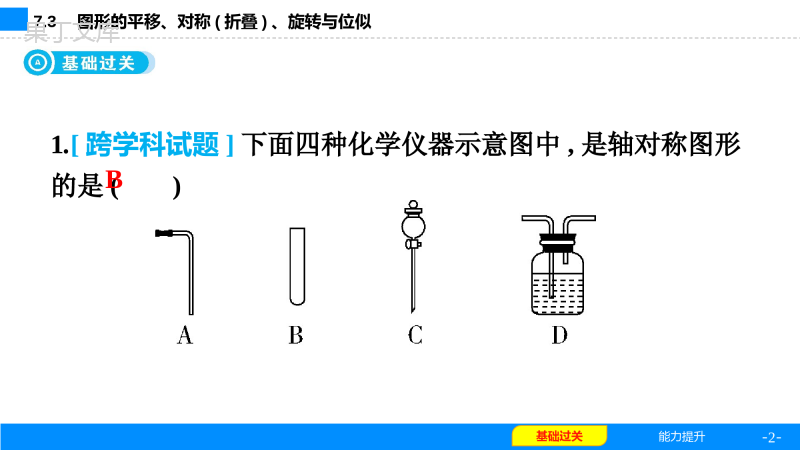
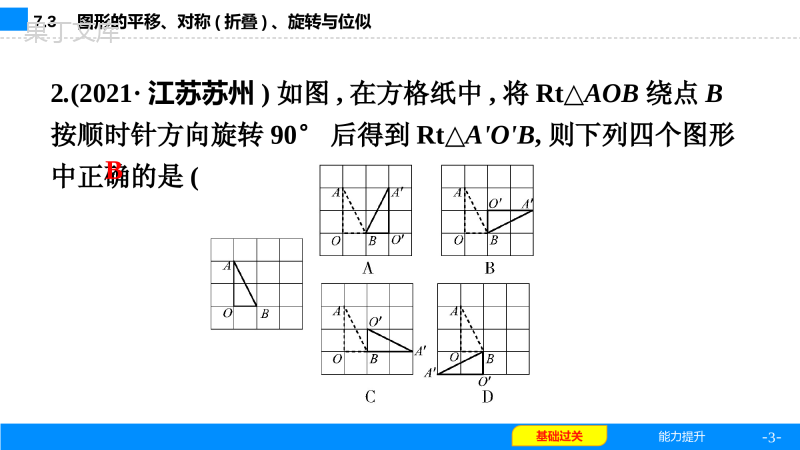
7.3图形的平移、对称(折叠)、旋转与位似-2-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关1.[跨学科试题]下面四种化学仪器示意图中,是轴对称图形的是()B-3-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关2.(2021·江苏苏州)如图,在方格纸中,将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A'O'B,则下列四个图形中正确的是()B-4-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关A.B.1C.2D.3.如图,△OAB的边OB在x轴的正半轴上,O是原点,点B的坐标为(3,0),把△OAB沿x轴向右平移2个单位长度,得到△CDE,连接AC,DB.若△DBE的面积为3,则图中阴影部分的面积为()D-5-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关A.等腰三角形B.直角三角形C.矩形D.菱形4.(2021·浙江嘉兴)将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是()D-6-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关A.1∶2B.1∶4C.1∶3D.1∶95.如图,△ABC与△DEF位似,点O是它们的位似中心,其中OE＝2OB,则△ABC与△DEF的周长之比是()A-7-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关A.108°B.109°C.110°D.111°6.(2022·黑龙江大庆)如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点E处.若∠1＝56°,∠2＝42°,则∠A的度数为()C-8-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关7.[HK版教材九上P110C组复习题第1题改编]如图,在边长为1的正方形网格中,正方形ABCD和正方形OEFG是位似图形,点F的坐标是(1,1),点C的坐标是(4,4),则它们的位似中心的坐标是.(－?,－?)或(??,??)-9-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关【解析】分两种情况讨论:①当位似图形在位似中心同侧时,连接DG,AO交于一点M(－2,－2),该点即为位似中心;②当位似图形在位似中心异侧时,连接DE,AF交于一点N.-10-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关8.正方形网格中的每个小正方形的边长均为1个单位长度,△ABC各顶点的位置如图所示.将△ABC平移,使点A移到点D的位置,E,F分别是B,C的对应点.(1)画出平移后的△DEF;(2)在AB上找一点P,连接CP,使得线段CP平分△ABC的面积.-11-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关解:(1)如图所示,△DEF即为所求.(2)如图所示,线段CP即为所求.-12-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关9.(2022·合肥蜀山区二模)如图,平面直角坐标系中的△ABC的三个顶点坐标分别为A(－5,0),B(－1,－4),C(－1,0),M为线段AB的中点.(1)点M关于y轴的对称点M1的坐标为.(2)画出△ABC关于点O的中心对称图形△A1B1C1(点A,B,C的对应点分别为点A1,B1,C1);(3,－2)-13-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关(3)再将点M1沿y轴正方向平移,在平移过程中,直接写出当平移的距离d在什么范围时,点M1在△A1B1C1的内部(不包括边界).-14-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关解:(2)如图所示,△A1B1C1即为所求.(3)观察图形可知2＜d＜4.-15-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关10.如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A'落在∠ACB的外角平分线CD上,连接AA'.(1)判断四边形ACC'A'的形状,并说明理由;(2)在△ABC中,∠B＝90°,AB＝8,cos∠BAC＝,求CB'的长.-16-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关解:(1)四边形ACC'A'是菱形.理由:由平移的性质可得AA'＝CC',且AA'∥CC',∴四边形ACC'A'是平行四边形,∠AA'C＝∠A'CB'.由题意,得CD平分∠ACB',∴∠ACA'＝∠A'CB',∴∠ACA'＝∠AA'C,∴AA'＝AC,∴四边形ACC'A'是菱形.-17-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升基础过关(2)在Rt△ABC中,∠B＝90°,AB＝8,cos∠BAC＝,∴AC＝10,∴BC＝＝6,∴B'C'＝BC＝6.由(1)得四边形ACC'A'是菱形,∴CC'＝AC＝10,∴CB'＝CC'－B'C'＝10－6＝4.-18-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升能力提升A.(1,－1)B.(0,－)C.(,0)D.(－1,1)11.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2023次得到正方形OA2023B2023C2023.如果点A的坐标为(1,0),那么点B2023的坐标为()C-19-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升能力提升【解析】∵四边形OABC是正方形,且OA＝1,∴点B的坐标为(1,1).连接OB.由勾股定理,得OB＝,由旋转得OB＝OB1＝OB2＝OB3＝…＝.∵每次将正方形绕点O逆时针旋转45°,∴点B1的坐标为(0,),点B2的坐标为(－1,1),点B3的坐标为(－,0),……,且规律是8次一循环.∵2023÷8＝252……7,∴点B2023的坐标为(,0).-20-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升能力提升12.[开放题]如图,在2×6的方格纸中,已知格点P,请按要求画格点图形(顶点均在格点上).(1)在图1中画一个锐角三角形,使P为其中一边的中点,再画出该三角形向右平移2个单位长度后的图形;(2)在图2中画一个以P为一个顶点的钝角三角形,使三边长都不相等,再画出该三角形绕点P旋转180°后的图形.图1图2-21-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升能力提升解:(1)如图1所示,△ABC和△A'B'C'即为所求.(答案不唯一)(2)如图2所示,△DEP和△D'E'P即为所求.(答案不唯一)图1图2-22-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升能力提升13.(2022·四川广元)在Rt△ABC中,AC＝BC,将线段CA绕点C旋转α(0°＜α＜90°),得到线段CD,连接AD,BD.(1)如图1,将线段CA绕点C逆时针旋转α,则∠ADB的度数为.135°-23-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升能力提升(2)将线段CA绕点C顺时针旋转α.①在图2中依题意补全图形,并求∠ADB的度数;②若∠BCD的平分线CE交BD于点F,交DA的延长线于点E,连接BE.用等式表示线段AD,CE,BE之间的数量关系,并证明.图1图2-24-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升能力提升解:(2)①依题意补全图形如图1.由旋转的性质知CD＝CA＝CB,∠ACD＝α,∠BCD＝90°+α,∴∠ADC＝90°－,∠BDC＝45°－,∴∠ADB＝∠ADC－∠BDC＝45°.②CE＝2BE－AD.证明:如图2,过点C作CG⊥CE,交EB的延长线于点G.∵BC＝CD,CE平分∠BCD,∴CE垂直平分BD,∴BE＝-25-基础过关7.3图形的平移、对称(折叠)、旋转与位似能力提升能力提升由①知∠ADB＝45°,∴∠EBD＝45°,∴∠FEB＝45°,∴∠G＝45°,∴CE＝CG,EG＝CE.易知△ACE≌△BCG(SAS),∴AE＝BG.∵EG＝BE+BG＝BE+AE＝BE+DE－AD＝2BE－AD,∴CE＝2BE－AD.图1图2