圆的对称性(第2课时)(课件)-2022-2023学年九年级数学上册同步精品课堂(苏科版)

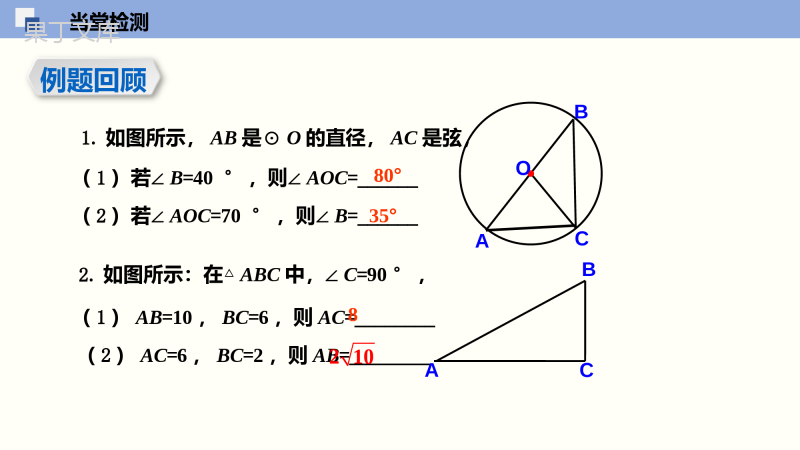
2.2圆的对称性第2课时垂径定理数学（苏科版）九年级上册第2—章对称图形圆学习目标1．理解垂直于弦的直径的性质和推论，并能应用它解决一些简单的计算、证明和作图问题.2．理解垂径定理并用垂径定理去解决圆相关的长度问题；3．掌握垂径定理的证明与应用；当堂检测例题回顾1.如图所示，AB是⊙O的直径，AC是弦，OABC（1）若∠B=40°，则∠AOC=______（2）若∠AOC=70°，则∠B=______2.如图所示：在△ABC中，∠C=90°，CAB（1）AB=10，BC=6，则AC=________（2）AC=6，BC=2，则AB=________80°35°8210导入新课欣赏图片思考：观察这些图片，你发现了什么？说一说你的发现。导入新课问题：你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥,是我国古代劳动人民勤劳与智慧的结晶．它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离)为7.2m。根据题目所给的数据，你可以求出赵州桥的半径吗？提问：赵州桥的半径是多少？讲授新课知识点一垂径定理及其推论可以发现：圆是轴对称图形.任何一条直径所在直线都是它的对称轴．问题1剪一个圆形纸片，沿着它的任意一条直径对折，重复几次，你发现了什么？由此你能得到什么结论？你能证明这个结论吗？讲授新课问题2如图,AB是⊙O的一条弦,直径CD⊥AB,垂足为E.你能发现图中有那些相等的线段和劣弧?为什么?线段:AE=BE弧:AC=BC,AD=BD⌒⌒⌒⌒理由如下：把圆沿着直径CD折叠时，CD两侧的两个半圆重合，点A与点B重合，AE与BE重合，AC和BC,AD与BD重合．⌒⌒⌒⌒·OABDEC讲授新课垂径定理·OABCDE垂直于弦的直径平分弦,并且平分弦所对的两条弧.∵CD是直径，CD⊥AB，∴AE=BE,⌒⌒AC=BC,⌒⌒AD=BD.归纳总结推导格式：温馨提示：垂径定理是圆中一个重要的定理,三种语言要相互转化,形成整体,才能运用自如.讲授新课想一想：下列图形是否具备垂径定理的条件？如果不是，请说明为什么？是不是，因为没有垂直是不是，因为CD没有过圆心ABOCDEOABCABOEABDCOE讲授新课垂径定理的几个基本图形：ABOCDEABOEDABODCABOC讲授新课思考：“不是直径”这个条件能去掉吗？如果不能，请举出反例.平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧.垂径定理的推论·OABCD特别说明：圆的两条直径是互相平分的.归纳总结典型例题如图所示，弦AB=8cm，CD是⊙O的直径，CD⊥AB，垂足为E，DE=2cm，求⊙O的直径CD的长.例1解连接OA.设OA=rcm，则OE=r-2(cm).∵CD⊥AB，由垂径定理得2ABAE==4(cm).2ABAE=讲授新课在Rt△AEO中，由勾股定理得+.222OA=OEAE解得r=5.∴CD=2r=10(cm).即.22(-2)4r=r+.22(-2)4r=r+练一练证明：圆的两条平行弦所夹的弧相等.已知：如图，在⊙O中，弦AB与弦CD平行.求证：=练习AC︵.BD︵证明作直径EF⊥AB，.AEBE︵︵∴又AB∥CD，EF⊥AB，∴EF⊥CD..CEDE︵︵∴，AECEBEDE︵︵︵︵因此.ACBD︵︵即AC︵.BD︵.AEBE︵︵.CEDE︵︵，AECEBEDE︵︵︵︵.ACBD︵︵练一练·ABCDOEF相等证明:作直径EF垂直于弦AB，由于AB//CD，因此EF⊥CD，由于EF⊥AB，因此，AE=BE，由于EF⊥CD，因此，CE=DE，从而AE-CE=BE-DE，即AC=BD.2.如果圆的两条弦互相平行，那么这两条弦所夹的弧相等吗？为什么？讲授新课知识点二垂径定理的实际应用例1、1400年前，我国隋朝建造的赵州石拱桥（如图）是圆弧形，它的跨度（即弧所对的弦长）为37.4m，拱高（即弧的中点到弦的距离）为7.2m，求桥拱所在圆的半径（结果精确到0.1m）.讲授新课ABAD21,7.184.3721在Rt△OAD中，由勾股定理，得：OA2=AD2+OD2，即R2=18.72+(R-7.2)2.解得R≈27.9（m）.答：桥拱所在圆的半径约为27.9m.解：如图，用表示桥拱，所在圆的圆心为O，半径为Rm，经过圆心O作弦AB的垂线OD，D为垂足，与相交于点C.根据垂径定理，D是AB的中点，C是的中点，CD就是拱高.由题设⌒AB⌒AB⌒AB⌒ABRD37.47.2OABCAB=37.4，CD=7.2，OD=OC-DC=R-7.2.ABAD21,7.184.3721练一练∴AC==56mm.226533-1.如图，在直径为130mm的圆形铁片上切下一块高为32mm的弓形铁片，求弓形的弦AB的长.C解：过O点作弦AB的平分线，交直线AB于点C，连结OA，OB，则OC⊥AB.∵OC=65-32=33mm，∴AB=2AC=112cm.226533-讲授新课在圆中有关弦长a,半径r,弦心距d（圆心到弦的距离），弓形高h的计算题时，常常通过连半径或作弦心距构造直角三角形，利用垂径定理和勾股定理求解.方法归纳涉及垂径定理时辅助线的添加方法弦a，弦心距d，弓形高h，半径r之间有以下关系：弓形中重要数量关系ABCDOhrd2222ardd+h=rOABC·2a2222ard当堂检测1.已知：如图，在⊙O中，AB是⊙O的直径，OA⊥CD于点P.求证：BC=BD.证明：OABCDP∵CD是⊙O的一条弦，直径AB⊥CD，由垂径定理，得：BC=BD.当堂检测2.已知⊙O的半径为13cm，一条弦的弦心距为5cm.求这条弦的长.解：由半径、弦心距、弦的一半可以围成一个直接三角形.∵直角三角形的斜边即半径长为13cm，一条直角边即弦心距为5cm，22135-∴另一条直角边长为=12cm.∴这条弦的长为24cm.22135-当堂检测证明：∵AM=BM，∴PQ⊥AB.3.已知：如图，⊙O的直径PQ分别交弦AB，CD于点M，N，AM=BM，AB∕∕CD.求证：DN=CN.连结OC、OD，∵OC=OD，∠OND=∠ONC，∵AB∕∕CD，∴PQ⊥CD.当堂检测4．如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，求⊙O的半径．·OABE解：在Rt△AEO中，∵OE⊥AB，∴AE=AB=×8=4.1212AO2=OE2+AE2.AO===5cm.22OEAE+2234+121222OEAE+2234+当堂检测5．如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB，OE⊥AC，垂足分别为D，E.求证：四边形ADOE是正方形．D·OABCE证明：∵OE⊥AC，OD⊥AB，AB⊥AC，∴四边形ADOE为矩形，又∵AC=AB∴AE=AD∴∠OEA=90°，∠EAD=90°，∠ODA=90°.AE=AC，AD=AB.12121212课堂小结垂径定理内容推论辅助线一条直线满足:①过圆心;②垂直于弦;③平分弦（不是直径）;④平分弦所对的优弧;⑤平分弦所对的劣弧.满足其中两个条件就可以推出其它三个结论（“知二推三”）垂直于弦的直径平分弦,并且平分弦所对的两条弧两条辅助线：连半径，作弦心距构造Rt△利用勾股定理计算或建立方程.基本图形及变式图形谢谢~