中考数学专题复习--抛物线中三角形面积的计算——铅垂法--课件

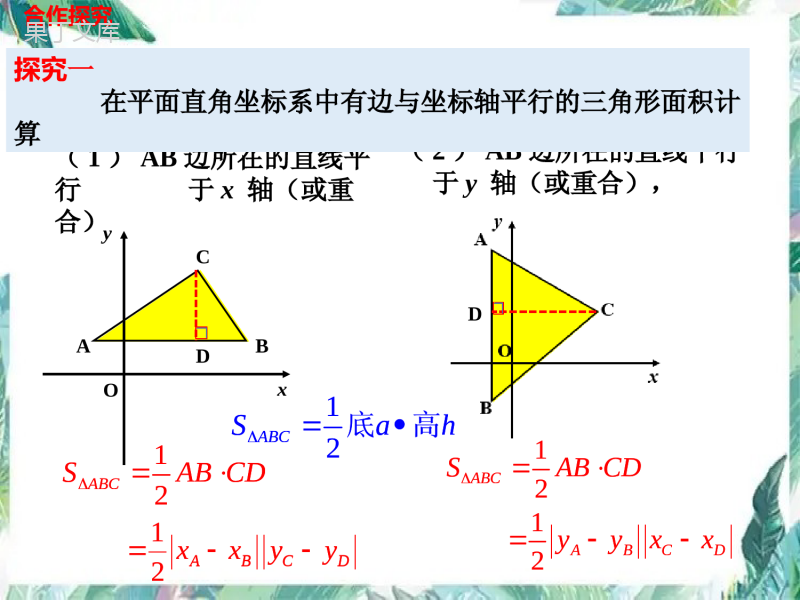
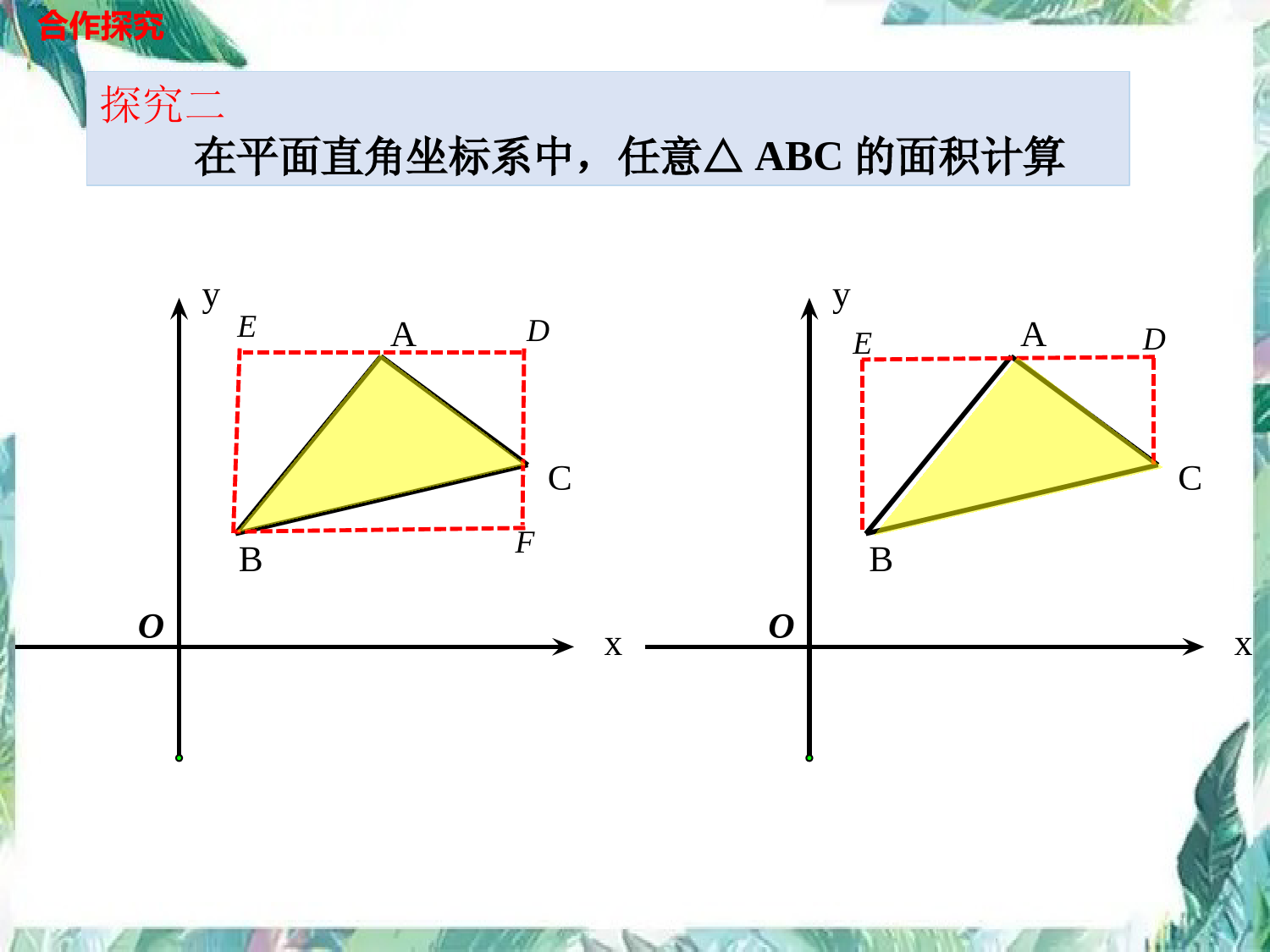
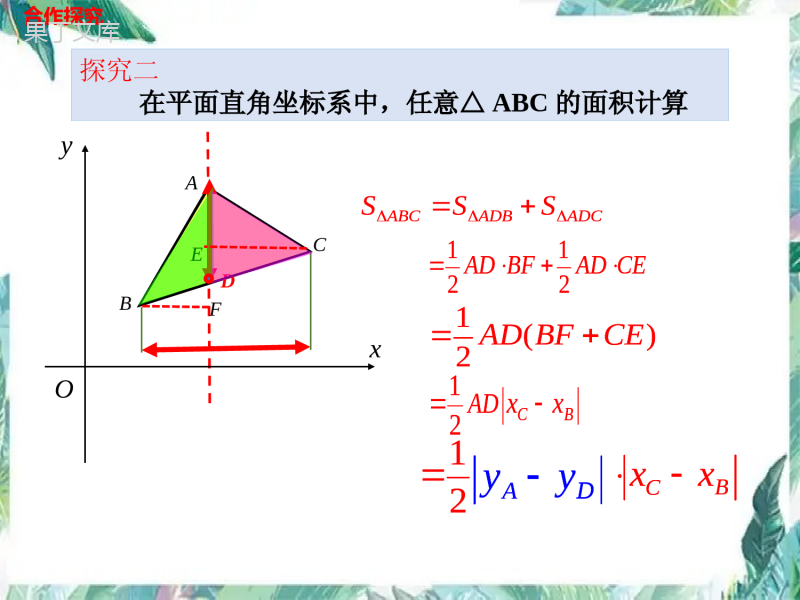
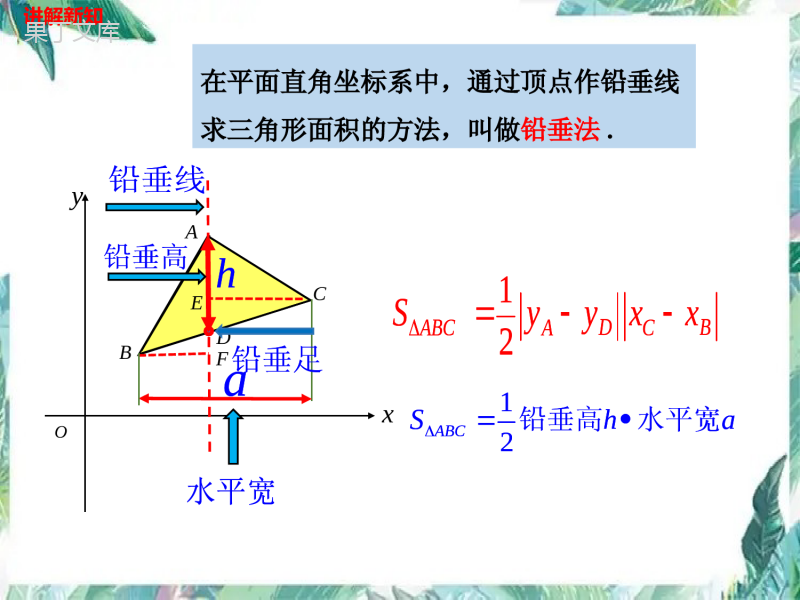
抛物线中三角形面积的计算--铅垂法中考数学专题（1）AB边所在的直线平行于x轴（或重合）12ABCSABCD12ABCSABCD合作探究ABCDOxy12ABCDxxyy12ABCDyyxx（2）AB边所在的直线平行于y轴（或重合），探究一在平面直角坐标系中有边与坐标轴平行的三角形面积计算D12ABCSah底高12ABCSABCD12ABCSABCD12ABCDxxyy12ABCDyyxx12ABCSah底高yxCBAOyxCBAO探究二在平面直角坐标系中，任意△ABC的面积计算DEF合作探究DEDxOyBCAEF合作探究ABCADBADCSSS1122ADBFADCE1()2ADBFCE12BCADxx探究二在平面直角坐标系中，任意△ABC的面积计算12BCxxDAyyABCADBADCSSS1122ADBFADCE1()2ADBFCE12BCADxx12BCxxDAyyxOyBCA在平面直角坐标系中，通过顶点作铅垂线求三角形面积的方法，叫做铅垂法.DEFha讲解新知12DBABCACSyyxx水平宽12ABCSha铅垂高水平宽铅垂高铅垂足铅垂线ha12DBABCACSyyxx水平宽12ABCSha铅垂高水平宽铅垂高铅垂足铅垂线如图,若由D作铅垂线交AC于点E,则△ACD的面积为.12ACDS12(5).4026小试牛刀4CAD（2，-5）-4E（2，-2）Oyx铅垂高水平宽.EDyyACxx612ACDS12(5).4026铅垂高水平宽.EDyyACxxDxyOCBA典例剖析3ACyx直线的解析式为如图，抛物线与轴交于A、B两点，223yxxx（1）若点D是抛物线的顶点，求△ACD的面积；A(3,0)12ACDS12(4)(30)2点D(1,-4)E(1，-2)03xy当时，2120230,1,3xxxx当y时，解得DxAC过点作轴的垂线交于点EE与轴交于点C，y2223(1)4yxxxACxxEDyy铅垂高水平宽(0,3)C点解：A(3,0)(0,3)C点D(1,-4)33ACyx直线的解析式为223yxxxA(3,0)12ACDS12(4)(30)2点D(1,-4)E(1，-2)03xy当时，2120230,1,3xxxx当y时，解得DxAC过点作轴的垂线交于点Ey2223(1)4yxxxACxxEDyy铅垂高水平宽(0,3)C点解：A(3,0)(0,3)C点D(1,-4)3xyODCBA典例剖析如图，抛物线与轴交于A、B两点，x与轴交于点C，y（2）若点D是抛物线上直线AC下方的一个动点,设△ACD的面积为S,点D的横坐标为t.试求出S关于t的函数关系式;2DxC解：（）过点作轴的垂线交A于点E12EDACSyyxx2,Dtttt-2-3_)点（（0<<3)，23922tt(,3),ttE223yxxE21(3)-(23)302ttt（）铅垂xy2DxC解：（）过点作轴的垂线交A于点E12EDACSyyxx2,Dtttt-2-3_)点（（0<<3)，23922tt(,3),ttE223yxx21(3)-(23)302ttt（）铅垂长郡文昌学校典例剖析如图，抛物线与轴交于A、B两点，x与轴交于点C.y（3）试求（2）中△ACD的面积S的最大值223yxx278且为23327()228t239322Stt解：（）xyODCBAEt（0<<3)，32a<0，32t当时，S有最大值，xy223yxx278且为23327()228t239322Stt解：（）t（0<<3)，32a<0，32t当时，S有最大值，归纳提升铅垂法求抛物线中两定一动点构成的三角形面积的一般步骤：（3）设表坐标：设动点D（4）计算面积：（2）求定直线：求过两定点的直线AC;（1）作铅垂线：过动点D作铅垂线;12Sha铅垂高水平宽xyODCBAE表铅垂足E2,)tatbtc（,)tktb（12Sha铅垂高水平宽2,)tatbtc（,)tktb（中考演练（2018年郴州中考）如图1，已知抛物线y=﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C点，点P是抛物线上在第一象限内的一个动点，且点P的横坐标为t．（1）求抛物线的表达式；（2）如图，设△PBC的面积为S，求S关于t的函数表达式；2PxBC（）过点作轴的垂线交于点D,3B(3),点C（0），，012PDBCSyyxx2,++3Pttt设点（-2）（0