2022年全国高考数学(新高考1卷)真题及答案解析

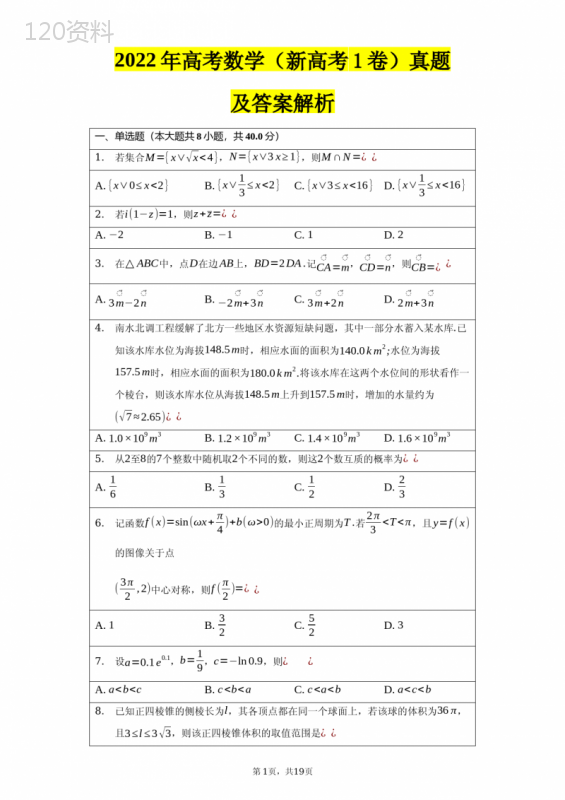
("2022年高考数学（新高考1卷）真题及答案解析一、单选题（本大题共8小题，共40.0分）1.若集合M={x∨√x<4}，N={x∨3x≥1}，则M∩N=¿¿A.{x∨0≤x<2}B.{x∨13≤x<2}C.{x∨3≤x<16}D.{x∨13≤x<16}2.若i(1−z)=1，则z+z=¿¿A.−2B.−1C.1D.23.在△ABC中，点D在边AB上，BD=2DA.记CA⃗=m⃗，CD⃗=n⃗，则CB⃗=¿¿A.3m⃗−2n⃗B.−2m⃗+3n⃗C.3m⃗+2n⃗D.2m⃗+3n⃗4.南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔148.5m时，相应水面的面积为140.0km2;水位为海拔157.5m时，相应水面的面积为180.0km2.将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148.5m上升到157.5m时，增加的水量约为(√7≈2.65)¿¿A.1.0×109m3B.1.2×109m3C.1.4×109m3D.1.6×109m35.从2至8的7个整数中随机取2个不同的数，则这2个数互质的概率为¿¿A.16B.13C.12D.236.记函数f(x)=sin(ωx+π4)+b(ω>0)的最小正周期为T.若2π30)上，过点B(0,−1)的直线交C于P，Q两点，则¿¿A.C的准线为y=−1B.直线AB与C相切C.¿OP∨⋅∨OQ∨¿OA2D.¿BP∨⋅∨BQ∨¿∨BA¿212.已知函数f(x)及其导函数f'(x)的定义域为R，记g(x)=f'(x).若f(32−2x)，g(2+x)均为偶函数，则¿¿A.f(0)=0B.g(−12)=0C.f(−1)=f(4)D.g(−1)=g(2)三、填空题（本大题共4小题，共20.0分）13.(1−yx)¿的展开式中x2y6的系数为¿用数字作答¿．14.写出与圆x2+y2=1和¿都相切的一条直线的方程．15.若曲线y=(x+a)ex有两条过坐标原点的切线，则a的取值范围是．16.已知椭圆C:x2a2+y2b2=1(a>b>0)，C的上顶点为A，两个焦点为F1，F2，离心率第2页，共19页为12，过F1且垂直于AF2的直线与C交于D，E两点，¿DE∨¿6，则△ADE的周长是．四、解答题（本大题共6小题，共70.0分）17.记Sn为数列{an}的前n项和，已知a1=1，{Snan}是公差为13的等差数列．(1)求{an}的通项公式;(2)证明：1a1+1a2+⋯+1an<2．18.记△ABC的内角A，B，C的对边分别为a，b，c，已知cosA1+sinA=sin2B1+cos2B．(1)若C=2π3，求B;(2)求a2+b2c2的最小值．19.如图，直三棱柱ABC−A1B1C1的体积为4，△A1BC的面积为2√2．(1)求A到平面A1BC的距离;(2)设D为A1C的中点，AA1=AB，平面A1BC⊥平面ABB1A1，求二面角A−BD−C的正弦值．20.一支医疗团队研究某地的一种地方性疾病与当地居民的卫生习惯¿卫生习惯分为良好和不够良好两类¿的关系，在已患该疾病的病例中随机调查了100例¿称为病例第3页，共19页组¿，同时在未患该疾病的人群中随机调查了100人¿称为对照组¿，得到如下数据：不够良好良好病例组4060对照组1090(1)能否有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异⋅(2)从该地的人群中任选一人，A表示事件“选到的人卫生习惯不够良好”，B表示事件“选到的人患有该疾病”，P(B∨A)P(B∨A)与P(B∨A)P(B∨A)的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标，记该指标为R．(i)证明：R=P(A∨B)P(A∨B)．P(A∨B)P(A∨B);(ii)利用该调查数据，给出P(A∨B)，P(A∨B)的估计值，并利用(i)的结果给出R的估计值．附：K2=n¿¿，P(K2≥k)0.0500.0100.001k3.8416.63510.82821.已知点A(2,1)在双曲线C:x2a2−y2a2−1=1(a>1)上，直线l交C于P，Q两点，直线AP，AQ的斜率之和为0．(1)求l的斜率;(2)若tan∠PAQ=2√2，求△PAQ的面积．已知函数f(x)=ex−ax和g(x)=ax−lnx有相同的最小值．(1)求a;(2)证明：存在y=b直线，其与两条曲线y=f(x)和y=g(x)共有三个不同的交点，并且从左到右的三个交点的横坐标成等差数列．答案和解析1.【答案】D【解析】第4页，共19页【分析】本题主要考查了集合的交集运算，属于基础题．【解答】解：因为M={x∨0≤x<16}，N={x∨x≥13}，故M∩N={x∨13≤x<16}．2.【答案】D【解析】【分析】本题考查了复数代数形式的四则运算及共轭复数，属基础题．【解答】解：z=1+i，z+z=1+i+1−i=2．3.【答案】B【解析】【分析】本题主要考查向量的加减及数乘运算，属于基础题．【解答】解：CD⃗=23CA⃗+13CB⃗，CB⃗=3CD⃗−2CA⃗=−2m⃗+3n⃗．4.【答案】C【解析】【分析】本题考查了棱台的体积公式的应用，属于基础题．【解答】解：依据棱台的体积公式V=13⋅¿¿13⋅(140000000+180000000+√14000000×18000000)×9≈1.4×109m3．5.【答案】D【解析】第5页，共19页【分析】本题考查了古典概型及其计算，涉及组合数公式、对立事件的概率公式，属基础题．【解答】解：由题可知，总的取法有C72=21种，不互质的数对情况有：两个偶数，3和6．所以两个数互质的概率为P=1−C42+121=23．6.【答案】A【解析】【分析】本题主要考查三角函数的周期性和对称性，属于中档题．【解答】解：由题可知：T=2πω∈(2π3,π)，所以ω∈(2,3)．又因为y=f(x)的图像关于点(3π2,2)中心对称，所以b=2，且f(3π2)=sin(ω×3π2+π4)+b=2．所以ω=23(k−14)，k∈Z，所以ω=52.所以f(x)=sin(52x+π4)+2.所以f(π2)=1．7.【答案】C【解析】【分析】本题考查了利用导数比较大小，关键是构造合适的函数，考查了运算能力，属于较难题．【解答】解：a=0.1e0.1，b=0.11−0.1，c=−ln(1−0.1)，①lna−lnb=0.1+ln(1−0.1)，令f(x)=x+ln(1−x),x∈¿,第6页，共19页则f'(x)=1−11−x=−x1−x<0，故f(x)在¿上单调递减，可得f(0.1)0，所以k(x)在¿上单调递增，可得k(x)>k(0)>0，即g'(x)>0，所以g(x)在¿上单调递增，可得g(0.1)>g(0)=0，即a−c>0，所以a>c．故c0⇒x←√33或x>√33；f'(x)<0⇒−√330，f(√33)=√39−√33+1=1−2√39>0，所以f(x)仅有1个零点¿如图所示¿，故B错;第9页，共19页又f(−x)=−x3+x+1⇒f(−x)+f(x)=2，所以f(x)关于(0,1)对称，故C正确;对于D选项，设切点P(x0,y0)，在P处的切线为y−(x03−x0+1)=(3x02−1)(x−x0)，即y=(3x02−1)x−2x03+1，若y=2x是其切线，则{3x02−1=2−2x03+1=0，方程组无解，所以D错．11.【答案】BCD【解析】【分析】本题考查了直线与抛物线的位置关系，属较难题．【解答】解：点A(1,1)在抛物线C:x2=2py(p>0)上，即1=2p⇒C:x2=y，所以准线为y=−14，所以A错;直线AB:y=2x−1代入x2=y得：x2−2x+1=0⇒¿，所以AB与C相切，故B正确．由题知直线PQ的斜率一定存在，则可设直线PQ:y=kx−1，P(x1,y1)，Q(x2,y2)，则{y=kx−1y=x2⇒x2−kx+1=0，Δ=k2−4>0⇒k←2或k>2，第10页，共19页此时{x1+x2=kx1x2=1,¿¿OP∨⋅∨OQ∨¿√(x12+y12)(x22+y22)=√(y1+y12)(y2+y22)=√¿¿，故C正确;¿BP∨⋅∨BQ∨¿√1+k2∨x1−0∨√1+k2∨x2−0∨¿(1+k2)∨x1x2∨¿(1+k2)>5=¿BA¿2，故D正确．12.【答案】BC【解析】【分析】本题主要考查导函数与原函数的关系，函数的对称性及奇偶性，属于难题．【解答】解：由f(32−2x)为偶函数可知f(x)关于直线x=32对称，由g(2+x)为偶函数可知g(x)关于直线x=2对称，结合g(x)=f'(x)，根据g(x)关于直线x=2对称可知f(x)关于点(2,t)对称，第11页，共19页根据f(x)关于直线x=32对称可知：g(x)关于点(32,0)对称，综上，函数f(x)与g(x)均是周期为2的周期函数，所以有f(0)=f(2)=t，所以A不正确;f(−1)=f(1)，f(4)=f(2)，f(1)=f(2)，故f(−1)=f(4)，所以C正确．g(−12)=g(32)=0，g(−1)=g(1)，所以B正确;又g(1)+g(2)=0，所以g(−1)+g(2)=0，所以D不正确．13.【答案】−28【解析】【分析】本题考查二项展开式的特定项与特定项的系数，属于基础题．【解答】解：因为¿展开式的通项Tr+1=C8rx8−ryr，令r=5，则x3y5的系数为C85=56；令r=6，则x2y6的系数为C86=28，所以x2y6的系数为−56+28=−28．14.【答案】x+1=07x−24y−25=03x+4y−5=0¿填一条即可¿【解析】【分析】本题考查了圆与圆的公切线问题，涉及圆与圆的位置关系、点到直线的距离等知识，属较难题．【解答】解：方法1:显然直线的斜率不为0，不妨设直线方程为x+by+c=0，于是¿c∨¿√1+b2=1¿，¿3+4b+c∨¿√1+b2=4¿．故c2=1+b2①，¿3+4b+c∨¿∨4c∨.于是3+4b+c=4c或3+4b+c=−4c，再结合①解得{b=0c=1或{b=−247c=−257或{b=43c=−53，所以直线方程有三条，分别为第12页，共19页x+1=0，7x−24y−25=0，3x+4y−5=0．¿填一条即可¿方法2:设圆x2+y2=1的圆心O(0,0)，半径为r1=1，圆¿的圆心C(3,4)，半径r2=4，则¿OC∨¿5=r1+r2，因此两圆外切，由图像可知，共有三条直线符合条件，显然x+1=0符合题意；又由方程¿和x2+y2=1相减可得方程3x+4y−5=0，即为过两圆公共切点的切线方程，又易知两圆圆心所在直线OC的方程为4x−3y=0，直线OC与直线x+1=0的交点为(−1,−43)，设过该点的直线为y+43=k(x+1)，则k−43√k2+1=1，解得k=724，从而该切线的方程为7x−24y−25=0.¿填一条即可¿15.【答案】(−∞,−4)∪(0,+∞)【解析】【分析】本题主要考查过曲线外一点的切线问题，属于中档题．【解答】第13页，共19页解：y'=(x+a+1)ex，设切点为(x0,y0)，故y0x0=(x0+a+1)ex0，即(x0+a)ex0x0=(x0+a+1)ex0.由题意可得，方程x+a=x(x+a+1)在(−∞,0)∪(0,+∞)上有两个不相等的实数根.化简得，x2+ax−a=0，△=a2+4a>0，解得a←4或a>0，显然此时0不是根，故满足题意．16.【答案】13【解析】【分析】本题主要考查了直线与椭圆的位置关系的应用、椭圆的定义以及椭圆中的弦长问题，考查了运算求解能力，属于中档题．【解答】解：由椭圆离心率为12，可得a=2c，则b=√a2−c2=√3c，则C：x24c2+y23c2=1，A(0,√3c)，F1(−c,0)，F2(c,0)，易得lAF2：y=−√3x+√3c，lED：y=√33(x+c)，可解得AF2与DE的交点M(c2,√3c2)，故直线DE垂直平分AF2，即EA=EF2，DA=DF2，第14页，共19页又{x24c2+y23c2=1y=√33(x+c)⇒13x2+8cx−32c2=0⇒{xD+xE=−8c13xDxE=−32c213∴∨DE∨¿√1+13∨xD−xE∨¿6⇒¿，所以△ADE的周长AD+AE+DE=DF2+EF2+DF1+EF1=4a=8c=13．17.【答案】解：(1)Snan=S1a1+13(n−1)=n+23⇒Sn=n+23an①;∴Sn+1=n+33an+1②;由②−①得：an+1=n+33an+1−n+23an⇒an+1an=n+2n;∴当n⩾2且n∈N¿时，ana1=anan−1⋅an−1an−2⋯a3a2⋅a2a1=n+1n−1⋅nn−2⋯53⋅42⋅31=(n+1)n2⇒an=n(n+1)2，又a1=1也符合上式，因此an=n(n+1)2(n∈N¿);(2)∵1an=2n(n+1)=2(1n−1n+1)，∴1a1+1a2+⋯+1an=2(11−12+12−13+⋯+1n−1n+1)=2(1−1n+1)<2，即原不等式成立．【解析】本题考查了数列与不等式，涉及裂项相消法求和、等差数列的通项公式、根据数列的递推公式求通项公式等知识，属中档题．18.【答案】解：(1)∵cosA1+sinA=sin2B1+cos2B，∴cos2A2−sin2A2cos2A2+sin2A2+2sinA2cosA2=2sinBcosB1+2cos2B−1且cosB≠0，第15页，共19页∴cosA2−sinA2cosA2+sinA2=sinBcosB∴1−tanA21+tanA2=tanB，∴tan(π4−A2)=tanB，又A，B∈(0,π)，π4−A2∈(−π4,π4)，∴π4−A2=B．又∵C=2π3，∴A+B=π3，∴B=π6．(2)由正弦定理asinA=bsinB=csinC，得a2+b2c2=sin2A+sin2Bsin2C=sin2A+sin2(π4−A2)sin2(A+π4−A2)1−cos2A2+1−cos2(π4−A2)21−cos2(A+π4−A2)2=1−cos2A+1−sinA1+sinA=2sin2A−sinA+11+sinA，{A∈(0,π)π4−A2=B∈(0,π)⇒A∈(0,π2)，令t=1+sinA∈(1,2)，则y=2¿¿，t∈(1,2)，y=2t−5+4t在t∈(1,√2)时递减，在t∈(√2,2)时递增，因此t=√2时，ymin=4√2−5．【解析】本题主要考查三角恒等变换的综合应用及利用余弦定理和对勾函数解决最值问题，属于中档题．19.【答案】解：(1)设A到平面A1BC的距离为d，因为直三棱柱ABC−A1B1C1的体积为4，即可得S△ABC·AA1=4，第16页，共19页故VA1−ABC=13S△ABC·AA1=43，又VA1−ABC=VA−A1BC=13S△A1BC·d=13×2√2×d=43，解得d=√2，所以A到平面A1BC的距离为√2；(2)连接AB1，因为直三棱柱ABC−A1B1C1中，AA1=AB，故AA1B1B为正方形，即AB1⊥A1B，又平面A1BC⊥平面ABB1A1，平面A1BC∩平面ABB1A1=A1B，AB1⊂平面ABB1A1，故AB1⊥平面A1BC，所以AB1⊥BC，又因为AA1⊥BC，AB1,AA1⊂平面ABB1A1，且AB1∩AB1=A，故BC⊥平面ABB1A1，则BC⊥AB，所以BB1,AB,BC三条直线两两垂直，故如图可以以B为原点建立空间直角坐标系，设AA1=AB=a，BC=b，则A1B=√2a，第17页，共19页由条件可得{12a×b×a=412×√2a×b=2√2，解得{a=2b=2,则B(0,0,0)，C(2,0,0)，A(0,2,0)，A1(0,2,2)，A1C的中点D(1,1,1)，所以BA⃗=(0,2,0)，BD⃗=(1,1,1)，BC⃗=(2,0,0)设平面ABD的一个法向量为n1⃗=(x,y,z)，{n1⃗⋅BA⃗=0n1⃗⋅BD⃗=0⇒{2y=0x+y+z=0，取n1⃗=(1,0,−1)，同理可求得平面BCD的一个法向量为n2⃗=(0,1,−1)所以¿cos¿=¿n1⃗·n2⃗∨¿n1⃗·n2⃗=12¿，所以二面角A−BD−C的正弦值为√32．【解析】本题考查了平面与平面所成角的空间向量求法、点到面的距离的几何求法、几何体的体积公式，考查了空间中的垂直关系的证明与应用，属于中档题．20.【答案】解：(1)得到2×2联表如下：不够良好良好总计病例组4060100对照组1090100总计50150200∵K2=200׿¿∴有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异;(2)(i)证明：∵P(B∨A)=P(BA)P(A)，P(B∨A)=P(BA)P(A)，第18页，共19页P(B∨A)=P(BA)P(A)，P(B∨A)=P(BA)P(A)，∴R=P(B∨A)P(B∨A)÷P(B∨A)P(B∨A)=P(BA)P(A)P(BA)P(A)÷P(BA)P(A)P(BA)P(A)=P(BA)P(BA)·P(BA)P(BA)又∵P(A∨B)=P(AB)P(B)，P(A∨B)=P(AB)P(B)，P(A∨B)=P(AB)P(B)，P(A∨B)=P(AB)P(B)，∴P(A∨B)P(A∨B)·P(A∨B)P(A∨B)=P(AB)P(B)P(AB)P(B)·P(AB)P(B)P(AB)P(B)=P(AB)P(AB)·P(AB)P(AB)=P(BA)P(BA)·P(BA)P(BA)，∴R=P(A∨B)P(A∨B)·P(A∨B)P(A∨B);(ii)∵P(A∨B)=P(AB)P(B)=40100=25，P(A∨B)=P(AB)P(B)=60100=35，P(A∨B)=P(AB)P(B)=90100=910，P(A∨B)=P(AB)P(B)=10100=110∴P(A∨B)P(A∨B)⋅P(A∨B)P(A∨B)=2535×910110=6∴R=P(A∨B)P(A∨B)．P(A∨B)P(A∨B)=6即P(A∨B)=25，P(A∨B)=110，R的估计值为6．【解析】本题考查了独立性检验和条件概率的计算，属中档题．21.【答案】解：(1)将点A代入双曲线方程得4a2−1a2−1=1，化简得a4−4a2+4=0第19页，共19页得：a2=2，故双曲线方程为x22−y2=1;由题显然直线l的斜率存在，设l:y=kx+m，设P(x1,y1)，Q(x2,y2)，则联立直线与双曲线得：(2k2−1)x2+4kmx+2m2+2=0，△>0，故x1+x2=−4km2k2−1，x1x2=2m2+22k2−1，kAP+kAQ=y1−1x1−2+y2−1x2−2=kx1+m−1x1−2+kx2+m−1x2−2=0，化简得：2kx1x2+(m−1−2k)(x1+x2)−4(m−1)=0，故2k(2m2+2)2k2−1+(m−1−2k)(−4km2k2−1)−4(m−1)=0，即(k+1)(m+2k−1)=0，而直线l不过A点，故k=−1．(2)设直线AP的倾斜角为α，由tan∠PAQ=2√2，得tan∠PAQ2=√22，由2α+∠PAQ=π，得kAP=tanα=√2，即y1−1x1−2=√2，联立y1−1x1−2=√2，及x122−y12=1得x1=10−4√23，y1=4√2−53，同理，x2=10+4√23，y2=−4√2−53，故x1+x2=203，x1x2=689而¿AP∨¿√3∨x1−2∨¿，¿AQ∨¿√3∨x2−2∨¿，第20页，共19页由tan∠PAQ=2√2，得sin∠PAQ=2√23，故S△PAQ=12∨AP∨¿AQ∨sin∠PAQ=√2∨x1x2−2(x1+x2)+4∨¿16√29．【解析】本题主要考查直线与双曲线的位置关系及双曲线中面积问题，属于难题．22.【答案】解：(1)由题知f'(x)=ex−a，g'(x)=a−1x，①当a≤0时，f'(x)>0，，g'(x)<0，则两函数均无最小值，不符题意;②当a>0时，f(x)在(−∞,lna)单调递减，在(lna,+∞)单调递增；g(x)在(0,1a)单调递减，在(1a,+∞)单调递增；故f¿，g¿，所以a−alna=1−ln1a，即lna−a−1a+1=0，令p(a)=lna−a−1a+1，则p'(a)=1a−2¿¿，则p(a)在(0,+∞)单调递增，又p(1)=0，所以a=1．(2)由(1)知，f(x)=ex−x，g(x)=x−lnx，且f(x)在(−∞,0)上单调递减，在(0,+∞)上单调递增；g(x)在(0,1)上单调递减，在(1,+∞)上单调递增，且f¿．①b<1时，此时f¿，显然y=b与两条曲线y=f(x)和y=g(x)共有0个交点，不符合题意；②b=1时，此时f¿，故y=b与两条曲线y=f(x)和y=g(x)共有2个交点，交点的横坐标分别为0和1；③b>1时，首先，证明y=b与曲线y=f(x)有2个交点，即证明F(x)=f(x)−b有2个零点，F'(x)=f'(x)=ex−1，所以F(x)在(−∞,0)上单调递减，在(0,+∞)上单调递增，又因为F(−b)=e−b>0，F(0)=1−b<0，F(b)=eb−2b>0，第21页，共19页¿令t(b)=eb−2b，则t'(b)=eb−2>0，t(b)>t(1)=e−2>0¿所以F(x)=f(x)−b在(−∞,0)上存在且只存在1个零点，设为x1，在(0,+∞)上存在且只存在1个零点，设为x2．其次，证明y=b与曲线和y=g(x)有2个交点，即证明G(x)=g(x)−b有2个零点，G'(x)=g'(x)=1−1x，所以G(x)(0,1)上单调递减，在(1,+∞)上单调递增，又因为G(e−b)=e−b>0，G(0)=1−b<0，G(2b)=b−ln2b>0，¿令μ(b)=b−ln2b，则μ'(b)=1−1b>0，μ(b)>μ(1)=1−ln2>0¿所以G(x)=g(x)−b在(0,1)上存在且只存在1个零点，设为x3，在(1,+∞)上存在且只存在1个零点，设为x4．再次，证明存在b，使得x2=x3:因为F(x2)=G(x3)=0，所以b=ex2−x2=x3−lnx3，若x2=x3，则ex2−x2=x2−lnx2，即ex2−2x2+lnx2=0，所以只需证明ex−2x+lnx=0在(0,1)上有解即可，即φ(x)=ex−2x+lnx在(0,1)上有零点，因为φ(1e3)=e1e3−2e3−3<0，φ(1)=e−2>0，所以φ(x)=ex−2x+lnx在(0,1)上存在零点，取一零点为x0，令x2=x3=x0即可，此时取b=ex0−x0则此时存在直线y=b，其与两条曲线y=f(x)和y=g(x)共有三个不同的交点，最后证明x1+x4=2x0，即从左到右的三个交点的横坐标成等差数列，因为F(x1)=F(x2)=F(x0)=0=G(x3)=G(x0)=G(x4)第22页，共19页所以F(x1)=G(x0)=F(lnx0)，又因为F(x)在(−∞,0)上单调递减，x1<0，00即ex0>1，x1>1，所以x4=ex0，又因为ex0−2x0+lnx0=0，所以x1+x4=ex0+lnx0=2x0，即直线y=b与两条曲线y=f(x)和y=g(x)从左到右的三个交点的横坐标成等差数列．【解析】本题主要考查了利用导数研究函数单调性、最值，函数零点问题，考查了分类讨论思想，属于难题．第23页，共19页",)