('双曲线及其标准方程自主预习·探新知情景引入通过前面的学习,我们已经知道,平面内与两个定点距离之和为常数(大于两定点间的距离)的点的轨迹是椭圆.如果我们把上述椭圆定义中的“距离的和”改为“距离的差”,那么点的轨迹还存在吗?如果存在,点的轨迹又是什么呢?它的方程又是怎样的呢?新知导学1.双曲线的定义(1)在平面内到两个定点F1、F2距离之__差__的绝对值等于定值2a(大于0且小于F1F2)的点的轨迹叫做双曲线.这两个定点叫做双曲线的__焦点__,两焦点之间的距离叫做双曲线的__焦距__.(2)定义中为何强调“绝对值”和“0<2aF1F2,则动点的轨迹是__不存在__.②双曲线定义中应注意关键词“__绝对值__”,若去掉定义中“__绝对值__”三个字,动点轨迹只能是__双曲线的一支__.2.双曲线方程焦点在x轴上的双曲线的标准方程为__-=1(a>0,b>0)__,焦点在y轴上的双曲线的标准方程为__-=1(a>0,b>0)__.其中在双曲线的标准方程中a、b、c的关系为__a2+b2=c2__.3.椭圆、双曲线的标准方程的区别和联系椭圆双曲线定义MF1+MF2=2a定义MF1-MF2=±2a因为a>c>0,所以令a2-c2=b2(b>0)因为00)+=1或+=1(a>b>0)-=1或-=1(a>0,b>0,a不一定大于b)预习自测1.双曲线x2-=1的焦点坐标是(B)A.(0,±2)B.(±2,0)C.(0,±)D.(±,0)2.已知两定点F1(-3,0)、F2(3,0),在满足下列条件的平面内动点P的轨迹中,是双曲线的是(A)A.PF1-PF2=5B.PF1-PF2=6C.PF1-PF2=7D.PF1-PF2=0[解析]A中,∵F1F2=6,∴PF1-PF2=5F1F2,∴动点P的轨迹不存在;D中,∵PF1-PF2=0,即PF1=PF2,根据线段垂直平分线的性质,动点P的轨迹是线段F1F2的垂直平分线,故选A.3.双曲线-=1的焦距为(D)A.3B.4C.3D.4[解析]c===2,焦距2c=4.4.(2019-2020学年辽宁葫芦岛协作校考试)若方程+=1表示焦点在x轴上的双曲线,则m的取值范围是__(4,+∞)__.[解析]由题意可得,解得m>4.故答案为(4,+∞).5.P是双曲线x2-y2=16的左支上一点,F1,F2分别是左、右焦点,则PF1-PF2=__-8__.[解析]双曲线方程为-=1,∴a=4,∴PF1-PF2=2a=8,又∵P在左支上,F1为左焦点,∴PF1-PF2=-8.互动探究·攻重难互动探究解疑命题方向❶双曲线的定义典例1已知动圆M与圆C1:(x+4)2+y2=2外切,与圆C2:(x-4)2+y2=2内切,求动圆圆心M的轨迹方程.[思路分析]利用两圆内、外切的充要条件找出M点所满足的几何条件,结合双曲线定义求解.[规范解答]设动圆M的半径为r,则由已知MC1=r+,MC2=r-,∴MC1-MC2=2.又C1(-4,0)、C2(4,0),∴C1C2=8,∴20,cosθ<0,故选A.┃┃跟踪练习2__■已知方程-=1表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是(A)A.(-1,3)B.(-1,)C.(0,3)D.(0,)[解析]由题意得(m2+n)(3m2-n)>0,解得-m20,b>0),代入点的坐标,解方程组求出a2、b2,也可以直接设方程Ax2+By2=1(A>0,B<0).[规范解答](1)由已知得,c=5,2a=8,即a=4.∵c2=a2+b2,∴b2=c2-a2=52-42=9.∵焦点在x轴上,∴所求的双曲线标准方程是-=1.(2)设双曲线方程为mx2+ny2=1(m>0,n<0),则,∴,∴双曲线方程为-=1.『规律总结』利用待定系数法求双曲线标准方程的步骤如下:(1)定位置:根据条件判定双曲线的焦点在x轴上还是在y轴上,不能确定时应分类讨论;(2)设方程:根据焦点位置,设方程为-=1或-=1(a>0,b>0),焦点不定时,亦可设为mx2+ny2=1(m·n<0);(3)寻关系:根据已知条件列出关于a、b(或m、n)的方程组;(4)得方程:解方程组,将a、b、c(或m、n)的值代入所设方程即为所求.┃┃跟踪练习3__■根据下列条件,求双曲线的标准方程.(1)与双曲线-=1有相同的焦点,且经过点(3,2);(2)过点P(3,),Q(-,5)且焦点在坐标轴上.[解析](1)因为焦点相同,所以所求双曲线的焦点也在x轴上,且c2=a2+b2=16+4=20,利用待定系数法求解,或设出统一方程求解.(2)已知双曲线经过两个已知点,因焦点位置不确定,需分类讨论求解,或设出一般方程求解.(1)解法一:∵焦点相同,∴设所求双曲线的标准方程为-=1(a>0,b>0),∴c2=16+4=20,即a2+b2=20,①∵双曲线经过点(3,2),∴-=1.②由①②得a2=12,b2=8,∴双曲线的标准方程为-=1.解法二:设所求双曲线的方程为-=1(-4<λ<16).∵双曲线过点(3,2),∴-=1,解得λ=4或λ=-14(舍去).∴双曲线的标准方程为-=1.(2)解法一:当焦点在x轴上时,设标准方程为-=1(a>0,b>0).∵点P,Q在双曲线上,∴此方程无解.当焦点在y轴上时,设标准方程为-=1(a>0,b>0).∵点P,Q在双曲线上,∴解得∴双曲线的标准方程为-=1.解法二:设双曲线的方程为+=1,mn<0.∵点P,Q在双曲线上,∴解得∴双曲线的标准方程为-=1.命题方向❹焦点三角形问题典例4设双曲线-=1,F1、F2是其两个焦点,点P在双曲线右支上.(1)若∠F1PF2=90°,求△F1PF2的面积;(2)若∠F1PF2=60°时,△F1PF2的面积是多少?若∠F1PF2=120°时,△F1PF2的面积又是多少?[思路分析]由于三角形面积S△F1PF2=PF1·PF2·sinθ,所以只要求出PF1·PF2即可.因此可考虑用双曲线定义及余弦定理求出PF1·PF2.[规范解答](1)由双曲线方程知a=2,b=3,c=,设PF1=r1,PF2=r2(r1>r2),如图所示.由双曲线定义,有r1-r2=2a=4,两边平方得r+r-2r1r2=16.∵∠F1PF2=90°,∴r+r=4c2=4×()2=52.∴2r1r2=52-16=36,∴S△F1PF2=r1r2=9.(2)若∠F1PF2=60°,在△F1PF2中,由余弦定理得F1F22=r+r-2r1r2cos60°=(r1-r2)2+r1r2,而r1-r2=4,F1F2=2,∴r1r2=36.于是S△F1PF2=r1r2sin60°=×36×=9.同理可求得若∠F1PF2=120°时,S△F1PF2=3.『规律总结』双曲线中的焦点三角形双曲线上的点P与其两个焦点F1,F2连接而成的三角形PF1F2称为焦点三角形.令PF1=r1,PF2=r2,∠F1PF2=θ,因F1F2=2c,所以有(1)定义:r1-r2=2a.(2)余弦公式:4c2=r+r-2r1r2cosθ(3)面积公式:S△PF1F2=r1r2sinθ.一般地,在△PF1F2中,通过以上三个等式,求问题就会顺利解决.┃┃跟踪练习4__■设P为双曲线-=1上一点,F1,F2是该双曲线的两个焦点,若∠F1PF2=60°,则△PF1F2的面积为__9__.[解析]由双曲线-=1知:a=4,b=3,故c==5,所以F1F2=2c=10.又由双曲线的定义,得PF1-PF2=8,两边平方,得PF12+PF22-2PF1·PF2=64,①在△PF1F2中,由余弦定理,得F1F22=PF12+PF22-2PF1PF2cos60°,即PF12+PF22-PF1PF2=100,②①-②,得PF1PF2=36,所以S△PF1F2=PF1·PF2sin60°=×36×=9.故填9.命题方向❺双曲线的实际应用典例5相距2000m的两个哨所A、B,听到远处传来的炮弹爆炸声.已知当时的声速是330m/s,在A哨所听到爆炸声的时间比在B哨所听到时间迟4s,试判断爆炸点在什么样的曲线上,并求出曲线的方程.[思路分析]爆炸点与哨所A、B的“距离差”等于声速乘以两哨所听到爆炸声的“时间差”,且爆炸点距B哨所较近.[规范解答]设爆炸点为P,由已知可得PA-PB=330×4=1320>0.因为AB=2000>1320,所以点P在以A、B为焦点的双曲线的靠近B处的那一支上.建立如图平面直角坐标系,使A、B两点在x轴上,线段AB的中点为坐标原点.由2a=1320,2c=2000得,a=660,c=1000,b2=c2-a2=564400.因此,点P所在曲线的方程是-=1(x>0).『规律总结』解答实际应用问题时,要注意先将实际问题数学化,条件中有两定点,某点与这两定点的距离存在某种联系,解题时先画出图形,分析其关系,看是否与椭圆、双曲线的定义有关,再确定解题思路、步骤.┃┃跟踪练习5__■A、B、C是我方三个炮兵阵地,A在B正东6km,C在B正北偏西30°,相距4km,P为敌炮阵地,某时刻A处发现敌炮阵地的某种信号,由于B、C两地比A距P地远,因此经过4s后,B、C才同时发现这一信号,此信号的传播速度为1km/s,A若炮击P地,则炮击的方向角是__北__(南、北)偏__东__(东、西)__30__度.[解析]如图,以直线BA为x轴,线段BA的中垂线为y轴建立坐标系,则B(-3,0)、A(3,0)、C(-5,2).因为PB=PC,所以点P在线段BC的垂直平分线上.因为kBC=-,BC中点D(-4,),所以直线PD:y-=(x+4).①又PB-PA=4,故P在以A、B为焦点的双曲线右支上.设P(x,y),则双曲线方程为-=1(x≥0)②联立①、②式,得x=8,y=5,所以P(8,5).因此kPA==.故炮击的方向角为北偏东30°.故答案为:北;东;30.学科核心素养双曲线的其他形式(1)双曲线的一般方程:当ABC≠0时,方程Ax2+By2=C可以变形为+=1,由此可以看出方程Ax2+By2=C表示双曲线的充要条件是ABC≠0,且A,B异号.此时称方程Ax2+By2=C为双曲线的一般方程.利用一般方程求双曲线的标准方程时,可以将其设为Ax2+By2=1(AB<0),将其化为标准方程,即+=1.因此,当A>0时,表示焦点在x轴上的双曲线;当B>0时,表示焦点在y轴上的双曲线.(2)共焦点的双曲线系方程:与双曲线-=1(a>0,b>0)有公共焦点的双曲线的方程为-=1(a>0,b>0);与双曲线-=1(a>0,b>0)有公共焦点的双曲线的方程为-=1(a>0,b>0).典例6下列各选项中,与-=1共焦点的双曲线是(C)A.+=1B.-=1C.-=1D.+=1[规范解答]方法一:因为所求曲线为双曲线,所以可排除选项A,D;又双曲线-=1的焦点在x轴上,所以排除选项B.方法二:与-=1共焦点的双曲线系方程为-=1,对比四个选项中的曲线方程,发现只有选项C中的方程符合条件(此时λ=-2).故选C.┃┃跟踪练习6__■与双曲线-=1有相同焦点,且过点的双曲线方程为__-=1__.[解析]设所求双曲线的方程为-=1(-64<λ<36).将x=10,y=代入方程,得-=1,解得λ=-4或λ=(舍去).故所求双曲线的方程为-=1.易混易错警示典例7已知双曲线8kx2-ky2=8的一个焦点为(0,3),求k的值.[错解]将双曲线方程化为标准方程-=1.因为焦点在y轴上,所以a2=,b2=,所以c===3,即=9,所以k=.[辨析]上述解法有两处错误:一是a2、b2确定错误,应该是a2=-,b2=-;二是a、b、c的关系式用错了.在双曲线中应为c2=a2+b2.[正解]将双曲线方程化为kx2-y2=1,即-=1.因为一个焦点是(0,3),所以焦点在y轴上,所以c=3,a2=-,b2=-,所以a2+b2=--=-=c2=9.所以k=-1.课堂达标·固基础1.椭圆+=1与双曲线-=1有相同的焦点,则a的值是(B)A.B.1C.1或-2D.1或[解析]由题意得4-a2=a+2,∴a2+a-2=0,∴a=1或-2(舍去)故选B.2.已知双曲线的两个焦点分别为F1(-,0),F2(,0),P是双曲线上的一点(a>0),且PF1⊥PF2,PF1·PF2=2,则双曲线的标准方程是(D)A.-=1B.-=1C.x2-=1D.-y2=1[解析]由题意知c=,∵PF1⊥PF2,∴在△ABC中,PF12+PF22=20.又PF1·PF2=2,∴(PF1-PF2)2=16,∴a2=4,∴b2=1.∴方程为-y2=1.故选D.3.(2019-2020福州一中学段模考)已知双曲线-=1的左、右焦点分别为F1,F2,P为双曲线右支上一点,且PF2的中点M在以O为圆心OF1为半径的圆上,则PF2=(C)A.12B.9C.4D.2[解析]如图,连接F1M、F1P,由圆的性质可得F1M⊥F2P,又M为PF2的中点,所以F1P=F1F2=2=12,则PF2=F1P-8=4.故选C.4.(2020·浙江湖州期末调研)双曲线C:-y2=1的左右焦点分别为F1,F2,P是双曲线右支上一点,则PF1-PF2=__2__.5.根据下列条件,求双曲线的标准方程:(1)c=,经过点(-5,2),且焦点在x轴上;(2)已知双曲线两个焦点的坐标为F1(0,-5),F2(0,5),双曲线上一点P到F1,F2的距离之差的绝对值等于6.[解析](1)因为c=,且焦点在x轴上,故可设标准方程为-=1(a2<6).因为双曲线经过点(-5,2),所以-=1,解得a2=5或a2=30(舍去).所以所求双曲线的标准方程为-y2=1.(2)因为双曲线的焦点在y轴上,所以设它的标准方程为-=1(a>0,b>0).因为2a=6,2c=10,所以a=3,c=5.所以b2=52-32=16.所以所求双曲线标准方程为-=1.课时作业·练素能A级基础巩固一、选择题1.双曲线-=1的焦距是(C)A.16B.4C.8D.22.在方程mx2-my2=n中,若mn<0,则方程的曲线是(D)A.焦点在x轴上的椭圆B.焦点在x轴上的双曲线C.焦点在y轴上的椭圆D.焦点在y轴上的双曲线[解析]方程mx2-my2=n可化为:-=1,∵mn<0,∴->0,∴方程的曲线是焦点在y轴上的双曲线.3.(2019-2020学年房山区期末检测)已知双曲线-=1的焦点为F1,F2,P为其上一点.若点P到F1的距离为15,则点P到F2的距离是(A)A.31B.1C.-1D.-1或31[解析]双曲线-=1的焦点为F1,F2,P为其上一点.所以PF1-PF2=2a=16,若点P到F1的距离为PF1=15,∴15-PF2=16,解得PF2=31或PF2=-1(舍去),所以点P到F2的距离是31.故选A.4.若k∈R,方程+=1表示焦点在x轴上的双曲线,则k的取值范围是(C)A.k<-3B.k>-2C.-3-2[思路分析]由于方程表示焦点在x轴上的双曲线,故k+3>0,k+2<0.[解析]由题意可知,,解得-30,b>0),且c=3,a2+b2=9.由条件知,双曲线与椭圆有一个交点的纵坐标为4,可得两交点的坐标为A(,4)、B(-,4),由点A在双曲线上知,-=1.解方程组,得.∴所求曲线的方程为-=1.三、解答题9.已知双曲线经过两点M(1,1)、N(-2,5),求双曲线的标准方程.[解析]设所求双曲线的标准方程为mx2+ny2=1(mn<0),将点M(1,1)、N(-2,5)代入上述方程,得到,解得.所以所求双曲线的标准方程为-=1.10.如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:x2+y2-10x+9=0,动圆M与定圆F1、F2都外切,求动圆圆心M的轨迹方程.[解析]圆F1:(x+5)2+y2=1,∴圆心F1(-5,0),半径r1=1.圆F2:(x-5)2+y2=42,∴圆心F2(5,0),半径r2=4.设动圆M的半径为R,则有MF1=R+1,MF2=R+4,∴MF2-MF1=33m2-2>0,解得-m>,则当x∈∪时,曲线是焦点在x轴上的椭圆,A正确;若3m2-2>m2+2,解得m<-或m>,此时曲线是焦点在y轴上的椭圆,B正确;若3m2-2<0,解得-PF2,由双曲线的定义知PF1-PF2=2,∴PF1=8,PF2=6,又c2=a2+b2=1+24=25,∴c=5,∴F1F2=10,∴△PF1F2为直角三角形S△PF1F2=PF1PF2=24.6.双曲线-=1的一个焦点到中心的距离为3,若焦点在x轴上,那么m=__7__,若焦点在y轴上,那么m=__-2__.[解析]当焦点在x轴上时,有m>5,则c2=m+m-5=9,∴m=7;当焦点在y轴上时,有m<0,则c2=-m+5-m=9,∴m=-2.三、解答题7.已知双曲线的焦点在坐标轴上,且一个焦点在直线5x-2y+20=0上,两焦点关于原点对称,且=,求双曲线的方程.[解析]易得直线5x-2y+20=0与两坐标轴交点为(-4,0)和(0,10).若(-4,0)为焦点,则c=4,而=,所以a=,b2=16-=.故双曲线的方程为-=1.若(0,10)为焦点,则c=10,故a=6,b2=100-36=64.故双曲线的方程为-=1.综上,双曲线的方程为-=1或-=1.8.在△ABC中,A、B、C所对三边分别为a、b、c,B(-1,0)、C(1,0),求满足sinC-sinB=sinA时顶点A的轨迹,并画出图形.[解析]∵sinC-sinB=sinA,∴c-b=a=×2=1,即AB-AC=1b就是AB>AC,可知A点的轨迹是双曲线的右支,还需除去点如图所示.',)


 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载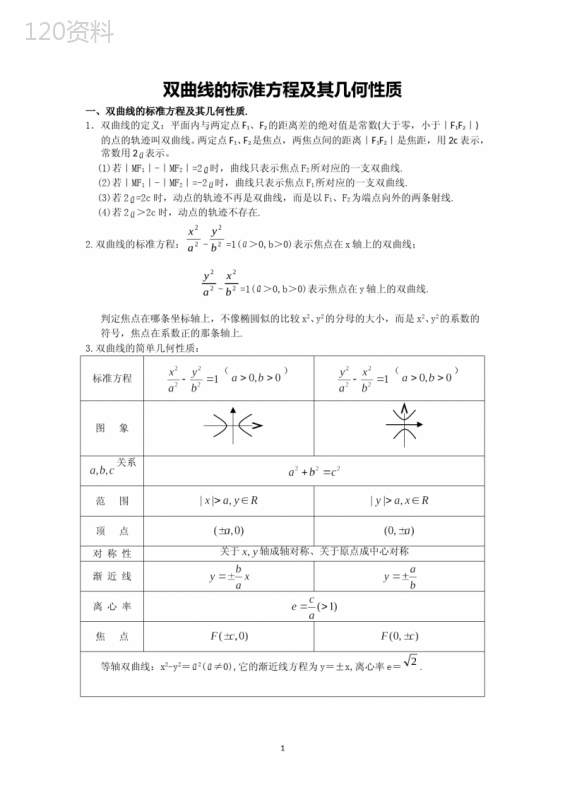 下载
下载 下载
下载