《抛物线及其标准方程》人教版高中数学选修2-1PPT课件（第2.4.1课时）.pptx

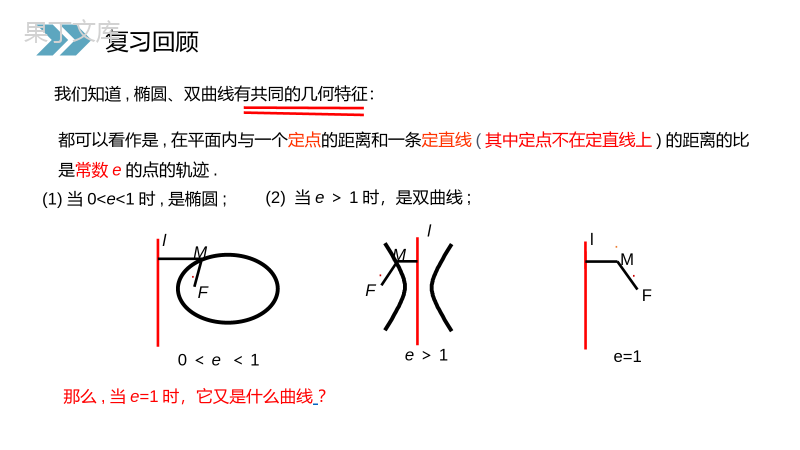
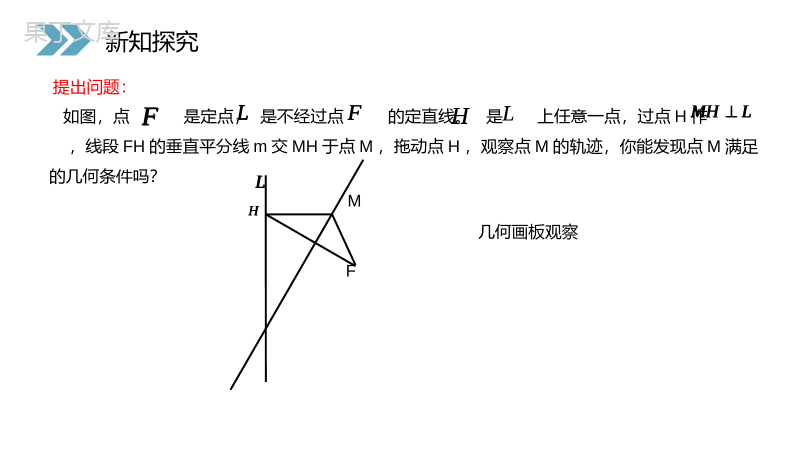
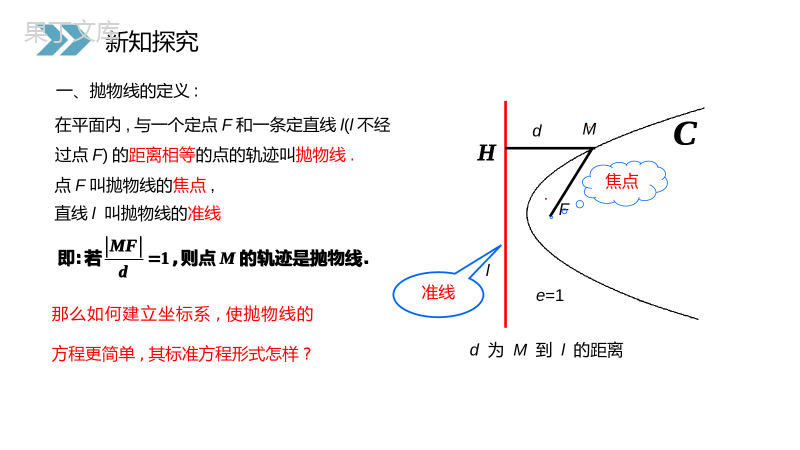
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-12.4.1抛物线及其标准方程第2章圆锥曲线与方程人教版高中数学选修2-1我们知道，二次函数y=ax2+bx+c（a≠0）的图象是一条抛物线，而且还研究过它的顶点坐标、对称轴等问题。那么，抛物线到底有怎样的几何特征？它还有哪些几何性质？思考：课前导入我们知道,椭圆、双曲线有共同的几何特征：都可以看作是,在平面内与一个定点的距离和一条定直线(其中定点不在定直线上)的距离的比是常数e的点的轨迹.·MFl0＜e＜1(2)当e＞1时，是双曲线;(1)当00)x2=2py(p>0)准线方程焦点坐标标准方程图形xFOylxFOylxFOylxFOyly2=2px(p>0))0,2p(2px)0,2p(2px)2p0(，2pyx2=-2py(p>0))2p0(，2py四．四种抛物线的对比新知探究)0,2p(2px)0,2p(2px)2p0(，2py)2p0(，2py思考：二次函数的图象为什么是抛物线？2(0)yaxa221(0)yaxaxya110)44aa焦点（，准线y=-当a>0时与当a<0时，结论都为：12pa新知探究yxoy=ax2+bx+cy=ax2+cy=ax22(0)yaxa221(0)yaxaxya110)44aa焦点（，准线y=-12pa例1（1）已知抛物线的标准方程是y2=6x，求它的焦点坐标及准线方程（2）已知抛物线的焦点坐标是F（0，－2），求抛物线的标准方程（3）已知抛物线的准线方程为x=1，求抛物线的标准方程（4）求过点A（3，2）的抛物线的标准方程焦点F(,0)32准线：x=－32x2=－8yy2=－4xy2=xx2=y4392新知探究1、根据下列条件，写出抛物线的标准方程：（1）焦点是F（3，0）；（2）准线方程是x=；14（3）焦点到准线的距离是2。y2=12xy2=xy2=4x、y2=-4x、x2=4y或x2=-4y2、求下列抛物线的焦点坐标和准线方程：(1)y2=20x(2)x2=y(3)2y2+5x=0(4)x2+8y=012焦点坐标准线方程(1)(2)(3)(4)（5，0）x=-5（0，—）18y=-—188x=—5（-—，0）58（0，-2）y=2课堂练习1412例2：一种卫星接收天线的轴截面如下图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接收天线，经反射聚集到焦点处。已知接收天线的径口（直径）为4.8m，深度为0.5m。建立适当的坐标系，求抛物线的标准方程和焦点坐标。yxBFAo.课堂练习yxBFAo.例3：点M与点F（4,0）的距离比它到直线l:x+5=0的距离小1，求点M的轨迹方程。yxFo.x=-5x=-4.MHG(4,0)题型二：利用抛物线的定义求点的轨迹方程课堂练习yxFo..例4：已知抛物线y2=2x的焦点是F，点P是抛物线上的动点，又有点A（3，2），求PA+PF的最小值，并求出取最小值时P点的坐标yxFo..PA(3,2).题型三：抛物线应用于求最值问题课堂练习yxFo...感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明y2=-2px(p>0)x2=2py(p>0)准线方程焦点坐标标准方程图形xFOylxFOylxFOylxFOyly2=2px(p>0))0,2p(2px)0,2p(2px)2p0(，2pyx2=-2py(p>0))2p0(，2py四种抛物线的对比)0,2p(2px)0,2p(2px)2p0(，2py)2p0(，2py讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-1感谢你的聆听第2章圆锥曲线与方程人教版高中数学选修2-1