参数方程下的曲率公式,参数方程下的曲率公式证明
本作品内容为参数方程下的曲率公式,格式为 doc ,大小 13410 KB ,页数为 3页

('参数方程下的曲率公式曲率的定义是物体的曲度,即当物体在特定的参数方程中,其表面自变量的变化程度。曲率公式是求取曲率的重要工具,它可以帮助我们计算物体表面的曲度,也可以用于曲面的平面展开,以及几何学中的微分几何。在几何学中,曲率是一个重要的度量,用它可以衡量曲面、曲线在不同空间上的弯曲程度。它有助于研究曲面、曲线在空间中的特性和轨迹,也可以应用于其他科学研究中。在参数方程下,可以计算出曲率的一个公式,即曲率公式。曲率公式可以表示为:κ=R(1+h^2)^(3/2)其中,R是曲率半径,h是曲面中自变量的变化率。曲率公式的求取基础是参数方程,参数方程是由物体表面的参数方程求取的,因此,了解参数方程是非常重要的。参数方程有三类:抛物面参数方程、凸反平面参数方程和椭圆回形参数方程。抛物面参数方程可以表示为:X=A+Ucosθ+VsinθY=B+U2sin2θ+V2cos2θZ=C+U2sin2θ+V2cos2θ其中,A,B,C是物体表面的常数参数,U,V是物体表面的自变量,θ是变量θ的参数值。1凸反平面参数方程可以表示为:X=A+Ucosθ+VsinθY=B+U2sin2θ+V2cos2θZ=C+V2cos2θU2sin2θ它和抛物面参数方程的区别是负号的使用。椭圆回形参数方程可以表示为:X=A+Ucosθ+VsinθY=B+U2sin2θ+V2cos2θZ=C+U2cos2θ+V2sin2θ它与抛物面参数方程的区别在于自变量的变化率是相反的。这三类参数方程可以用来求取曲率公式。我们可以准备三类参数之后,将物体表面的自变量U、V和参数θ代入曲率公式,就可以计算出物体表面的曲率值了。由于曲率公式可以用来测量物体表面的曲度,因此,在工程中有着广泛的应用。例如,它可以应用于构件的强度评估,也可以用于测量地形和气象环境的精细变化;它可以用于太阳能电池板的制造,也可以用于油藏的勘察中。此外,曲率公式还可以用于平面展开。平面展开是将曲面绘制成平面图形的过程,曲率公式可以用来测量曲面在特定自变量上的弯曲程度,从而帮助进行平面展开,这对于制作地图、印刷图片等等有着很大的帮助。以上就是参数方程下的曲率公式的基本内容。不同的参数方程2可以用来求取曲率公式,曲率公式可以用来帮助我们计算曲面的曲度,并可应用于工程中、图像平面展开等等。它不仅是一个简单的数学概念,也可以帮助我们更好地理解物体表面的曲度,从而使我们在实际应用中更好地发挥曲率公式的功效。3',)
提供参数方程下的曲率公式,参数方程下的曲率公式证明会员下载,编号:1700752445,格式为 docx,文件大小为3页,请使用软件:wps,office word 进行编辑,PPT模板中文字,图片,动画效果均可修改,PPT模板下载后图片无水印,更多精品PPT素材下载尽在某某PPT网。所有作品均是用户自行上传分享并拥有版权或使用权,仅供网友学习交流,未经上传用户书面授权,请勿作他用。若您的权利被侵害,请联系963098962@qq.com进行删除处理。

 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载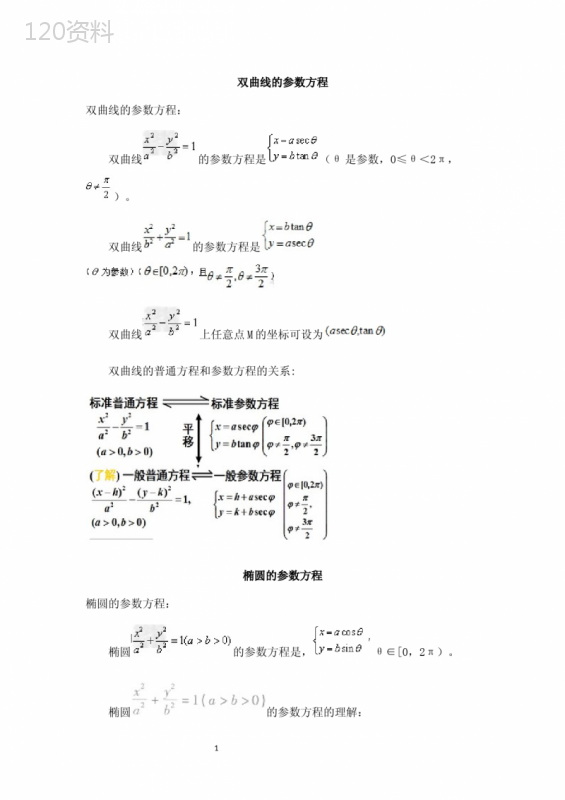 下载
下载 下载
下载