2022年云南省昆明市官渡区中考一模考试-数学-试题(学生版+解析版)

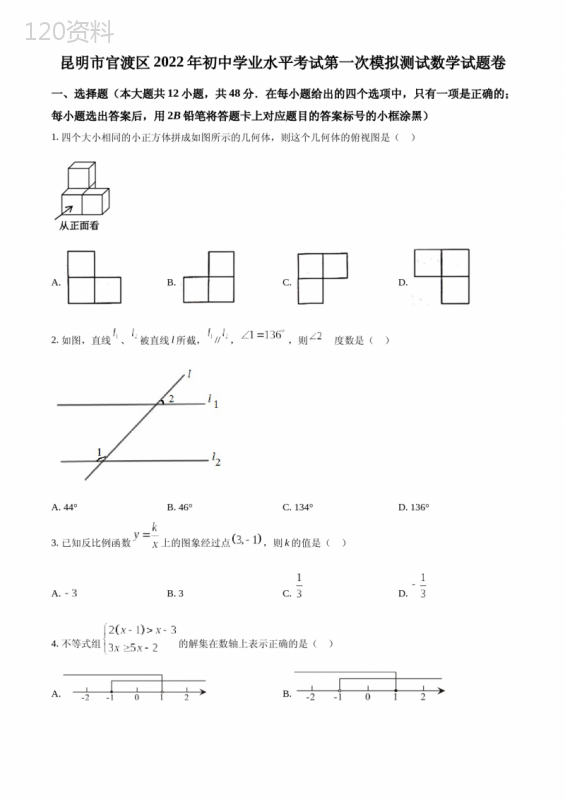
('昆明市官渡区2022年初中学业水平考试第一次模拟测试数学试题卷一、选择题（本大题共12小题，共48分．在每小题给出的四个选项中，只有一项是正确的；每小题选出答案后，用2B铅笔将答题卡上对应题目的答案标号的小框涂黑）1.四个大小相同的小正方体拼成如图所示的几何体，则这个几何体的俯视图是（）A.B.C.D.2.如图，直线、被直线l所截，//，，则的度数是（）A.44°B.46°C.134°D.136°3.已知反比例函数上的图象经过点，则k的值是（）A.B.3C.D.4.不等式组的解集在数轴上表示正确的是（）A.B.C.D.5.下列计算正确的是（）A.B.C.D.6.如图，，，是五边形的3个外角，若，则等于（）A.130°B.180°C.230°D.330°7.关于x的一元二次方程有实数根，则k的取值范围是（）A.B.且C.D.且8.如图，小明在数学兴趣小组探究活动中要测量河的宽度，他和同学在河对岸选定一点A，再在河的这一边选定点P和点B，使．利用工具测得米，，根据测量数据可计算得到小河宽度为（）A.米B.米C.米D.米9.按一定规律排列的单项式：a，，，，，，…，第2022个单项式是（）A.B.C.D.10.当今，大数据、云计算、人工智能等互联网新技术正在全方位改写中国社会，而应用将是推动互联网这个“最大变量”变成“最大增量”的新引擎，的出现将改变中国的经济格局，据预测，2020年到2030年中国直接经济产出和间接经济产出的情况如图所示，根据图提供的信息，下列推断不合理的是（）A.2022年间接经济产出比直接经济产出多2万亿元B.2026年直接经济产出为2021年直接经济产出的4倍C.2020年到2030年，直接经济产出和间接经济产出都是逐年增长D.2023年到2024年与2028年到2029年间接经济产出的增长率相同11.古希腊时期，人们认为最美人体的肚脐至脚底的长度与身高长度之比约为0.618，著名的“断臂维纳斯”便是如此．若王老师身高，肚脐到脚底的长度为，为使王老师穿上高跟鞋以后更接近最美人体比例，选择高跟鞋的跟高约为（）A.B.C.D.12.在平行四边形中，，，，点E是边上的动点，过点B作直线的垂线，垂足为F，当点E从点A运动到点B时，点F的运动路径长为（）A.B.C.D.2二、填空题（每小题4分，满分24分．请考生用黑色碳素笔将答案写在答题卡相应题号后的横线上）13.若二次根式在实数范围内有意义，则x的取值范围是______．14.若，则______．15.计算：______．16.如图，为的外接圆的直径，若，则的度数为______°．17.如图，正六边形的边长为4，以A为圆心，的长为半径画弧，得，连接，，则图中阴影部分的面积为______．18.已知二次函数，当时有最小值5，则a的值为______．三、解答题（共6小题，满分48分．请考生用黑色碳素笔在答题卡相应的题号后答题区域内作答，必须写出运算步骤、推理过程或文字说明，超出答题区域的作答无效.特别注意：作图时，必须使用黑色碳素笔在答题卡上作图）19.为培养学生良好的运动习惯，提高学生的身体素质，我校开展了“花样跳绳”和“春季长跑”等体育活动.体育老师随机抽取了八年级男、女各60名学生的长跑成绩，并将数据进行整理分析，给出了下面部分信息：数据分为A，B，C，D四个等级，分别是：A：，B：，C：，D：60名男生成绩的条形统计图以及60名女生成绩的扇形统计图如图：男生成绩位于B等级前10名的分数为：95，95，95，94，94，94，92，91，90，90.60名男生和60名女生成绩的平均数，中位数，众数如下表：性别平均数中位数众数男生94a96女生959496根据以上信息，解答下列问题：（1）填空：______，______；（2）计算抽取的男生成绩在B等级的人数，并补全条形统计图；（3）根据以上数据，你认为在此次活动中，男生成绩好还是女生成绩好？请说明理由（说明一条理由即可）．（4）若该年级有800名学生，估计成绩为A等级的学生约为______人．21.如图，有4张背面相同的纸牌A，B，C，D正面分别写着四个不同的数字．（1）求摸出一张纸牌恰好是负数的概率是______；（2）将这4张纸牌背面朝上洗匀后摸出一张，不放回，然后再摸出一张．求摸出两张牌面数字恰好一个是有理数，一个是无理数的概率．（用树状图或列表法求解，纸牌可用A，B，C，D表示）23.学习函数时，我们经历了“确定函数解析式、画出函数图象、利用函数图象研究函数性质、利用函数性质解决问题”的学习过程．以下是我们研究函数的图象和性质的部分过程，请按要求完成下列问题．（1）列表：y与x的部分对应值如下表，则______，______；x…0123…y…m0121n…（2）描点、连线：根据上表中的数据，在平面直角坐标系中画出函数的图象；（3）结合图象，写一条函数的性质：________________；（4）根据函数图象填空：①方程有______个解；②若关于x的方程无解，则a的取值范围是______．25.如图，是四边形的外接圆，是的直径，，交的延长线于点E，平分．\\（1）求证：是的切线；（2）若，，求的长．27.2022年北京冬奥会即将召开，激起了人们对冰雪运动的极大热情．如图是某跳台滑雪训练场的横截面示意图，取某一位置的水平线为轴，过跳台终点作水平线的垂线为轴，建立平面直角坐标系．图中的抛物线近似表示滑雪场地上的一座小山坡，某运动员从点正上方米处的点滑出，滑出后沿一段抛物线运动．（1）当运动员运动到离处的水平距离为米时，离水平线的高度为米，求抛物线的函数解析式（不要求写出自变量的取值范围）；（2）在（1）的条件下，当运动员运动水平线的水平距离为多少米时，运动员与小山坡的竖直距离为米？（3）当运动员运动到坡顶正上方，且与坡顶距离超过米时，求的取值范围．28.矩形中，、交于点O，（k为常数）．作，、分别与、边相交于点E、F，连接，（1）发现问题：如图1，若，猜想：______；（2）类比探究：如图2，，探究线段，之间的数量关系，并说明理由；（3）拓展运用：如图3，在（2）的条件下，若，，，求的长．昆明市官渡区2022年初中学业水平考试第一次模拟测试数学试题卷一、选择题（本大题共12小题，共48分．在每小题给出的四个选项中，只有一项是正确的；每小题选出答案后，用2B铅笔将答题卡上对应题目的答案标号的小框涂黑）1.四个大小相同的小正方体拼成如图所示的几何体，则这个几何体的俯视图是（）A.B.C.D.【1题答案】【答案】A【解析】【分析】根据从上面看所得到的图形是俯视图，可得答案．【详解】解：从上面看：第一层是一个小正方形，第二层是两个小正方形，左对齐．故选：A．【点睛】本题考查简单组合体的三视图．从上面看组合体，得到的图形是俯视图．2.如图，直线、被直线l所截，//，，则的度数是（）A.44°B.46°C.134°D.136°【2题答案】【答案】A【解析】【分析】由平行线的性质可得结果．【详解】解：因为l1//l2，∠1=136°，所以∠2的对顶角与∠1的和是180°，∴∠2=180°-136°=44°，故选A．【点睛】本题考查平行线的性质，找准角的关系是解题的关键．3.已知反比例函数上的图象经过点，则k的值是（）A.B.3C.D.【3题答案】【答案】A【解析】【分析】直接将点代入反比例函数中，即可求解．【详解】将点代入反比例函数，可得解得故选：A．【点睛】本题考查待定系数法求反比例函数解析式，准确计算是解题的关键．4.不等式组的解集在数轴上表示正确的是（）A.B.C.D.【4题答案】【答案】B【解析】【分析】分别解两个不等式，将解集在数轴上表示出来即可．【详解】解：解不等式①得，x>-1解不等式②得，x≤1所以不等式组的解集在数轴上表示为选项B中的图，故选B【点睛】本题考查解不等式组以及在数轴上表示不等式组的解集，正确掌握解集的表示方法是解题的关键．5.下列计算正确的是（）A.B.C.D.【5题答案】【答案】D【解析】【分析】根据合并同类项、积的乘方、单项式乘以多项式及异分母分式相加减计算，分别判断即可．【详解】A.，不能合并，错误，不符合题意；B.，错误，不符合题意；C.，错误，不符合题意；D.，正确，符合题意；故选：D．【点睛】本题考查了合并同类项、积的乘方、单项式乘以多项式及异分母分式相加减，熟练掌握运算法则是解题的关键．6.如图，，，是五边形的3个外角，若，则等于（）A.130°B.180°C.230°D.330°【6题答案】【答案】C【解析】【分析】根据多边形的外角和为360°，以及已知条件，求得，即可求得答案．【详解】如图，，，故选C【点睛】本题考查了多边形的外角和，掌握多边形的外角和是360度是解题的关键．7.关于x的一元二次方程有实数根，则k的取值范围是（）A.B.且C.D.且【7题答案】【答案】D【解析】【分析】根据一元二次方程根的判别式及其定义即可得结果．【详解】解：由题意可得k≠0，=，解得，故选D．【点睛】本题考查一元二次方程的定义及根的判别式，二次项系数不为零是容易忽略的地方，需注意．8.如图，小明在数学兴趣小组探究活动中要测量河的宽度，他和同学在河对岸选定一点A，再在河的这一边选定点P和点B，使．利用工具测得米，，根据测量数据可计算得到小河宽度为（）A.米B.米C.米D.米【8题答案】【答案】C【解析】【分析】根据正切定义，把公式变形得到结果．【详解】解：∵，∴．故选C．【点睛】本题考查了正切的定义，熟练掌握正切定义是解决本题的关键．9.按一定规律排列的单项式：a，，，，，，…，第2022个单项式是（）A.B.C.D.【9题答案】【答案】B【解析】【分析】系数的规律：第n个对应的系数是2n﹣1，且奇数项为正，偶数项为负，指数的规律：第n个对应的指数是n，由此求解即可．【详解】解：根据分析的规律，得系数的规律：第n个对应的系数是2n﹣1，且奇数项为正，偶数项为负，指数的规律：第n个对应的指数是n，第2022个单项式是-4043x2022，故B正确．故选：B．【点睛】本题主要考查了单项式问题，分别找出单项式的系数和次数的规律是解决此类问题的关键．10.当今，大数据、云计算、人工智能等互联网新技术正在全方位改写中国社会，而应用将是推动互联网这个“最大变量”变成“最大增量”的新引擎，的出现将改变中国的经济格局，据预测，2020年到2030年中国直接经济产出和间接经济产出的情况如图所示，根据图提供的信息，下列推断不合理的是（）A.2022年间接经济产出比直接经济产出多2万亿元B.2026年直接经济产出为2021年直接经济产出的4倍C.2020年到2030年，直接经济产出和间接经济产出都是逐年增长D.2023年到2024年与2028年到2029年间接经济产出的增长率相同【10题答案】【答案】D【解析】【分析】折线图是用一个单位表示一定的数量，根据数量的多少描出各点，然后把各点用线段依次连接起来．以折线的上升或下降来表示统计数量增减变化．【详解】解：根据折线统计图，可知：A.2022年5G间接经济产出比5G直接经济产出多：4-2=2（万亿），故此项不合题意；B.4÷1=4(倍)，故2026年直接经济产出为2021年直接经济产出的4倍，故此项不合题意；C.2020年到2030年，5G直接经济产出和5G间接经济产出都是逐年增长，故此项不合题意；D.2023年到2024年5G间接经济产出的增长率为：（6-5）÷5=20%，2028年到2029年5G间接经济产出的增长率为：（9-8）÷8=12.5%，故2023年到2024年与2028年到2029年5G间接经济产出的增长率不相同，故此项符合题意；故选：D【点睛】本题考查了折线统计图，熟练读懂折线统计图是解题思的关键．11.古希腊时期，人们认为最美人体的肚脐至脚底的长度与身高长度之比约为0.618，著名的“断臂维纳斯”便是如此．若王老师身高，肚脐到脚底的长度为，为使王老师穿上高跟鞋以后更接近最美人体比例，选择高跟鞋的跟高约为（）A.B.C.D.【11题答案】【答案】B【解析】【分析】设选择高跟鞋的跟高约为x厘米，根据“最美人体的肚脐至脚底的长度与身高长度之比约为0.618”列方程，求解即可．【详解】设选择高跟鞋的跟高约为x厘米，由题意得解得所以，选择高跟鞋的跟高约为5厘米．故选：B．【点睛】本题考查了分式方程的实际应用，能够根据题意列出分式方程是解题的关键．12.在平行四边形中，，，，点E是边上的动点，过点B作直线的垂线，垂足为F，当点E从点A运动到点B时，点F的运动路径长为（）A.B.C.D.2【12题答案】【答案】B【解析】【分析】根据∠BFC=90°，判定点F在以BC为直径的圆上的一段弧上运动，设BD与AC的交点为G，则点F的路径长恰好是，求得半径和圆心角计算即可．【详解】如图，连接AC，BD，二线交于点G，∵平行四边形中，，，∴四边形ABCD是菱形，∴BG⊥AC,∴点G在以BC为直径的圆上，设圆心为O，则半径OB=，连接OG，∵，∴∠ABC=60°，∴△ABC是等边三角形∴∠ACB=60°，∴△GOC是等边三角形，∴∠GOC=60°，∠GOB=120°，根据题意，点F的运用路径为，∴的长为：，故选B．【点睛】本题考查了菱形的判定和性质，等边三角形的判定和性质，圆的基本性质，弧长公式，熟练掌握圆的基本性质，灵活运用弧长公式计算是解题的关键．二、填空题（每小题4分，满分24分．请考生用黑色碳素笔将答案写在答题卡相应题号后的横线上）13.若二次根式在实数范围内有意义，则x的取值范围是______．【13题答案】【答案】【解析】【分析】根据二次根式有意义的条件进行求解即可．【详解】二次根式在实数范围内有意义解得故答案为：．【点睛】本题考查了二次根式有意义的条件，即被开方数大于等于0，熟练掌握知识点是解题的关键．14.若，则______．【14题答案】【答案】1【解析】【分析】先根据完全平方公式变形，再由绝对值和偶次方的非负性得到a、b的值，代入计算即可．【详解】由题意得，且故答案为：1．【点睛】本题考查了整式的化简求值，涉及完全平方公式、绝对值的性质、偶次方的非负性质，熟练掌握知识点是解题的关键．15.计算：______．【15题答案】【答案】-4【解析】【分析】先算零次幂、负整数指数幂以及乘方，再算加减，即可得到答案．【详解】故答案为：-4．【点睛】本题考查了有理数的混合运算，涉及零次幂、负整数指数幂以及乘方，熟练掌握运算法则是解题的关键．16.如图，为的外接圆的直径，若，则的度数为______°．【16题答案】【答案】35【解析】【分析】由直径所对的圆周角是90°和同弧所对的圆周角相等可得结果．【详解】解：如图，连接BC，∵AB是直径，∴∠ACD+∠BCD=90°，又∵∠BCD=∠BAD=55°，∴∠ACD=90°-55°=35°．故答案为35【点睛】本题考查了圆周角定理的推论，直径所对圆周角性质，找到等角进行代换是解题的关键．17.如图，正六边形的边长为4，以A为圆心，的长为半径画弧，得，连接，，则图中阴影部分的面积为______．【17题答案】【答案】【解析】【分析】由正六边形ABCDEF的边长为4，可得AB=BC=4，∠ABC=∠BAF=120°，进而求出∠BAC=30°，∠CAE=60°，过B作BH⊥AC于H，由等腰三角形的性质和含30°直角三角形的性质得到AH=CH，BH=2．在Rt△ABH中，由勾股定理求得AH=，得到．最后根据扇形的面积公式即可得到阴影部分的面积．【详解】解：∵正六边形ABCDEF的边长为4，∴AB=BC=4，，∵∠ABC+∠BAC+∠BCA=180°，∴，如图，过B作BH⊥AC于H，∴AH=CH，，在Rt△ABH中，，∴．同理可求∠EAF=30°，∴，∴∴图中阴影部分的面积为8π，故答案为：8π．【点睛】本题考查的是正六边形的性质和扇形面积的计算、等腰三角形的性质、勾股定理，掌握扇形面积公式是解题的关键．18.已知二次函数，当时有最小值5，则a的值为______．【18题答案】【答案】或4【解析】【分析】把二次函数配成顶点式，分三种情况进行讨论：当对称轴在所给范围内，和对称轴在所给范围的左侧，右侧，即可求得答案．【详解】解：，当时，最小值为1，与题意不符；当时，二次函数在1≤x≤2上y随x的增大而增大，最小值为当x=1时，即（1-a）2+1=5，解得a=-1，或a=3（舍去）；当a≥2时，二次函数在1≤x≤2上y随x的增大而减小，最小值为当x=2时，即（2-a）2+1=5，解得a=4，或a=0（舍去）；所以a的值为-1或4．故答案为-1或4．【点睛】本题考查二次函数的最值问题，因对称轴的位置未知，故根据题意分情况讨论是解题的关键．三、解答题（共6小题，满分48分．请考生用黑色碳素笔在答题卡相应的题号后答题区域内作答，必须写出运算步骤、推理过程或文字说明，超出答题区域的作答无效.特别注意：作图时，必须使用黑色碳素笔在答题卡上作图）19.为培养学生良好的运动习惯，提高学生的身体素质，我校开展了“花样跳绳”和“春季长跑”等体育活动.体育老师随机抽取了八年级男、女各60名学生的长跑成绩，并将数据进行整理分析，给出了下面部分信息：数据分为A，B，C，D四个等级，分别是：A：，B：，C：，D：60名男生成绩的条形统计图以及60名女生成绩的扇形统计图如图：男生成绩位于B等级前10名的分数为：95，95，95，94，94，94，92，91，90，90.60名男生和60名女生成绩的平均数，中位数，众数如下表：性别平均数中位数众数男生94a96女生959496根据以上信息，解答下列问题：（1）填空：______，______；（2）计算抽取的男生成绩在B等级的人数，并补全条形统计图；（3）根据以上数据，你认为在此次活动中，男生成绩好还是女生成绩好？请说明理由（说明一条理由即可）．（4）若该年级有800名学生，估计成绩为A等级的学生约为______人．【19题答案】【答案】（1）93，30（2）抽取的男生成绩在B等级的人数是16，补全条形统计图见解析（3）女生的成绩较好．理由见解析（4）320【解析】【分析】（1）先求解B等级的人数，再确定第第30个，第31个数据分别为：94分，92分，从而可得中位数，利用1减去女生A，C，D组的百分比可得答案；（2）由（1）可得B等级的人数，再补全统计图即可；（3）从平均数或中位数进行分析即可；（4）由该年级有800名学生，由800乘以成绩为A等级的百分比即可得到答案.【小问1详解】解：B等级的人数有（人），所以排序后排在第30个，第31个数据的平均数为中位数，而第30个，第31个数据分别为：94分，92分，所以平均数为：（分），【小问2详解】解：由（1）得：男生B组有16人，补全图形如下：【小问3详解】解：女生的成绩较好．理由：从平均数看，女生成绩平均数95大于男生成绩平均数94，说明女生平均成绩略高于男生；或从中位数看，女生成绩中位数94大于男生成绩中位数93，说明有一半女生成绩不低于94分，说明女生成绩好于男生.【小问4详解】解：（人）．所以该年级有800名学生，估计成绩为A等级的学生约为320人.【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用样本估计总体，利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．21.如图，有4张背面相同的纸牌A，B，C，D正面分别写着四个不同的数字．（1）求摸出一张纸牌恰好是负数的概率是______；（2）将这4张纸牌背面朝上洗匀后摸出一张，不放回，然后再摸出一张．求摸出两张牌面数字恰好一个是有理数，一个是无理数的概率．（用树状图或列表法求解，纸牌可用A，B，C，D表示）【21题答案】【答案】（1）（2）摸出两张牌面数字恰好一个是有理数，一个是无理数的概率为．【解析】【分析】（1）四张牌中，有两张背面是负数，根据随机事件的概率计算公式即可求解；（2）列表如图所示，然后根据概率公式计算求解即可．【小问1详解】解：随机摸出一张，共有四种结果，其中为负数的结果为两个∴摸出一张纸牌恰好是负数的概率是故答案为：．【小问2详解】解：列表如图所示，共有12种等可能结果其中摸出两张牌面数字恰好一个是有理数，一个是无理数的结果有6种，分别是（A，D）、（B，D）、（C，D）、（D，A）、（D，B）、（D，C）∴两张牌面数字恰好一个是有理数，一个是无理数的概率为．【点睛】本题考查随机事件的概率，用列举法求概率，明确题意做到不重不漏是关键．23.学习函数时，我们经历了“确定函数解析式、画出函数图象、利用函数图象研究函数性质、利用函数性质解决问题”的学习过程．以下是我们研究函数的图象和性质的部分过程，请按要求完成下列问题．（1）列表：y与x的部分对应值如下表，则______，______；x…0123…y…m0121n…（2）描点、连线：根据上表中的数据，在平面直角坐标系中画出函数的图象；（3）结合图象，写一条函数的性质：________________；（4）根据函数图象填空：①方程有______个解；②若关于x的方程无解，则a的取值范围是______．【23题答案】【答案】（1）-1，0（2）见解析（3）函数图象关于y轴对称；（其他答案合理即可）（4）①1；②．【解析】【分析】（1）将和分别代入，即可求出m和n的值；（2）根据描点法即可画出图象；（3）结合图象，写出其一条性质即可；（4）①结合图象，判断直线，与的图象的交点个数即可；②结合图象，判断直线，与的图象没有交点时的a的取值范围即可．【小问1详解】将代入，得，将代入，得，∴=-1，=0．故答案为：-1，0；【小问2详解】函数图象如下：【小问3详解】结合图象可知函数图象关于y轴对称，故答案为：函数图象关于y轴对称；（其他答案合理即可）【小问4详解】①根据图象可知直线，与的图象只有一个交点，∴方程有1个解；②若关于x的方程无解，则直线，与的图象没有交点，即即可．故答案为：1，．【点睛】本题考查一次函数的图象和性质，两直线的交点问题等知识．利用数形结合的思想是解题关键．25.如图，是四边形的外接圆，是的直径，，交的延长线于点E，平分．\\（1）求证：是的切线；（2）若，，求的长．【25题答案】【答案】（1）见解析（2）AD=【解析】【分析】（1）连接OB，求出OB∥DE，推出EB⊥OB，根据切线的判定得出即可；（2）根据HL证明Rt△ACB≌Rt△ACD，得∠ACB=∠ACD，AB=AD，求出∠CBE=30°，得BC=2CE=，AC=2BC=，在Rt△ACB中，由勾股定理得AB＝，从而可得结论【小问1详解】如图，连接OB，∵CB平分∠ACE．∴∠ACB＝∠ECB；∵OB＝OC，∴∠BCO＝∠CBO，∴∠BCE＝∠CBO，∴OB∥ED，∴∠E+∠EBO=180°；∵BE⊥ED，∴∠E=90°，∴∠EBO=180°-∠E=90°，∴EB⊥BO；∵OB是⊙O的半径，∴BE是⊙O的切线；【小问2详解】∵AC是⊙O的直径，∴∠ABC=∠ADC＝90°，∵在Rt△ACB和Rt△ACD中，∴Rt△ACB≌Rt△ACD（HL）∴∠ACB=∠ACD，AB=AD又∵∠ACB＝∠ECB；∠ECB+∠ACB+∠ACD＝180°，∴∠ECB=∠ACB=∠ACD＝60°∵∠E=90°，∴∠CBE=30°，∵CE＝，∴BC=2CE=；∵∠ABC=90°，∠ACB＝60°∴∠BAC=30°∴AC=2BC=∵在Rt△ACB中，由勾股定理得：AB＝∴AD=AB=【点睛】本题考查了切线的判定和性质，全等三角形的判定与性质以及勾股定理等知识，正确地作出辅助线是解题的关键．27.2022年北京冬奥会即将召开，激起了人们对冰雪运动的极大热情．如图是某跳台滑雪训练场的横截面示意图，取某一位置的水平线为轴，过跳台终点作水平线的垂线为轴，建立平面直角坐标系．图中的抛物线近似表示滑雪场地上的一座小山坡，某运动员从点正上方米处的点滑出，滑出后沿一段抛物线运动．（1）当运动员运动到离处的水平距离为米时，离水平线的高度为米，求抛物线的函数解析式（不要求写出自变量的取值范围）；（2）在（1）的条件下，当运动员运动水平线的水平距离为多少米时，运动员与小山坡的竖直距离为米？（3）当运动员运动到坡顶正上方，且与坡顶距离超过米时，求的取值范围．【27题答案】【答案】（1）；（2）12米；（3）．【解析】【分析】（1）根据题意可知：点A（0，4）点B（4，8），利用待定系数法代入抛物线即可求解；（2）高度差为1米可得可得方程，由此即可求解；（3）由抛物线可知坡顶坐标为，此时即当时，运动员运动到坡顶正上方，若与坡顶距离超过米，即，由此即可求出b的取值范围．【详解】解：（1）根据题意可知：点A（0，4），点B（4，8）代入抛物线得，，解得：，∴抛物线的函数解析式；（2）∵运动员与小山坡的竖直距离为米，∴，解得：（不合题意，舍去），，故当运动员运动水平线的水平距离为12米时，运动员与小山坡的竖直距离为米；（3）∵点A（0，4），∴抛物线，∵抛物线，∴坡顶坐标为，∵当运动员运动到坡顶正上方，且与坡顶距离超过米时，∴，解得：．【点睛】本题属二次函数应用中的难题.解决函数应用问题的一般步骤为：（1）审题：弄清题意，分清条件和结论，理清数量关系；(2)建模：将文字语言转化为数学语言，利用数学知识建立相应的数学模型；（3）求模：求解数学模型，得到数学结论；(4)还原：将用数学方法得到的结论还原为实际问题．28.矩形中，、交于点O，（k为常数）．作，、分别与、边相交于点E、F，连接，（1）发现问题：如图1，若，猜想：______；（2）类比探究：如图2，，探究线段，之间的数量关系，并说明理由；（3）拓展运用：如图3，在（2）的条件下，若，，，求的长．【28题答案】【答案】（1）1（2）当k≠1时，OE＝k•OF．理由见解析（3）【解析】【分析】（1）根据题意可知，此时四边形ABCD为正方形，然后证明△OEB≌△OFC，从而得出结论即可；（2）过O作OM⊥AB于点M，作ON⊥BC于点N，利用相似三角形的判定与性质证明即可；（3）过点O作OM⊥AB于点M，ON⊥BC于点N．由，BC＝k•ABAB，根据四边形ABCD是矩形，则∠ABC＝90°，跟据矩形的性质可知OA＝OC＝OD＝OB＝，则AB2+5AB2＝96，则可得AB＝，由此可知BC，CF＝OF，OB＝OC，进而可得角相等，由相等的角可证△COF∽△CBO，则，可得CF＝，则OF＝CF＝，因为OEOF，则可知OE＝，由勾股定理求解即可．【小问1详解】解：若k=1，则BC=AB，即四边形ABCD为正方形，∴OB=OC，∠OBE=∠OCF=45°，∠BOC=90°，∵∠EOF=∠BOC=90°，∴∠EOB=∠FOC，∴△OEB≌△OFC，∴OE=OF，∴，故答案为：1；【小问2详解】结论：当k≠1时，OE＝k•OF．理由：过点O作OM⊥AB于点M，ON⊥BC于点N．∴∠OME＝∠ONF＝∠ONB＝90°∵∠MBN＝90°∴四边形BMON是矩形∴∠MON＝∠EOF＝90°∴∠MON-∠EON=∠EOF-∠EON即∠MOE＝∠NOF又∵∠OME＝∠ONF∴△OME∽△ONF∴∵AO＝OC，OM∥BC∴AM＝MB∴OM=BC，同法可证ON=AB∴∴OE＝k•OF；【小问3详解】如图，过点O作OM⊥AB于点M，ON⊥BC于点N．∵，BC＝k•ABAB∵四边形ABCD是矩形∴∠ABC＝90°，OA＝OC＝OD＝OB＝∴AB2+5AB2＝96∴AB＝∴BC∵CF＝OF，OB＝OC∴∠FOC＝∠FCO＝∠OBC又∵∠OCF＝∠BCO∴△COF∽△CBO∴∴∴CF＝∴OF＝CF＝∵OEOF，∴OE＝，∴．【点睛】本题考查相似三角形的判定与性质，全等三角形的判定与性质，矩形的性质，勾股定理等，灵活根据题意构造相似三角形，熟练掌握相似三角形的性质是解题的关键．',)