19章1-第2课时-函数的图象

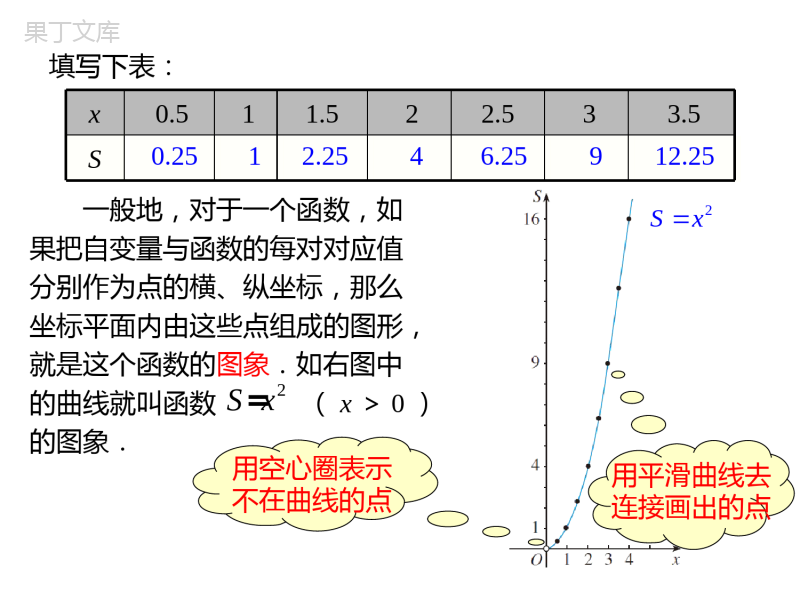
19.1.2函数的图象第十九章一次函数导入新课讲授新课当堂练习课堂小结八年级数学下（RJ）教学课件第1课时函数的图象情境引入学习目标1.理解函数的图象的概念；2.掌握画函数图象的一般步骤,能画出一些简单的函数图象；（重点）3.能根据所给函数图象读出一些有用的信息.（难点）导入新课在平面直角坐标系中，平面内的点可以用一对来表示.即坐标平面内的与有序数对是一一的.问题引入有序数对点对应思考：对于某个函数，给定一个自变量的值x，确定唯一的函数值y，由此能否确定一个点(x，y)呢?(a，b)ab讲授新课函数图象的意义一正方形面积S与边长x之间的函数解析式为S=x2．思考：（1）这个函数的自变量取值范围是什么？（2）怎样获得组成图形的点？先确定点的坐标问题：请画出下面问题中能直观地反映函数变化规律的图形：0x＞（4）自变量x的一个确定的值与它所对应的唯一的函数值S，是否唯一确定了一个点（x，S）呢？取一些自变量的值，计算出相应的函数值．（3）怎样确定满足函数关系的点的坐标？填写下表：x0.511.522.533.5S0.2512.2546.25912.25一般地，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象．如右图中的曲线就叫函数（x＞0）的图象．2=Sx2Sx用空心圈表示不在曲线的点用平滑曲线去连接画出的点-3O414248T/℃t/时思考：下图是自动测温仪记录的图象，它反映了北京的春季某天气温T如何随时间t的变化而变化．你从图象中得到了哪些信息？（1）从这个函数图象可知：这一天中气温最低（）,气温最高（）凌晨4时-3°C14时8°C（2）从___至气温呈下降状态，从4时至14时气温呈上升状态，从至气温又呈下降状态.（3）我们可以从图象中看出这一天中任一时刻的气温大约是多少.0时4时14时24时例1下图反映的过程是小明从家去食堂吃早餐，接着去图书馆读报，然后回家．其中x表示时间，y表示小明离家的距离，小明家、食堂、图书馆在同一直线上．825285868x/min0.80.6y/kmO根据图象回答下列问题：（1）食堂离小明家多远？小明从家到食堂用了多少时间？典例精析解：（1）食堂离小明家0.6km，小明从家到食堂用了8min.（2）小明在食堂吃早餐用了多少时间？825285868x/min0.80.6y/kmO（2）25-8=17，小明在食堂吃早餐用了17min.825285868x/min0.80.6y/kmO（3）食堂离图书馆多远？小明从食堂到图书馆用了多少时间？（3）0.8-0.6=0.2，食堂离图书馆0.2km；28-25=3，小明从食堂到图书馆用了3min.825285868x/min0.80.6y/kmO（4）小明读报用了多长时间？（4）58-28=30，小明读报用了30min.（5）图书馆离小明家多远？小明从图书馆回家的平均速度是多少？825285868x/min0.80.6y/kmO（5）图书馆离小明家0.8km，小明从图书馆回家用了68-58=10(min)，由此算出的平均速度是0.08km/min.画函数图象二问题：函数图象是坐标平面上以自变量的值为横坐标、以对应的函数值为纵坐标的点组成的曲线，函数图象直观地反映了变量之间的对应关系和变化规律．那么，怎样画一个函数的图象呢？例2在下列式子中，对于x的每一个确定的值，y都有唯一的对应值，即y是x的函数.画出这些函数的图象：（1）；（2）.解：（1）从函数解析式可以看出，x的取值范围是：第一步：从x的取值范围中选取一些简洁的数值，算出y的对应值，填写在表格里：xy621yxx…-3-2-10123…y……-5-3-11357全体实数Oxy12345-4-3-2-131425-2-4-1-3y=2x+1第二步：根据表中数值描点（x，y）；第三步：用平滑曲线连接这些点.当自变量的值越来越大时，对应的函数值.画出的图象是一条，直线越来越大-6x…-5-4-3-2-112345…y……6-3-2-1.2-1.5321.51.2为什么没有“0”？解：(2)列表：取一些自变量的值，并求出对应的函数值，填入表中.y5xO-4-3-2-112345-51234-1-2-3-4-56-6(2)描点：分别以表中对应的x、y为横纵坐标,在坐标系中描出对应的点.(3)连线：用光滑的曲线把这些点依次连接起来.(1,-6)第一步，列表——表中给出一些自变量的值及其；第二步，描点——在平面直角坐标系中，以自变量的值为，相应的函数值为，描出表格中数值对应的各点；第三步：连线——按照横坐标的顺序，把所描出的各点用连接起来.对应的函数值横坐标纵坐标平滑曲线由小到大归纳总结画函数图象的一般步骤：（1）画出函数的图象；列表：描点并连线：（2）从图象中观察，当x＜0时，y随x的增大而增大，还是y随x的增大而减小?当x＞0时呢？x-3-2-10123y94101492yx2yx当x＜0时，y随x的增大而减小；当x>0时，y随x的增大而增大.练一练我们知道，函数图象是以自变量的值和对应的函数值分别为横、纵坐标的点组成的图形，这样的点有无数个，那么怎样判断一个点是否在函数图象上？（1）判断下列各点是否在函数的图象上？①（-0.5，1）；②（1.5，4）．（2）判断下列各点是否在函数的图象上？①（2，3）；②（4，2）．6=yx21yx通常的方法是把点的横坐标（即自变量x）的取值代入解析式求出相应的函数值y值，看是否等于该点的纵坐标，如果等于，则该点在函数图象上；如不在，则该点不在函数图象上.1.在所给的平面直角坐标系中画出函数的图象.（先填写下表，再描点、连线）xy21x…-3-2-10123…y……当堂练习32-112012132Oxy12345-4-3-2-131425-2-4-1-3（1）体育场离张强家多远？张强从家到体育场用了多少时间？不在答：2.5千米.答：15分钟.2.点P（2，5）（填“在”或“不在”）函数y=2x的图象上.3.下面的图象反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家，图中x表示时间，y表示张强离家的距离.（2）体育场离文具店多远？（3）张强在文具店停留了多少时间？（4）张强从文具店回家的平均速度是多少？答：2.5-1.5=1（千米）答：65-45=20（分）1.5100656071.512187解：依题意可得（千米/时）课堂小结函数的图象图象的画法图象表达的实际意义描点列表连线