反比例函数(课件)-2022-2023学年九年级数学上册同步精品课堂(北师大版)

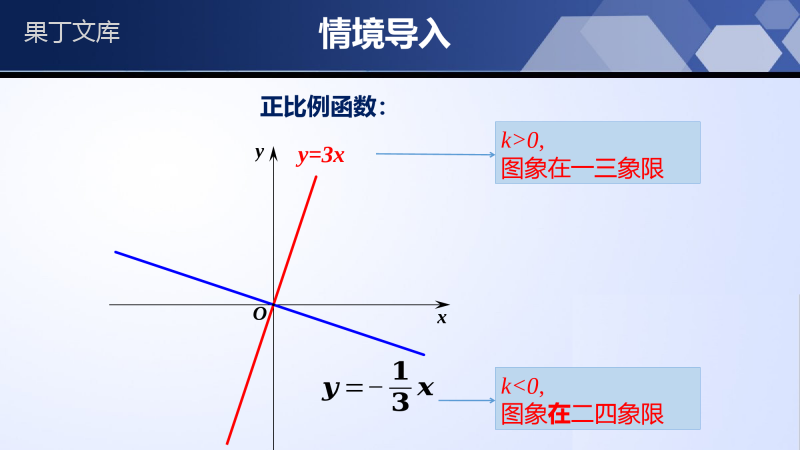
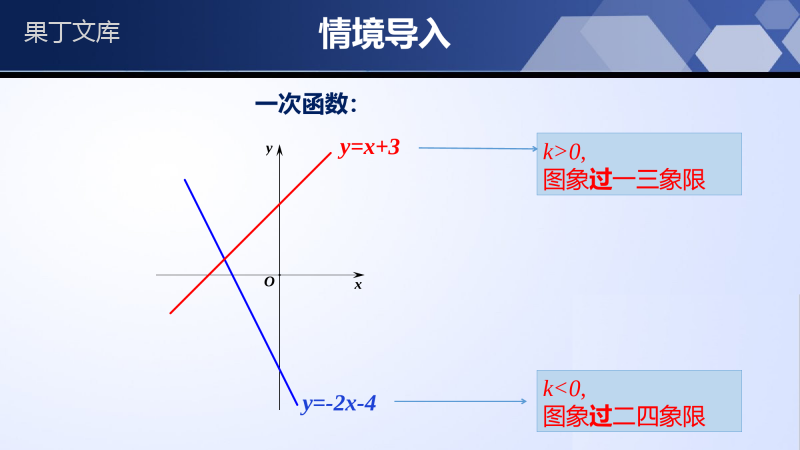
新课标北师大版九年级上册6.1反比例函数第六章反比例函数学习目标1、领会反比例函数的意义，理解并掌握反比例函数的概念，并能判断两个变量是否具有反比例函数关系。2、会判断一个函数是不是反比例函数。3、能结合具体问题确定反比例函数的表达式，并明确自变量的取值范围。情境导入)0(kkkxy为常数，)0,(kbkbkxy为常数，以前学过哪些函数？正比例函数：一次函数：)0(kkkxy为常数，)0,(kbkbkxy为常数，情境导入正比例函数：xyOy=3x?=−???k>0,图象在一三象限k<0,图象在二四象限情境导入k>0,图象过一三象限k<0,图象过二四象限一次函数：xyOy=-2x-4y=x+3情境导入生活是五彩缤纷的，在我们的数学世界里，虽然没有那么多美丽的色彩，但是却有许多美丽而神奇的线．它们充满了智慧，给我们展现了一个睿智的世界．瞧，旭日中学正在举行100米赛跑．你知道琳琳和华华两位同学的比赛成绩与他们的速度有什么样的函数关系吗?比赛用时越短，比赛成绩就越高.探究新知核心知识点一：反比例函数的定义我们知道，电流I、电阻R、电压U之间满足关系式U＝IR，当U＝220V时：（1）你能用含有R的代数式表示I吗？UIR（2）利用你写出的关系式完成下表：当R越来越大时，I是怎样变化的？当R越来越小呢？R/Ω20406080100I/A115.52.2113114UIR113114探究新知想一想：你能利用我们刚刚讨论的结论来解释“亮度可以调节的台灯”的原理吗？（3）变量I是R的函数吗？为什么？变量I是R的函数，I随着R的变化而变化.议一议：变量I是R的正比例函数吗？I是R的一次函数吗？I不是R的正比例函数，也不是R的一次函数，它不满足正比例函数和一次函数的形式.变量I是R的什么函数呢？UIRUIR探究新知京沪高速铁路全长约为1318km，列车沿京沪高速铁路从上海驶往北京，列车行完成全程所需的时间t（h）与行驶的平均速度v(km/h)之间有怎样的关系？变量t是v的函数吗？为什么？1318tv变量t是v的函数，t随着v的变化而变化.1318tv探究新知共同特点：（1）每个表达式都有3个量，其中两个变量，一个是不变量；（2）表达式右边是个分式形式，且分子上为常量，分母上为单项式，且单项式的次数为1；（3）这些式子都是函数.观察和,这些函数关系有什么共同的特点呢？1318tvUIR1318tvUIR探究新知观察和,这些函数有什么共同的特征吗？1318tvUIR一般地，如果两个变量x，y之间的关系可以表示成（k为常数，k≠0）的形式，那么称y是x的反比例函数.xky反比例函数的自变量x不能为零.1kxykxyxky反比例函数的三种形式(k≠0)1318tvUIRxky1kxykxyxky探究新知归纳总结注意：①常数k≠0；②自变量x不能为零（因为分母为0时，该式没意义）；③当写成时注意x的指数为﹣1.④由可得，所以两个变量的乘积即为k的xky1kxykxyxkyxky1kxykxyxky探究新知核心知识点二：用待定系数法求反比例函数y是x的反比例函数，下表给出了x与y的一些值。(1)写出这个反比例函数的表达式；(2)根据函数表达式完成上表；(3)自变量x能取哪些值？x-2-113y2-1-314-4-221212-2323-x≠0的所有实数。设：这个反比例函数的表达式为：y=kx将x=-1，y=2代入y=kx2=k-1解得：k=-2y=-2x探究新知设：用待定系数法确定反比例函数的表达式的步骤：写出反比例函数的表达式解方程求出该待定系数。把已知条件代入所设的表达式，设含有待定系数的反比例函数表达式。写：解：代：得到关于待定系数的方程。归纳总结探究新知例：若是关于x的反比例函数，32mx2my确定m的值。32mx2my解：∵是关于x的反比例函数∴m²-3=1且m+2≠0由m²-3=1得：m1=2，m2=-2，由m+2≠0得：m≠-2∴m=232mx2my32mx2my探究新知例例：已知y是x的反比例函数，当x＝2时，y＝6.(1)写出y与x的函数关系式；(2)求当x＝4时，y的值．解：(1)设y＝kx，因为x＝2时，y＝6，所以有6＝k2解得k＝12，因此y＝12x.(2)把x＝4代入y＝12x，得y＝124＝3.y＝kx，6＝k2y＝12x.y＝12x，得y＝124＝3.随堂练习1．已知函数y＝kx，当x＝1时，y＝－3，那么这个函数的解析式是()A．B．C．D．y＝3xy＝－3xy＝13xy＝－13xB2．已知y与x成反比，当x＝3时，y＝4，那么y＝3时，x的值等于()A．4B．－4C．3D．－3Ay＝kx，y＝3xy＝－3xy＝13xy＝－13x随堂练习3．下面的函数是反比例函数的是()A．y＝3x＋1B．y＝x2＋2xC．D．y＝x2y＝2xD4．当路程s一定时，速度v与时间t之间的函数关系是()A．正比例函数B．反比例函数C．一次函数D．无法确定By＝x2y＝2x随堂练习5．某工人承包运输粮食的总数是w吨，每天运x吨，共运了y天，则y与x的关系式为_____,y＝wx是______函数．反比例6．若函数y＝(m－1)xm2－2是关于x的反比例函数，则m的值______．－1y＝wx随堂练习7．已知y＋1与x成反比例，当y＝1时，x＝12(1)求y与x的函数关系式；(2)当x＝3时，求y的值．解：(1)∵y＋1与x成反比例，∴设y＋1＝kx，∴y＝kx－1，把，y＝1代入上式中，得x＝121＝k12－1，∴k＝1，∴y与x的函数关系式为y＝1x－1；(2)当x＝3时，y＝13－1＝－23x＝12∴设y＋1＝kx，∴y＝kx－1，x＝121＝k12－1，y＝1x－1；y＝13－1＝－23随堂练习8.已知y=y1+y2，y1与(x－1)成正比例，y2与(x+1)成反比例，当x=0时，y=－3；当x=1时，y=－1，求：(1)y关于x的关系式；(2)当x=时，y的值.1212随堂练习解：（1）设y1=k1(x－1)(k1≠0)，(k2≠0)，221kyx则.2111kykxx∵x=0时，y=－3；x=1时，y=－1，－3=－k1+k2，2112k，∴k1=1，k2=－2.∴21.1yxx∴（2）把x=代入(1)中函数关系式，得y=1211.2221kyx2111kykxx2112k，21.1yxx1211.2课堂小结1、定义：一般地，如果两个变量x，y之间的关系可以表示成：（k为常数，k≠0）的形式，那么称y是x的反比例函数.xky2、注意：（1）常数k≠0；（2）自变量x不能为零（因为分母为0时，该式没意义）；（3）当可写为时注意x的指数为-1.xky1kxyxkyxky1kxy谢谢~