高斯公式 (2),高斯公式24个

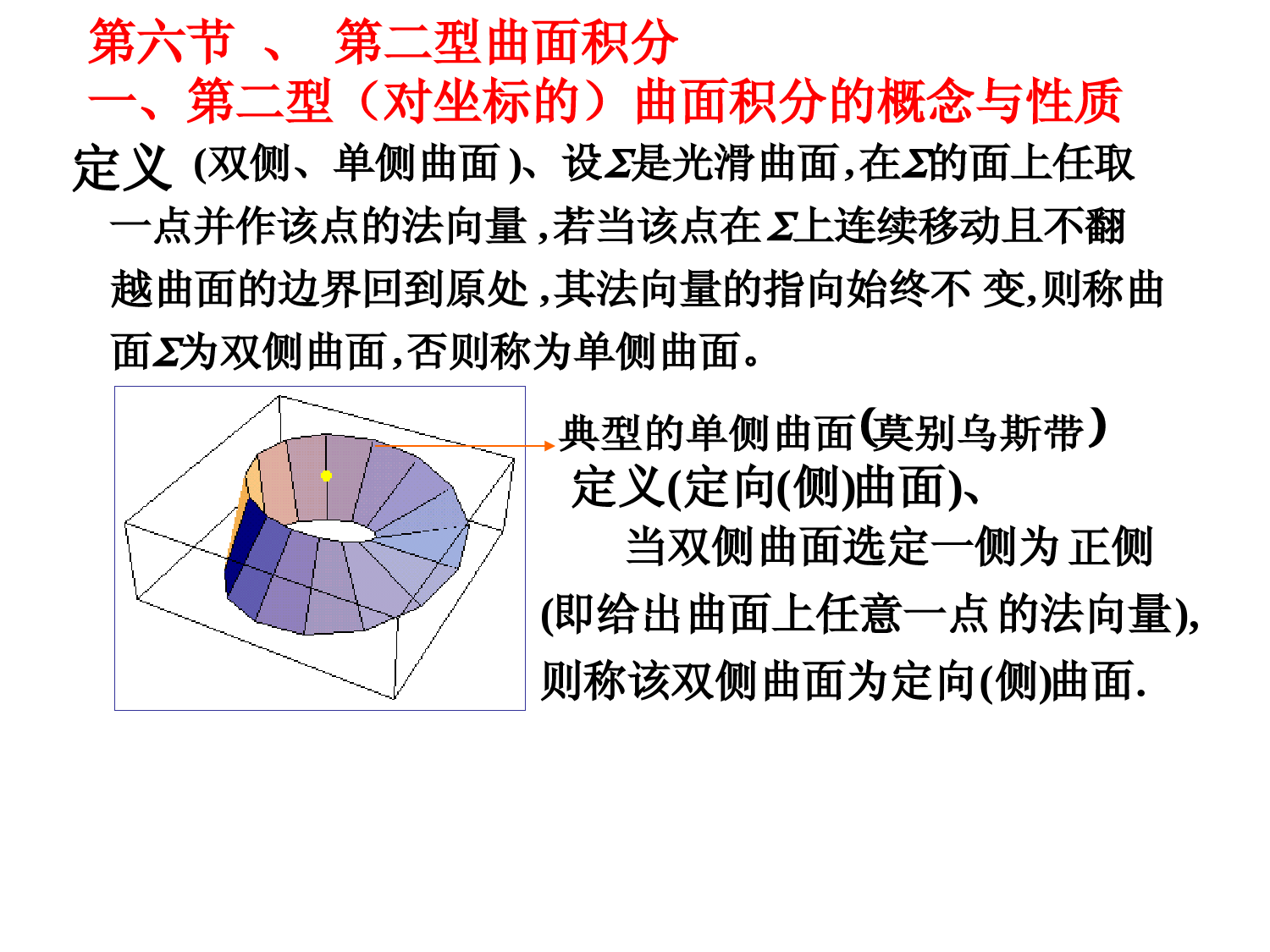
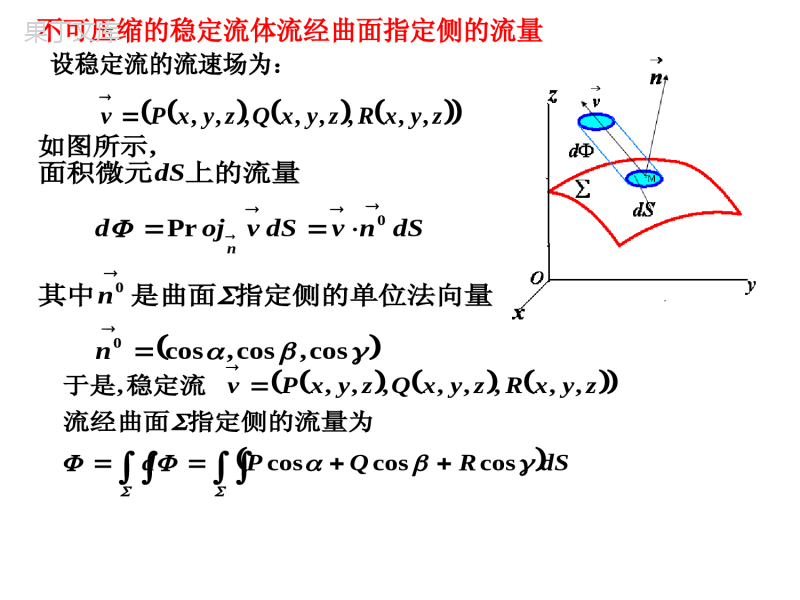
第六节、第二型曲面积分一、第二型（对坐标的）曲面积分的概念与性质莫别乌斯带典型的单侧曲面否则称为单侧曲面。为双侧曲面面则称曲变其法向量的指向始终不越曲面的边界回到原处上连续移动且不翻若当该点在一点并作该点的法向量的面上任取在是光滑曲面、设双侧、单侧曲面,,,,,)(、曲面侧定向定义))((.)(),(曲面侧则称该双侧曲面为定向的法向量即给出曲面上任意一点正侧当双侧曲面选定一侧为定义不可压缩的稳定流体流经曲面指定侧的流量zyxRzyxQzyxPv,,,,,,,,设稳定流的流速场为：,如图所示cos,cos,cosPr000nndSnvdSvojddSn指定侧的单位法向量是曲面其中上的流量面积微元dSRQPdzyxRzyxQzyxPvcoscoscos,,,,,,,,,指定侧的流量为流经曲面稳定流于是定义、:,,,,,,,,,)cos,cos,(cos,0别为分分上的三个第二型曲面积则曲面上的有界函数义在是定和指定侧上的单位法向量为曲面是双侧光滑曲面设zyxRzyxQzyxPndSzyxRdxdyzyxRdSzyxQdzdxzyxQdSzyxPdydzzyxPcos),,(),,(cos),,(),,(cos),,(),,(.]cos),,(cos),,(cos),,([),,(),,(),,(dSzyxRzyxQzyxPdxdyzyxRdzdxzyxQdydzzyxPdxdyzyxRdzdxzyxQdydzzyxP),,(),,(),,(.),,(),,(),,(:)),,(),,,(),,,((dxdyzyxRdzdxzyxQdydzzyxPzyxRzyxQzyxPv的流量为则通过有向曲面设稳定流的流速场为：0cos),,(),,(,0cos),,(),,(,0cos),,(),,(,222dSzyxRdxdyzyxRzdSzyxQdzdxzyxQydSzyxPdydzzyxPx则轴直与上每一点的法向量均垂显然：若则轴直与上每一点的法向量均垂显然：若则轴直与上每一点的法向量均垂显然：若第二型曲面积分的性质.)()()(222111212121dxdyRdzdxQdydzPdxdyRdzdxQdydzPdxdyRRdzdxQQdydzPP线性性质：)1(RdxdyQdzdxPdydzRdxdyQdzdxPdydz2121)(有限可加性：)2(.,RdxdyQdzdxPdydzRdxdyQdzdxPdydz则的相反侧曲面为设反向变号性：)3(二、第二型曲面积分的计算法.cos,cos,cos:,),,(,的方向余弦分别为的法向量处在点任取点设定向曲面为nPzyxP).()0(cos0cos下侧为上侧那么称如果).()0(cos0cos后侧为前侧那么称如果).()0(cos0cos左侧为右侧那么称如果面投影区域在设定向曲面为xoyDyxyxzzxy),(),,(::,那么是上侧如果xyDdxdyyxzyxRdxdyzyxR)],(,,[),,(:,那么是下侧如果xyDdxdyyxzyxRdxdyzyxR)],(,,[),,(面投影区域在设定向曲面为yozDzyzyxxyz,),(),,(:yzyzDDdxdyzyzyxPdydzzyxPdydzzyzyxPdydzzyxP],),,([),,(:,],),,([),,(:,那么是后侧如果那么是前侧如果xzxzDDdzdxzzxyxQdzdxzyxQdzdxzzxyxQdzdxzyxQ]),,(,[),,(:,]),,(,[),,(:,那么是左侧如果那么是右侧如果面投影区域在设定向曲面为xozDzxzxyyxz,),(),,(:)(法第二型曲面积分计算方定理:,"那么是上侧如果DdxdyyxzyxRdxdyzyxR)],(,,[),,(:,那么是下侧如果")],(,,[),,(DdxdyyxzyxRdxdyzyxR证明：,).1(是上侧时当,11cos),1,,(22yxyxzzzzndSzyxRdxdyzyxRcos),,(),,(由定义dSzzzyxRyx2211),,(dxdyzzzzyxzyxRyxDyx2222111)),(,,(DdxdyyxzyxR.)),(,,(,).2(是下侧时当,11cos),1,,(22yxyxzzzzndSzyxRdxdyzyxRcos),,(),,(由定义dSzyxRdxdyzyxRcos),,(),,(由定义dSzzzyxRyx2211),,(dxdyzzzzyxzyxRyxDyx2222111)),(,,(DdxdyyxzyxR.)),(,,(理可证。前侧、后侧的结论，同定理中，右侧、左侧；.,2222的外侧下半部分为球面其中计算Rzyxzdxdy、例1解DdxdyyxR222RrdrrrRd022220)sin()cos(zdxdyDdxdyyxR)(222RrdrrRd02220rdrrRR0222)(22022rRdrRR.32)(1130222123RrRR.141642:,)0),sin(,(22422所截下部分的上侧被柱面其中的流量定侧曲面的流体通过计算速度为yxzxyxevyx:解段平面上的投影为一直线在zox0)sin(dzdxyx4)2(:22zyDyozyz平面上的投影为在dzdxyxdydzeyx)sin(224dydzeyx224dydzeyzDzy22)2(44).1(416204202erdredr、例2dzdxyxdydzeyx)sin(224流量)(轴垂直上任意点的法向量与y第七节、高斯公式（Gauss）一、高斯公式dxdydzzRyQxPRdxdyQdzdxPdydzzyxRzyxQzyxP:,,,,,,,,,,2,1则的偏导数并且有连续上有定义在取外侧；所围成的有界闭区域是由分片光滑曲面设、高斯公式定理)(),,,(RQPA设向量场),,(RQPARdxdyQdzdxPdydz为向量场称zRyQxPAdivRQPAzRyQxP:),,(记为为向量场称:.),,()cos,cos,(cos0也可表示为的单位法向量处是在点设zyxndxdydzzRyQxPdSRQPdvAdivdSnA)coscoscos()2()1(0.的通量.的散度高斯公式.,2222222333的外侧球面为其中计算RzyxRzyxdxdyzdzdxydydzxdxdyzdzdxydydzxRRzyxdxdyzdzdxydydzxI33322233321dvzyxRGauss)(23222dddRR20004sin23456R、例1:解522232RR.),,(cos,cos,cos,)0(0)coscoscos(222222向量的方向余弦处的法在点是间的部分的下侧之及介于平面为锥面其中计算曲面积分zyxhhzzzyxdSzyx、例2:解..:,),(,::222上侧补充定向曲面hyxDDyxhz.:所围成的区域为及由dxdyzdzdxydydzxdSzyx222222)coscoscos(dvzyxdxdyzdzdxydydzxGauss)222(222dvzyxdxdyzdzdxydydzxGauss)222(222zdvydvxdv2220,xdvxyoz是奇函数面对称关于0,ydvyxoz是奇函数面对称关于zdvdxdyzdzdxydydzx222222202zyxhzdxdydzhdzzz022.22403hdzzhdxdyzdzdxydydzxhdxdyzdzdxydydzx2224222200224dxdyzhdxdyhhD242.224224hhhh..:,),(,:222上侧hyxDDyxhz、例3.)()()(,2222222的内侧是球面其中计算Rczbyaxxzdxdyxydzdxdydzx:解dvxzxyxxzdxdyxydzdxdydzxzyx])2()2()[(2222由高斯公式dvxxx)222(xdv6)(6Vx.834633RaRa第八节斯托克斯（Stokes）公式一、斯托克斯公式dxdyyPxQdzdxxRzPdydzzQyRRdzQdyPdxzyxRzyxQzyxP:.),,(),,,(),,,()2().("",)1(则导数的某邻域内有连续的偏曲面在包含函数见图所示右手法则的方向满足边界曲线的侧与它的是分片光滑的有向曲面设、斯托克斯公式定理)(dSRQPzyxRQPzyxdxdydzdxdydzcoscoscos的方向余弦。法向量处的上点是在其中：nzyx),,(cos,cos,cos.),,,(是有向闭曲线设向量场RQPF的沿闭曲线为向量场称曲线积分),,(RQPFRdzQdyPdx的为向量场称),,(RQPFRQPzyxkjiFrot处的上点为在设),,()cos,cos,(cos0zyxn处的上点为在),,()cos,cos,(cos0zyxdSnFrotdsF00:可表示为则.环量.旋度斯托克斯公式.单位法向量.单位切向量:旋度的物理意义),0,0(:角速度),,(:zyxr向径rv:线速度jxiyzyxkji000:xyzyxkjivrot线速度的旋度.2),0,0(22k.度的两倍线速度的旋度等于角速.,1,3322针方向轴正方向向下看呈逆时由的交线与平面是圆柱面其中计算zxzyxdzxdyydx、例1:解..1:,),(:22上侧yxDDyxxz.21cos,0cos,21cos),1,0,1(ndSxyzyxdzxdyydx133coscoscos33dSxyzyxdzxdyydx133coscoscos33dSxyzyxdSxyzyx1331012113321021dS]600[21cos)(2626DAdS.6)(6DA..1:,),(:22上侧yxDDyxxz))(,(cos21DA、例2.,,)0,0(22)()()(22222222222时针方向取逆轴的正方向看去若从的交线与柱面是球面其中曲线积分利用斯托克斯公式计算zzRrrxyxRxzyxdzyxdyzxdxzyI:解,部分所围成的侧被为球面的上取RxzyxzyxF2),,(:222令.2;2;22zFyFRxFzyx),,,(:zyRxn的法向量为),,,(:zyRxn的法向量为:的方向余弦为n;)(cos222RRxzyRxRx;)(cos222RyzyRxy;)(cos222RzzyRxz利用斯托克斯公式dzyxdyzxdxzyI)()()(222222dSyxzxzyzyx222222coscoscosdSyxzxzyzyxRzRyRRx222222dzyxdyzxdxzyI)()()(222222dSyxzxzyzyxRzRyRRx222222dSRzyxRyzxRRxzy])22()22()22[(.22)(2ydSzdSdSyz.02,,ydSyxoz于是是奇函数平面对称关于由于zdSI2dSzcoscos12dxdyzcos12dxdyzRz2dxdyR2.222222RrdxdyRrxyx二、空间曲线积分与路径无关的条件、定理1).,(),,()4();(),,()3(;,0)2(;),,(,0)1(,,,),,(RdzQdyPdxduuRQPFRdzQdyPdxRdzQdyPdxRQPFGRdzQdyPdxGzyxRQPzyxkjiFrotGGRQPGRQPFBAAB使得即存在是势场即是保守场内任一简单闭曲线是其中内下述四个命题等价则在内有连续的偏导数在和函数上的向量场是定义在单连通区域设.0,,),,(),,,(),,,(,内恒成立在有关界曲线的边而仅与无关内与所取曲面在则曲面积分内具有一阶连续偏导数在是空间二维单连通区域设GzRyQxPFdivGRdxdyQdzdxPdydzGzyxRzyxQzyxPG三、沿任意闭曲面的曲面积分为零的条件、定理2