常用微分公式,常用微分公式24个
本作品内容为常用微分公式,格式为 doc ,大小 361984 KB ,页数为 11页

(".§1-3微分公式..(甲)基本函数的微分公式(1)=nxn\uf02d1,n\uf0ceN。(2)dxdxnxnNnn\uf03d\uf0ce\uf02d111,。(3)=0,其中c为常数。(4)(sinx)/=cosx(5)(cosx)/=\uf02dsinx另一种表示:\uf081(xn)/=nxn\uf02d1\uf082=\uf083(c)/=0证明:(2)设a为f(x)=定义域中的任意点,则f/(a)=====()=()(4)设a为任意实数,f(x)=sinx==计算f/(a)==()=cosa。(1)(3)(5)自证(乙)导数的四则运算(1)f(x)与g(x)为可微分的函数。\uf0def(x)+g(x)为可微分的函数。且(f(x)+g(x))=(f(x))+(g(x))成立。另一种表示:(f(x)+g(x))/=f/(x)+g/(x)证明:令h(x)=f(x)+g(x),设a为h(x)定义域中的任一点h/(a)===(+)=()+()=f/(a)+g/(a)例:求?推论:(f1(x)+f2(x)+...+fn(x))=(2)设f(x)为可微分的函数。\uf0decf(x)为可微分的函数。且(cf(x))=c,特别c=\uf02d1时,(\uf02df(x))=\uf02d。(3)ddxfxgxdfxdxdgxdx(()())()()\uf02d\uf03d\uf02d,另一种表示:(f(x)\uf02dg(x))/=f/(x)\uf02dg/(x)..(4)(c1f1(x)+c2f2(x)+...+cnfn(x))=c1(f1(x))+c2(f2(x))+...+cn(fn(x))例如:(1)(anxn+an\uf02d1xn\uf02d1+...+a1x+a0)(2)(3x5\uf02d2x3+4)/=?(5)f(x),g(x)为可微分的函数。\uf0def(x)g(x)为可微分的函数。且(f(x)\uf0d7g(x))=(f(x))\uf0d7g(x)+f(x)\uf0d7(g(x))另一种表示:(f(x)\uf0d7g(x))/=f/(x)\uf0d7g(x)+f(x)\uf0d7g/(x)证明:例如:试求ddxxxxx(()())?223321\uf02b\uf02d\uf02d\uf02b\uf03d下面我们要推导例2的一般情形:(a)ddxfxfxfx(()()())123\uf02b\uf02b=dfxdxfxfxfxdfxdxfxfxfxdfxdx123123123()()()()()()()()()\uf02b\uf02b(b)ddxfffdfdxffffdfdxnnn()121212\uf0d7\uf0d7\uf0d7\uf03d\uf0d7\uf0d7\uf0d7\uf02b\uf0d7\uf0d7\uf0d7\uf02b\uf0d7\uf0d7\uf0d7(逐次轮流微分)(c)如果ffffn12\uf03d\uf03d\uf0d7\uf0d7\uf0d7\uf03d,则可得ddxfxnfxdfxdxnn((())(())()\uf03d\uf02d1例如:试求()xx2523\uf02b\uf02b的导数。[例題1]证明dxdxrxrQrr\uf03d\uf0ce\uf02d\uf02b1,。..(6)若f(x),g(x)在x=a可微分,且ga()\uf0b90,则ddxfxgxfagafagagaxa(()())()()()()(())//\uf03d\uf03d\uf02d2。因此可得:(()())()()()()(())///fxgxfxgxfxgxgx\uf03d\uf02d2若f(x)=1,则()/=例如:试求xxx2211\uf02d\uf02b\uf02b的导函数。例如:求()/=?例如:设r为负有理数,证明dxdxrxrr\uf03d\uf02d1。结论:若设r为有理数,则dxdxrxrr\uf03d\uf02d1。[例題2]求下列各函数的导函数:(1)(x2+2x)(x2+3x+2)(2)(x\uf02d2)3(x2\uf02d1)(3)(x2+x+1)(4x3+x\uf02d4)(x+3)(3)(4)Ans:(1)4x3+15x2+16x+4(2)(x\uf02d2)2(5x2\uf02d4x\uf02d3)(3)(2x+1)(4x3+x\uf02d4)(x+3)+(x2+x+1)(12x2+1)(x+3)+(x2+x+1)(4x3+x\uf02d4)(4)(5)[例題3]请利用(sinx)/=cosx,(cosx)/=\uf02dsinx的结果证明:(tanx)/=sec2x,(secx)/=secx\uf0d7tanx..(練習1.)试求下列的导函数:(1)x3\uf02d6x2+7x\uf02d11(2)(x3+3x)2(2x+1)(3)(x+1)(2x2+2)(3x2+x+1)(4)(2x3+x+1)5Ans:(1)3x2\uf02d12x+7(2)2(x3+3x)(3x2+3)(2x+1)+2(x3+3x)(3)(2x2+2)(3x2+x+1)+(x+1)\uf0d7(4x)\uf0d7(3x2+x+1)+(x+1)(2x2+2)\uf0d7(6x+1)(4)5(2x3+x+1)4\uf0d7(6x2+1)(練習2.)求下列各函数的导函数。(1)f(x)=(2)f(x)=(3)f(x)=(4)f(x)=Ans:(1)(2)(3)\uf0d7(12x2+6x+2)(4)(練習3.)证明ddxxx(cot)csc\uf03d\uf02d2,ddxxxx(csc)csccot\uf03d\uf02d(丙)连锁法则(1)合成函数:(a)设fxxxgyy(),()\uf03d\uf02b\uf02b\uf03d231,则gfxxx(())\uf03d\uf02b\uf02b231。xxxxxfg\uf0be\uf0ae\uf0be\uf02b\uf02b\uf0be\uf0ae\uf0be\uf02b\uf02b22311,()()gfxxx\uf06f\uf03d\uf02b\uf02b231所以()()gfx\uf06f为x的函数。(b)gffg\uf06f\uf06f\uf0b9(2)连锁法则:既然()()gfx\uf06f为x的函数,我们就可以讨论ddxgfx()()?\uf06f\uf03d例:设fxxgxy(),()\uf03d\uf02b\uf03d232,则()()(())()gfxgfxx\uf06f\uf03d\uf03d\uf02b232利用ddxfxnfxdfxdxnn((())(())()\uf03d\uf02d1,可得ddxxxx(())()2322322\uf02b\uf03d\uf02b\uf0d7=ddygydfxdxyx()()\uf03d\uf02b\uf0d722上式并不是巧合,一般的情形亦是如此。..定理:(连锁法则ChainRule)若f(x),g(y)都是可微分的函数,则合成函数()()gfx\uf06f亦可微分,而且ddxgfxdgydydfxdxgfxgfxfxyfx(()())()()()()(())()()///\uf06f\uf06f\uf03d\uf0d7\uf03d\uf03d或。[例題4]求?一般情形:nN\uf0ce,f(x)可微分,求=?[例題5]求f(x)=sin2x的导函数。Ans:2sinx\uf0d7cosx..[例題6]求下列函数的导函数:(1)fxx()tan\uf03d3(2)(3)fxx()tan\uf03d\uf02d12Ans:(1)3tan2x\uf0d7sec2x(2)\uf02d5csc5x\uf0d7cot5x(3)(練習4.)设n为正整数而f(x)为可微分的函数,试用连锁律去计算(f(x))n的导函数。Ans:n(f(x))n\uf02d1\uf0d7f/(x)(練習5.)求(=?Ans:\uf0d7(4x3+6x\uf02d1)(練習6.)\uf05b\uf05d()?/xx2231\uf02b\uf02b\uf03dAns:(練習7.)求下列各小题y/(1)yxx\uf03dsin(2)yx\uf03dcos3(3)yx\uf03d\uf02b521cos()(4)yxx\uf03dsincos4(5)yx\uf03d\uf02b12sinAns:(1)sincosxxx\uf02b(2)\uf02d32cossinxx(3)\uf02d\uf02b1021sin()x(4)coscossinsinxxxx444\uf02d(5)sincossinxxx12\uf02b(練習8.)计算下列各小题:(1)(x\uf0d7)/=?Ans:(2)()=?Ans:(3)求f(x)=的导函数。Ans:f/(x)=(練習9.)设可微函数f(x)满足f()=x,则f/(0)=?Ans:2[例題7]试求?..(練習10.)试求的导函数。Ans:(練習11.)求f(x)=的导函数。Ans:f/(x)=(練習12.)\uf028\uf029fxxx()\uf03d\uf02b\uf02b2134,求f/(3)=?(練習13.)设y=(x+)10,试求=?Ans:\uf0d7(x+)10[例題8]求斜率为2,而与曲线y=f(x)=x3\uf02dx2+相切之直线方程式。Ans:4x\uf02d2y+3=0,2x\uf02dy\uf02d3=0(練習14.)求过曲线y=f(x)=x3+x2\uf02d2的点,而斜率最小的切线方程式。Ans:y+=(\uf02d1)(x+1)(練習15.)求通过y=x3\uf02d3x2\uf02d4x\uf02d1上x=1处之切线与法线方程式。Ans:7x+y=0,x\uf02d7y\uf02d50=0(練習16.)函数f(x)=的图形上以(0,\uf02d1)为切点的切线斜率为。Ans:1[例題9]设拋物线y=ax2+bx+c与直线7x\uf02dy\uf02d8=0相切于点(2,6),而与直线x\uf02dy+1=0相切,求a,b,c之值。Ans:a=3,b=\uf02d5,c=4(85日大自然)..[例題10]直角坐标上,给定一曲线\uf047:y=x3\uf02d3x2,自点P(2,\uf02d5)向\uf047所作的切线方程式。Ans:3x+y\uf02d1=0,15x\uf02d4y\uf02d50=0(練習17.)过原点且与曲线y=x3\uf02d3x2\uf02d1相切之直线方程式。Ans:y=\uf02d3x,y=。(練習18.)设拋物线y=ax2+bx+c过点(1,1),且与直线x\uf02dy=3相切于(2,\uf02d1)。求a,b,c之值Ans:a=3,b=\uf02d11,c=9[例題11]设a,b,c为实数,已知二曲线y=x2+ax+b与y=\uf02dx3+c在点A(1,\uf02d2)处相切,L为两曲线在A点的公切线,试求(1)a,b,c(2)求L的方程式。Ans:(1)a=\uf02d5,b=2,c=\uf02d1(2)3x+y\uf02d1=0(練習19.)拋物线\uf047:y=p(x)的对称轴平行于y轴,且\uf047与x轴交于点(2,0),并在x=1时与函数y=x4+1的图形相切,试求p(x)=?Ans:p(x)=\uf02d6x2+16x\uf02d8..(練習20.)求y=x3\uf02d3x,y=x3\uf02d3x+32两曲线的公切线方程式。Ans:9x\uf02dy+16=0综合练习1.(1),求=?(2)fxxx()\uf03d\uf02d\uf02b11,求f/()=?(3)f(x)=x3(x3+5x)10,求f/(x)Ans:(1)\uf028\uf029\uf028\uf029\uf028\uf029dydxxxxx\uf03d\uf02d\uf02d\uf02b\uf02b\uf02b33512403412224(2)(3)\uf028\uf029\uf028\uf029xxxx395353365\uf02b\uf02b2.求下列各函数的导函数:(1)fxx()()\uf03d\uf02b2531(2)fxxx()()\uf03d\uf02b\uf02b22521(3)fxxx()()()\uf03d\uf02b\uf02b211425Ans:(1)fxxx'()()\uf03d\uf0d7\uf02b1013223(2)fxxxx'()()()\uf03d\uf02d\uf02b\uf02b10212426(3)fxxxxx'()()(8)()\uf03d\uf02b\uf02d\uf02d\uf02b211012132263.试求下列个函数的导函数:(1)fxx()sin\uf03d(2)fxxx()cos()\uf03d\uf02d\uf03c\uf03c\uf070\uf07022(3)(4)(5)fxx()sin()\uf03d23(6)fxxx()tansec\uf03d\uf02d22(7)(8)fxxx()sincos\uf03d2Ans:(1)(2)(3)\uf02d1221xxsec(4)(5)(6)0(7)(8)sinsecsinxxx2\uf02b4.(1)设fxax()\uf03d\uf02d21,若f/(1)=2,则a=?(2)设fxxx()\uf03d\uf02b\uf02d2135,则f/(2)=?Ans:(1)2(2)5.设yu\uf03d\uf02b34,uxx\uf03d\uf02b22,求dydx=?Ans:62122xxx()()\uf02b\uf02b6.求fxx()()\uf03d\uf02d221在(1,0)的切线方程式与法线方程式。Ans:y=0,x=17.曲线yxxx\uf03d\uf02b\uf02b231在x=\uf02d1处之切线方程式。Ans:2x+y+3=0..8.设f(x)=x3+ax2+b,abR,\uf0ce,若y=f(x)之图形通过点(1,4)且在此点的斜率为\uf02d3,则求a,b之值为何?Ans:a=\uf02d3,b=69.若直线y=x与曲线y=x3\uf02d3x2+ax相切,试求a=?Ans:a=1或10.过点(,)223\uf02d,且与曲线yxx\uf03d\uf02d133相切的直线有几条?其斜率分别为何?Ans:(1)3(2)0,3\uf0b12.",)
提供常用微分公式,常用微分公式24个会员下载,编号:1700757865,格式为 docx,文件大小为11页,请使用软件:wps,office word 进行编辑,PPT模板中文字,图片,动画效果均可修改,PPT模板下载后图片无水印,更多精品PPT素材下载尽在某某PPT网。所有作品均是用户自行上传分享并拥有版权或使用权,仅供网友学习交流,未经上传用户书面授权,请勿作他用。若您的权利被侵害,请联系963098962@qq.com进行删除处理。

 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载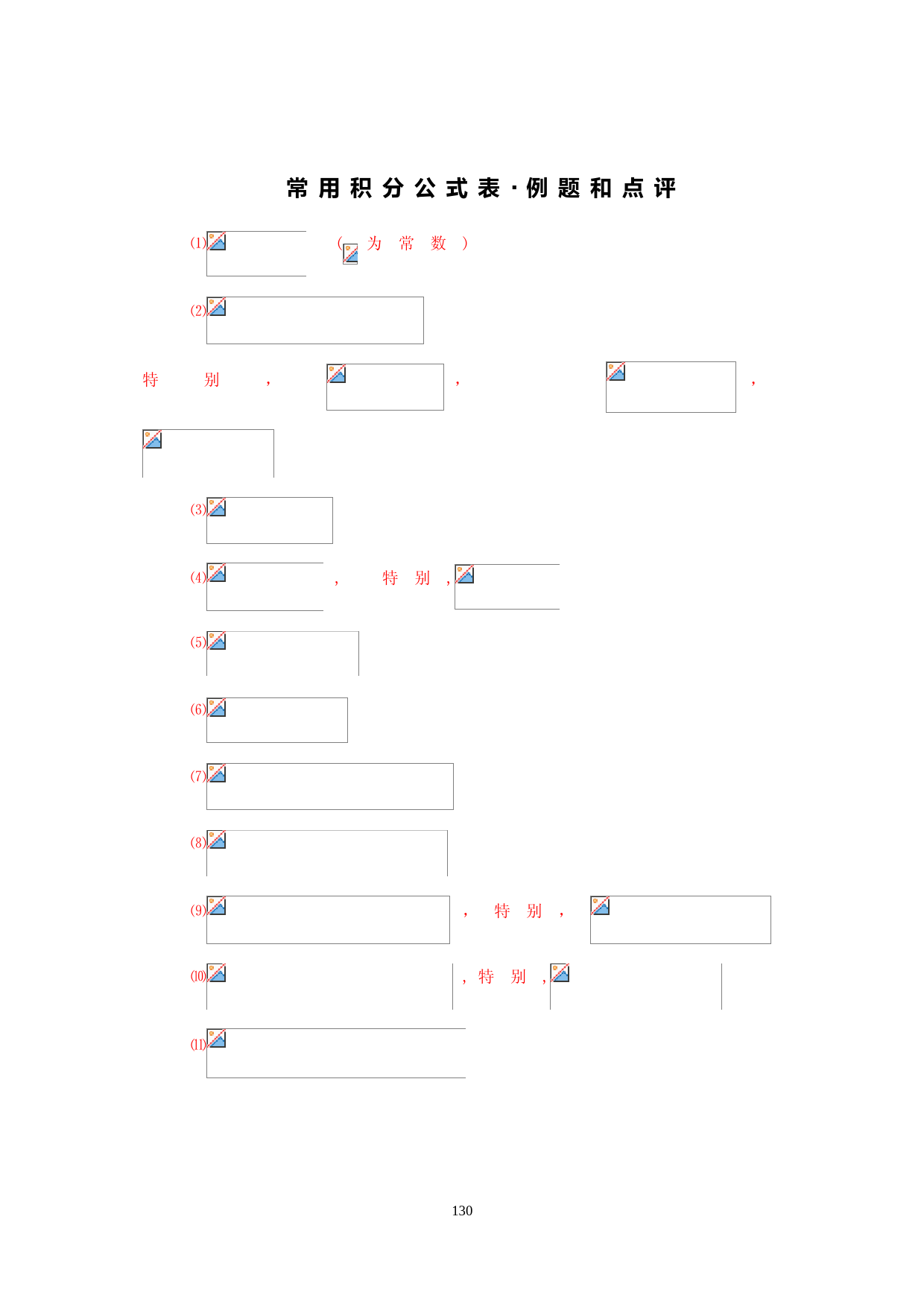 下载
下载 下载
下载 下载
下载 下载
下载