高斯公式 (1),高斯公式1+2+3+...+197+198+199





高斯(Gauss)公式及其应用牛顿—莱布尼兹公式bafxdxFbFa()LDQPdxdyPdxQdyxy格林公式立体与其表面曲面上积分间的关系?21.高斯(Gauss)公式()(,,)(,,)(,,)PxyzQxyzRxyz设空间闭区域是由光滑或分片光滑曲面所围成,函数、、在上具有一阶连续偏导数,则有dvzRyQxP)(RdxdyQdzdxPdydz.的整个边界曲面的外侧是这里定理33Gauss公式的实质揭示了空间闭区域上的三重积分与其边界曲面上的曲面积分之间的关系..)coscoscos()(dSRQPdvzRyQxP由两类曲面积分之间的关系知42.简单应用22103()().xydxdyyzxdydzxyzz计算曲面积分,其中为柱面及平面,所围成的空间闭区域的整个边界曲面的外侧例15解0(),,,PyzxQRxyxozy,0,0,zRyQzyxPdxdydzzy)(原式(sin)zdddz.29(利用柱面坐标)311dzzdd103020)sin(使用Guass公式时应注意:1.RQP,,是对什么变量求偏导数;2.是否满足高斯公式的条件;3.Σ是取闭曲面的外侧..),,(cos,cos,cos)0(0)coscoscos(2222222处的法向量的方向余弦在是之间的部分的下侧,及介于平面为锥面其中,计算曲面积分例zyxhhzzzyxdSzyx解)(:2221hyxhz补充曲面不是封闭曲面,为利用高斯公式取上侧,11构成封闭曲面外侧,1围成空间区域,,上使用高斯公式在由第二型曲面积分的定义222xdydzydzdxzdxdy原式xyzo1h12222()xdxdyydzdxzdxdyxyzdv}.),{(222hyxyxDxy其中220(),xyhxyDdxdyxydz由对称性1hxyD222()xyhxyDdxdyxyzdz222xyhxyDdxdyzdz222412()xyDhxydxdyhxyzo12zdxdyxyDdxdyh2.4h故所求积分为421h4h.214h1222xdydzydzdxzdxdy1yozzox在和面上投影面积为零1原式1222xdydzydzdxzdxdy2232222()(2)0.xzdydzxyzdzdxxyyzdxdyzaxy练习计算曲面积分,其中为半球体的整个表面曲面的外侧zyxyRzyxQxzP23222,,222yxzzRyQxP2220zaxy:222222420005().sin..sin25axyzdvrrdrddddrdra原式(球面坐标)解思考题曲面应满足什么条件才能使高斯公式成立?思考题解答曲面应是分片光滑的闭曲面.作业:P.174习题10-61.(1),(2),(4)2.(2)
提供高斯公式 (1),高斯公式1+2+3+...+197+198+199会员下载,编号:1701026978,格式为 xlsx,文件大小为15页,请使用软件:wps,office Excel 进行编辑,PPT模板中文字,图片,动画效果均可修改,PPT模板下载后图片无水印,更多精品PPT素材下载尽在某某PPT网。所有作品均是用户自行上传分享并拥有版权或使用权,仅供网友学习交流,未经上传用户书面授权,请勿作他用。若您的权利被侵害,请联系963098962@qq.com进行删除处理。

 下载
下载 下载
下载 下载
下载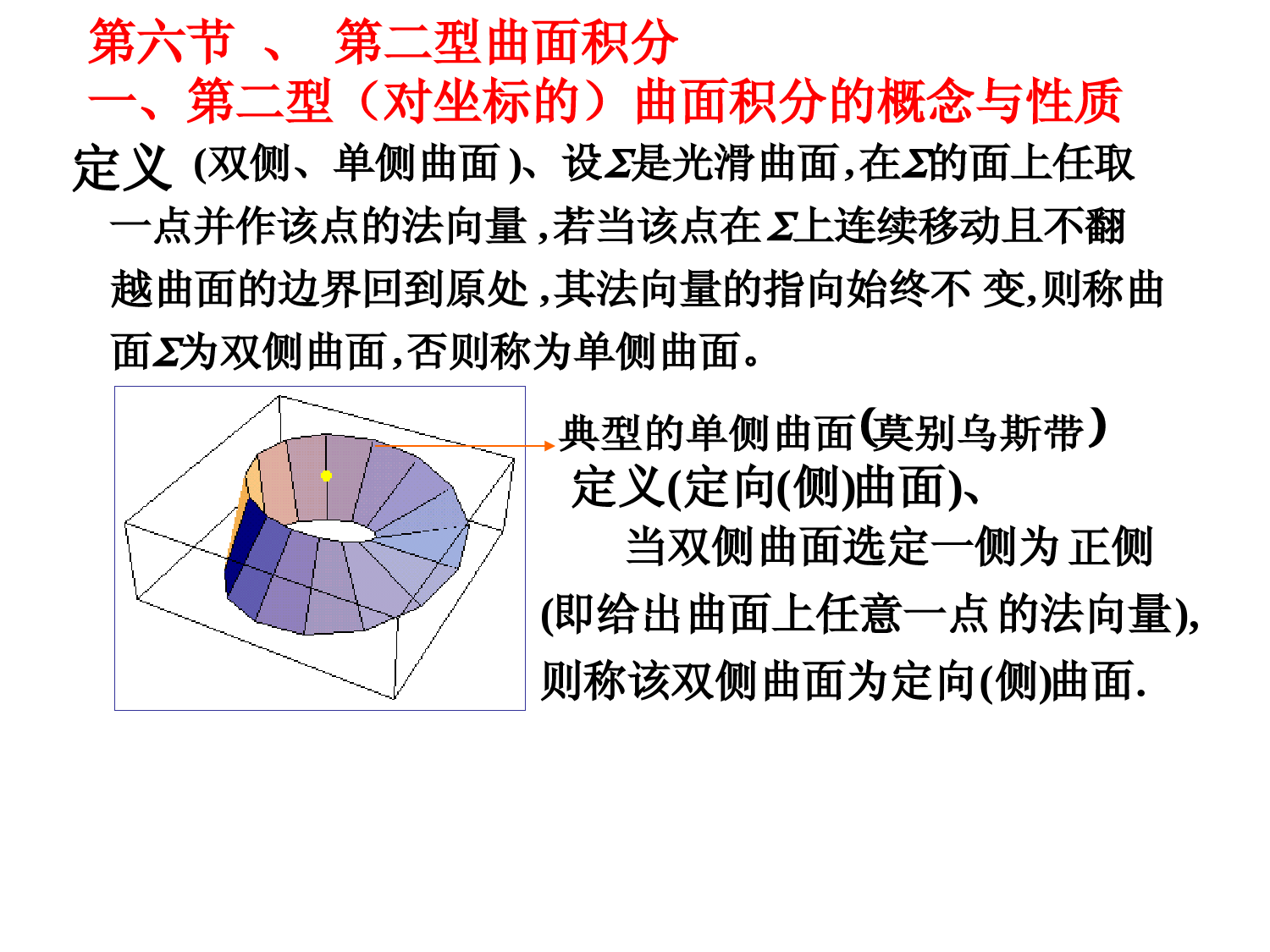 下载
下载