高等数学-高斯公式,高等数学高斯公式



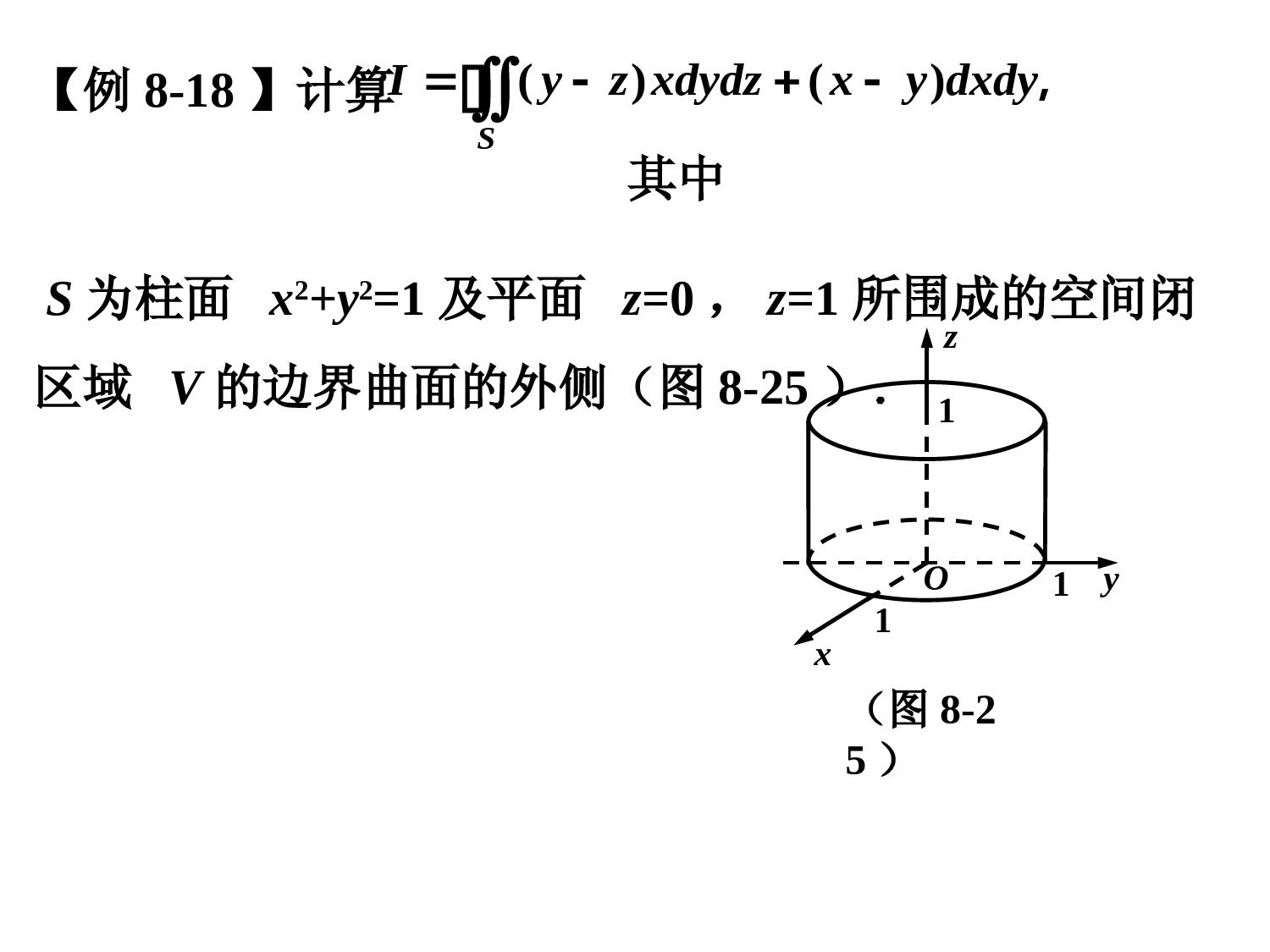
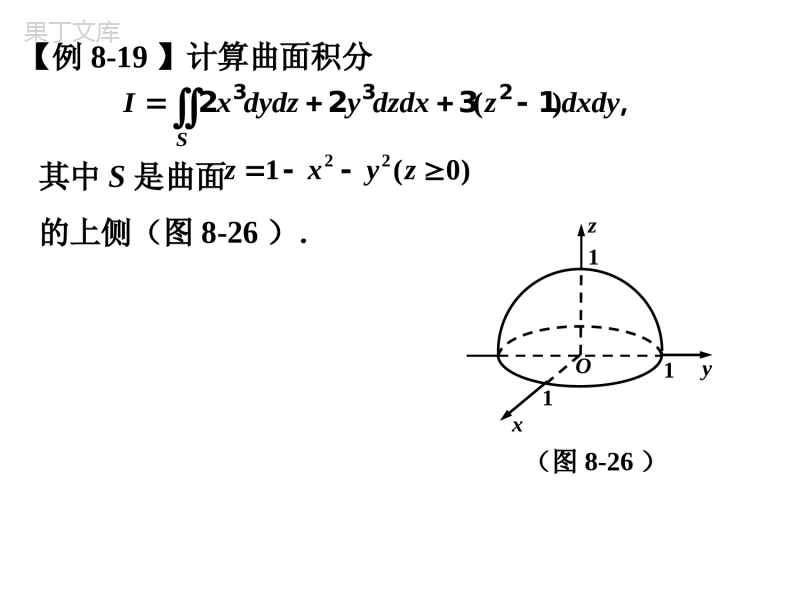
8.4高斯公式,斯托克斯公式格林公式建立了第二类平面曲线积分与二重积分的联系;高斯公式建立了第二类曲面积分与三重积分的联系;斯托克斯公式建立了第二类空间曲线积分与曲面积分的联系.高斯公式(,,),(,,),(,,),dddddd()ddd.div(),div(),dddd8(3ddSVVVSPxyzQxyzRxyzVPQRPyzQxzRxyxyzxyzSPQRAAMAMxyzPyzQxzRxy设空间闭区域是由光滑或分片光滑的封闭曲面所围成的单连通区域,函数在上有一阶连续偏导数则其中取外侧令称为在点处的则定理散度div)dddSAxyz【例8-18】计算其中S为柱面x2+y2=1及平面z=0,z=1所围成的空间闭区域V的边界曲面的外侧(图8-25).()()SIyzxdydzxydxdy,(图8-25)Ox1yz11【例8-19】计算曲面积分()SIxdydzydzdxzdxdy3322231,其中S是曲面的上侧(图8-26).)0(122zyxzOxyz111(图8-26)【例8-20】设函数f(u)具有连续导数,计算[()][()]SIxdydzyyfyzdzdxzzfyzdxdy333,其中S是锥面和球面与xyz22122zyxxyz224所围立体的表面外侧(图8-27).1Oxyz2(图8-27)224xyz221xyz斯托克斯(Stokes)公式.(,,),(,,),(,,)()dd()dd()dd84LSLSLLSPxyzQxyzRxyzSPdxQdyRdzRQPRQPyzzxxyyzzxxy设为分段光滑的空间有向闭曲线,为以为边界的分片光滑有向曲面,的正向与的法向量构成右手系,函数在内有一阶连续偏导数,则有定理0ddddddddd()coscoscosd()(cos,cos,cos)LSSyzzxxyPxQyRzxyzPQRSxyzPQRnS第二类曲面积分第一类曲面积分为与曲面的侧一致的单位法向量【例8-21】计算曲线积分其中L为平面x+y+z=1被三个坐标面所截得的三角形S的整个边界,其正方向与这个三角形上侧的法向量成右手系.LydzxdyzdxI,(图8-28)Oxyz111LS【例8-22】计算()()(),LIyzdxzxdyxydz22222223其中L是平面x+y+z=2与柱面的交线,从z轴正向看去L是逆时针(图8-29).1yxOxyzL(图8-29)作业:习题8-41(3)(4)2346(3)(4)关于斯托克斯公式的一些讨论(,,),rot(,rot((,,)ddd()dLSAPQRAAijkRQPRQPAxyzyzzxxyPQRPxQyRzrotAS设)为的旋度即)=则1111rot((,,)(rot()0.,,:rot(rot((rot()0,rot(rot(rot(ddSVSSSSRQPRQPAyzzxxydivASSSSVAdSAdSdivAdVAdSAdSAdSPxQ)则)设曲面与曲面有公共的边界曲线则与可围成立体由高斯公式)))则)))即1d()drot(:LSSyRzrotASAdSS)这说明第二类空间曲线积分写成斯托克斯公式时,与曲面的取法无关.
提供高等数学-高斯公式,高等数学高斯公式会员下载,编号:1701026979,格式为 xlsx,文件大小为12页,请使用软件:wps,office Excel 进行编辑,PPT模板中文字,图片,动画效果均可修改,PPT模板下载后图片无水印,更多精品PPT素材下载尽在某某PPT网。所有作品均是用户自行上传分享并拥有版权或使用权,仅供网友学习交流,未经上传用户书面授权,请勿作他用。若您的权利被侵害,请联系963098962@qq.com进行删除处理。

 下载
下载 下载
下载 下载
下载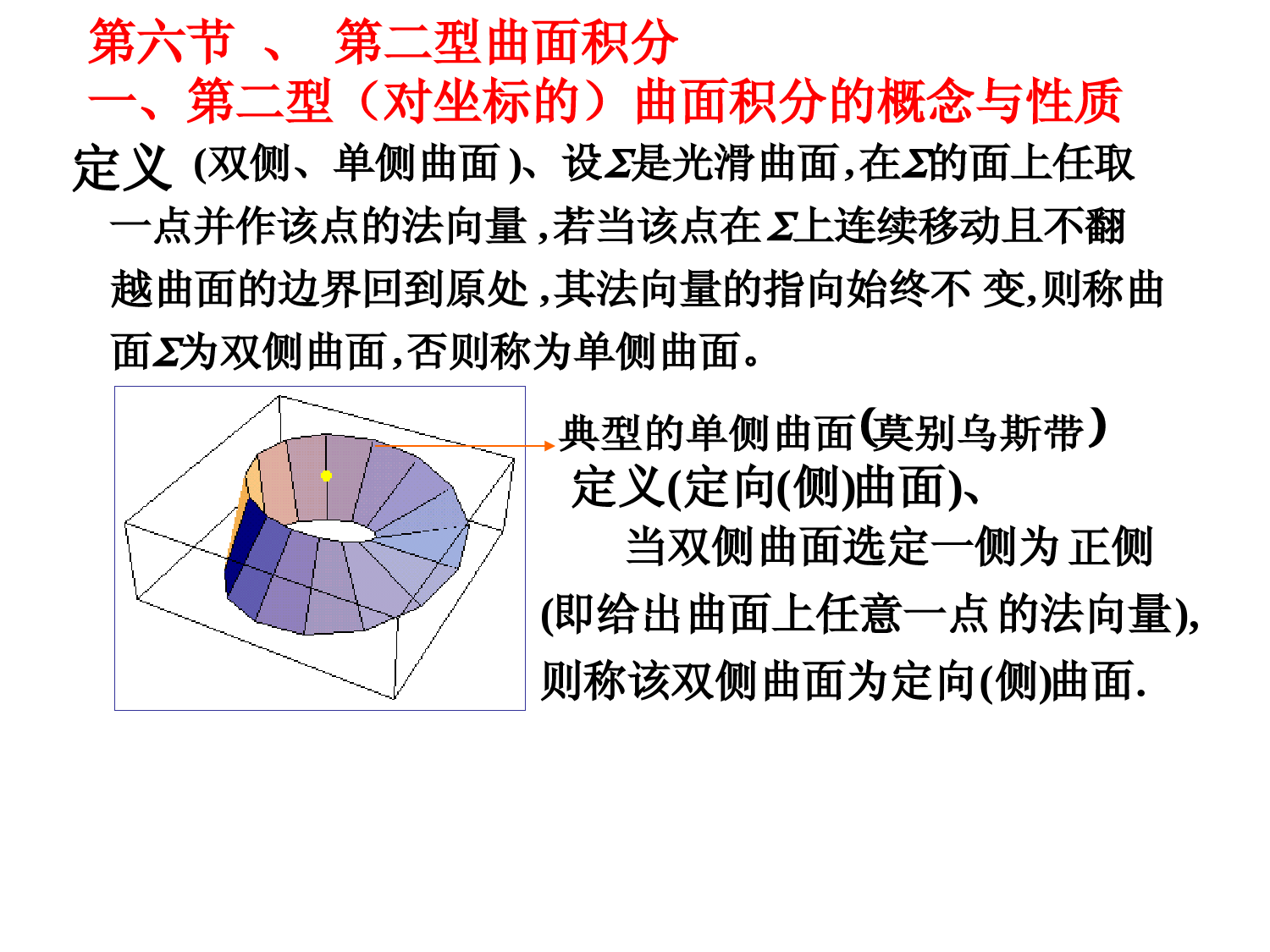 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载