二次函数的顶点式,二次函数的顶点式表达式

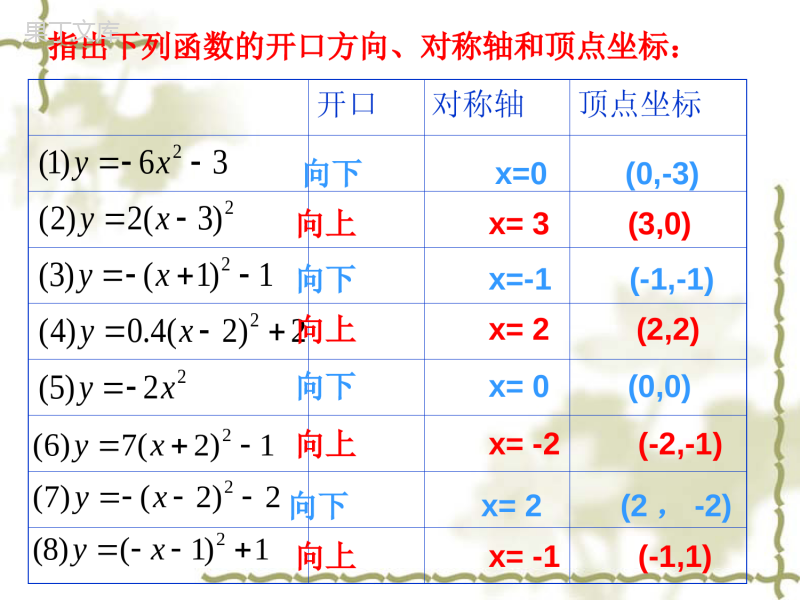
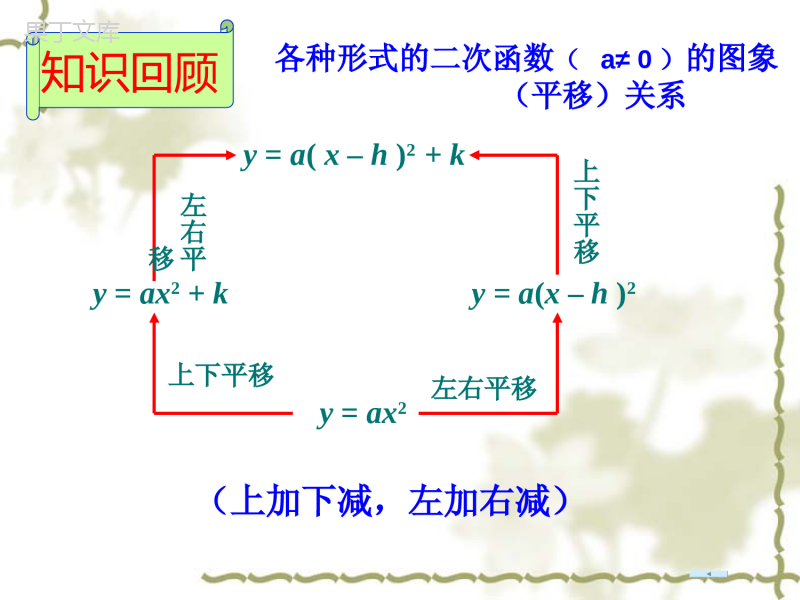
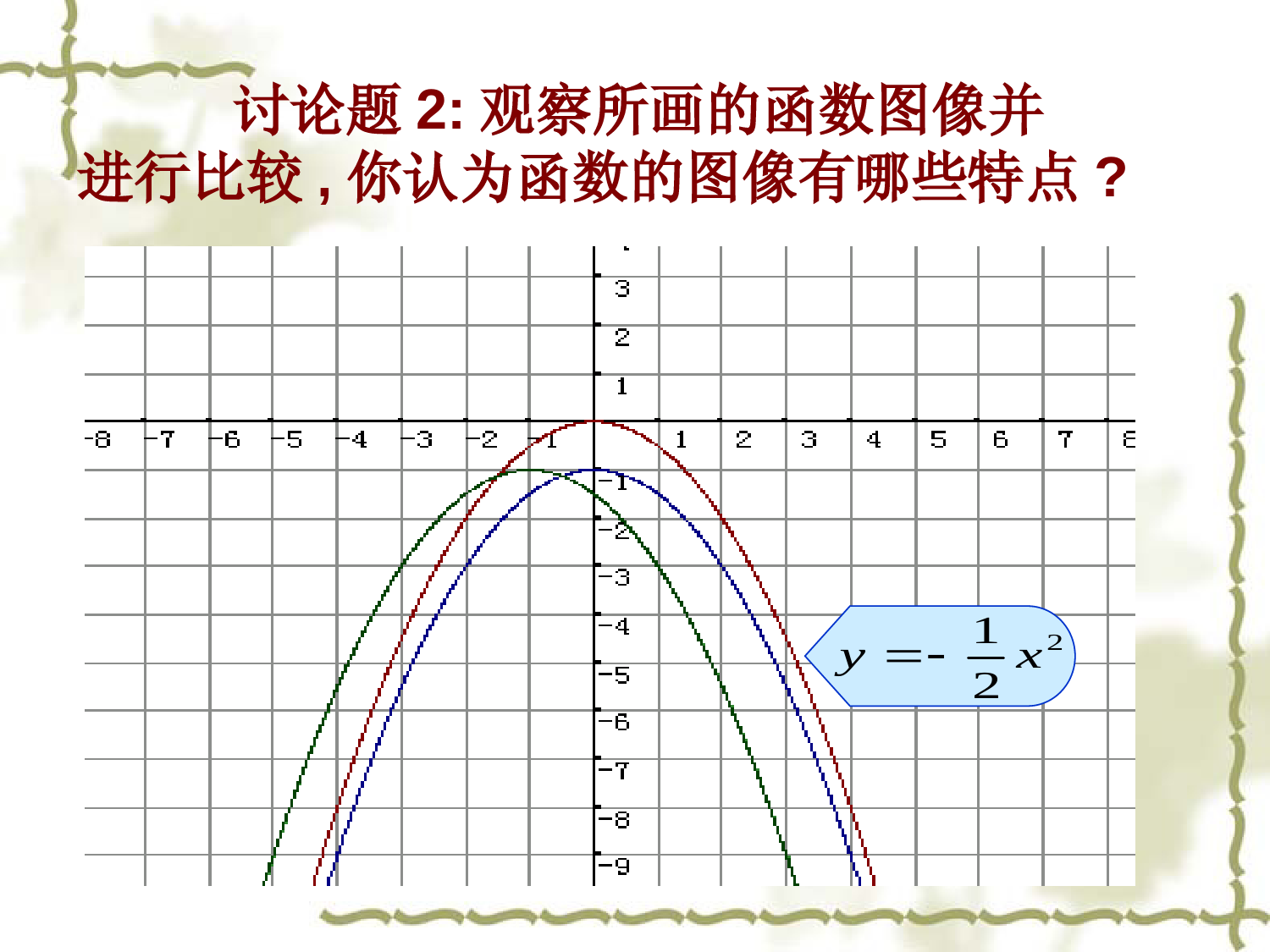
盛家坝中学刘祖芹开口对称轴顶点坐标222222)5(2)2(4.0)4(1)1()3()3(2)2(36)1(xyxyxyxyxy1)1()8(2)2()7(1)2(7)6(222xyxyxy向下x=-1(-1,-1)向下x=0(0,-3)向上x=3(3,0)向上x=2(2,2)向下x=0(0,0)向下x=2(2，-2)向上x=-2(-2,-1)向上x=-1(-1,1)指出下列函数的开口方向、对称轴和顶点坐标：y=ax2y=ax2+ky=a(x–h)2y=a(x–h)2+k上下平移左右平移上下平移左右平移（上加下减，左加右减）各种形式的二次函数（a≠0）的图象（平移）关系知识回顾讨论题2:观察所画的函数图像并进行比较,你认为函数的图像有哪些特点?221xy一、由顶点式说性质：说出下列抛物线的开口方向、对称轴、增减性及最值：（1）y=2(x+3)2+5;（2）y=－3(x－1)2－2;（3）y=4(x－3)2+7;解：（1）a=2>0开口向上，对称轴为x=－3，当x≤-3时，y随x的增大而减小；当x≥-3时，y随x的增大而增大；当x=-3时，y有最小值为5;(1)说出函数的图象可以由y=ax2如何平移得到？21112yx－5.5－1.5－5.5－3(2)说出函数的图象如何平移可以得到y=ax2的图像？二、顶点式与平移21112yx21112yx(3)说出函数的图象如何平移可以得到的图像？一般地，抛物线与形状______，位置不同，把抛物线y=ax2向上（下）向左（右）_______，可以得到抛物线平移的方向、距离要根据_________的值来决定．抛物线有如下特点：（1）当a>0时，开口______；当a<0时，开口_______；（2）对称轴是直线______；（3）顶点坐标是_________2yaxhk2yaxkhxay22yaxhk相同平移h，k向上向下x=h（h,k)怎样把函数y=3x2-6x+5的转化成y=a(x-h）2+k的形式?函数y=ax²+bx+c的图象配方:5632xxy35232xx提取二次项系数3511232xx配方:加上再减去一次项系数绝对值一半的平方32132x整理:前三项化为平方形式，后两项合并同类项.2132x化简:去掉中括号老师提示:配方后的表达式通常称为顶点式简单说成：一提、二配、三化简函数y=3x2-6x+5的图象特征2.根据配方式(顶点式)确定开口方向,对称轴,顶点坐标.∵a=3>0,∴开口向上;对称轴:直线x=1;顶点坐标:(1,2)..2132xy例.求次函数y=ax²+bx+c的对称轴和顶点坐标．函数y=ax²+bx+c的顶点式配方:cbxaxy2ccxabxa2提取二次项系数acababxabxa22222配方:加上再减去一次项系数绝对值一半的平方222442abacabxa整理:前三项化为平方形式，后两项合并同类项.44222abacabxa化简:去掉中括号.44222abacabxay∴224.24bacbyaxaa顶点式：2yaxbxc一般式：可化为abx2它的对称轴是直线）它的顶点坐标（abaca44,2b-2三、把一般式化为顶点式1.x2-6x+=(x-)22.y2+3y+=(y+)23.函数y=x2+6x化为顶点式是。4.函数y=2x2-6x+9化为顶点式是。5.函数y=ax2+bx+c化为顶点式是.323223）（239)3(y2x29)23(22xy根据公式确定下列二次函数图象的对称轴和顶点坐标：21231;yxx222;yxx23=2441=-48baacba解：∵∴对称轴顶点坐标34x31(,)48解：∵212414baacba∴对称轴x=1顶点坐标(1,1)四、利用顶点式求二次函数解析式1.已知抛物线y=ax2+bx+c与y=-2x2的形状和开口方向相同，顶点为（-１，３），则它的函数解析式为.2.已知抛物线y=ax2+bx+c与y=-2x2的形状相同，顶点为（-１，３），则它的函数解析式为.3.已知抛物线y=ax2+bx+c由y=-2x2向左平移1个单位，再向上平移3个单位得到，则它的函数解析式为.4.已知抛物线y=ax2+bx+c由y=-2x2+1绕顶点旋转1800得到，则它的函数解析式为.5.已知抛物线y=ax2+bx+c与y=-2x2+1关于x轴对称，则它的函数解析式为.1422xxy1422xxy或542y2xx1423)1(2y22xxyx即122xy12y2x6.要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管应多长？解：如图建立直角坐标系，点（1，3）是图中这段抛物线的顶点，因此可设这段抛物线对应的函数是y=a(x－1)2＋3(0≤x≤3).由这段抛物线经过点（3，0）可得0＝a(3－1)2＋3.解得因此当x=0时，y=2.25，也就是说，水管应长2.25m.43a3031432xxy1212331、y=3x2的图象向平移个单位，再向平移个单位，就得到函数y=3(x+2)2-5的图象。左2下52、抛物线y=-3(x+2)2-4的顶点在第象限。二五、课内练习3、将抛物线y=2(x-1)2+4绕着它的顶点旋转180°，则旋转后的抛物线的解析式为（）A、y=2(x+1)2+4B、y=2(x-1)2-4C、y=-2(x-1)2+4D、y=-2(x+1)2+4C4.写出一个二次函数的解析式,要求满足下列条件:①开口向下;②顶点坐标为(-2,-3)..5.已知一抛物线的顶点坐标为(-1,2),且过点(1,-2),求该抛物线的解析式.6.已知抛物线(1)将函数化为的形式.(2)说出该函数图象可由抛物线如何平移得到?(3)说出该函数的对称轴,顶点坐标,最值情况.562xxykmxay2)(2xy3)2(2xy5、解：设抛物线的解析式为，将（1，-2）代入中，得：4a+2=-2a=-1则抛物线的解析式为2)1(y2xa2)1(y2xa2)1(2xyB1.抛物线y=2x2+8x-11的顶点在（）A.第一象限B.第二象限C.第三象限D.第四象限2.不论k取任何实数，抛物线y=a(x+k)2+k(a≠0)的顶点都在A.直线y=x上B.直线y=-x上C.x轴上D.y轴上3.若二次函数y=ax2+4x+a-1的最小值是2,则a的值是•4B.-1C.3D.4或-14.若二次函数y=ax2+bx+c的图象如下,与x轴的一个交点为(1,0),则下列各式中不成立的是()A.b2-4ac>0B.abc>01CAxyo-1B()（）5.若把抛物线y=x2+bx+c向左平移2个单位,再向上平移3个单位,得抛物线y=x2-2x+1,则A.b=2B.b=-6,c=6C.b=-8D.b=-8,c=186.若一次函数y=ax+b的图象经过第二、三、四象限，则二次函数y=ax2+bx-3的大致图象是()()BxyoxyoxyoxyoABCD-3-3-3-3C7.在同一直角坐标系中,二次函数y=ax2+bx+c与一次函数y=ax+c的大致图象可能是（）CxyoxyoxyoxyoABCD抛物线位置与系数a，b，c的关系：⑴a决定抛物线的开口方向：a＞0开口向上a＜0开口向下⑵a，b决定抛物线对称轴的位置:(对称轴是直线x=－—)①a，b同号对称轴在y轴左侧；②b=0对称轴是y轴；③a，b异号对称轴在y轴右侧2ab【左同右异】知识点一：⑶c决定抛物线与y轴交点的位置：①c＞0↔图象与y轴交点在x轴上②c=0↔图象过原点；③c＜0↔图象与y轴交点在x轴下方。⑷顶点坐标是（，）。ab2abac442（5）二次函数有最大或最小值由a决定。当x=－—时,y有最大(最小)值b2a______________________4a4ac－b2△（b2-4ac）的符号：由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<0（6）1、抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：xyoa>0,b<0,c>0,△>0.练习2、抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：xyoa>0,b>0,c=0,△>0.练习3、抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：xyoa<0,b<0,c>0,△>0.练习4、抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：xyoa>0,b=0,c>0,△=0.练习5、抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：xyoa>0,b=0,c=0,△=0.练习6、抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：xyoa<0,b>0,c<0,△<0.练习7、已知：二次函数y=ax2+bx+c的图象如图所示，则点M（，a）在（）A、第一象限B、第二象限C、第三象限D、第四象限cbxoya<0,b>0,c>0,D练习8、已知：一次函数y=ax+c与二次函数y=ax2+bx+c，它们在同一坐标系中的大致图象是图中的（）xyoxyoxyoxyo（A）（B）（C）（D）C练习9、已知：二次函数y=ax2+bx+c的图象如图所示，下列结论中：①abc＞0；②b=2a；③a+b+c＜0；④a+b-c＞0;a-b+c⑤＞0正确的个数是（）A、2个B、3个C、4个D、5个xoy-11C练习知识点二：抛物线y=ax2+bx+c的符号问题：（7）a+b+c的符号：由x=1时抛物线上的点的位置确定点在x轴上方点在x轴下方点在x轴上a+b+c>0a+b+c<0a+b+c=0（8）a-b+c的符号：由x=-1时抛物线上的点的位置确定点在x轴上方点在x轴下方点在x轴上a-b+c>0a-b+c<0a-b+c=011、已知：二次函数y=ax2+bx+c的图象如图所示，下列结论中下不正确的是（）A、abc＞0B、b2-4ac＞0C、2a+b＞0D、4a-2b+c＜0xoy-11D练习试一试：已知;二次函数y=2x2-(m+1)x+(m-1).(1)求证:不论m为何值时,函数的图像与x轴总有交点,并指出m为何值时,只有一个交点；(2)当m为何值时,函数图像过原点,并指出此时函数图像与x轴的另一个交点；(3)若函数图像的顶点在第四象限,求m的取值范围.(2)另一个交点坐标为(1，0)(3)当m＞-1且m≠3时,抛物线的顶点在第四象限.30.0,)3()1(24)1()1(22轴只有一个交点抛物线与时，＝时，即＝轴总有交点，且当抛物线与为何值时，无论xmxmmmm抛物线y=ax2+bx+c的符号问题：（1）a的符号：由抛物线的开口方向确定（2）C的符号：由抛物线与y轴的交点位置确定（4）b2-4ac的符号：由抛物线与x轴的交点个数确定（3）b的符号：由对称轴的位置与a确定（5）a+b+c的符号：由x=1时抛物线上的点的位置确定（6）a-b+c的符号：由x=-1时抛物线上的点的位置确定（7）2a±b的符号：对称轴与直线x=1或x=-1的位置确定小结4.若二次函数y=ax2+bx+c的图象如下,与x轴的一个交点为(1,0),则下列各式中不成立的是（）A.b2-4ac>0B.<0C.a+b+c=0D.>01xyo-1B-2ab4a4ac-b25.若二次函数y=ax2+bx+c的图象如下,与x轴的一个交点为(1,0),则下列各式中不成立的是()A.b2-4ac>0B.abc>0C.a+b+c=0D.a-b+c<0xyo1-1B6.若一次函数y=ax+b的图象经过第二、三、四象限，则二次函数y=ax2+bx-3的大致图象是()7.在同一直角坐标系中,二次函数y=ax2+bx+c与一次函数y=ax+c的大致图象可能是（）xyoxyoxyoxyoABCD-3-3-3-3xyoxyoxyoxyoABCDCC