用尺规作线段与角-2022-2023学年七年级数学上册同步精品课件(沪科版)

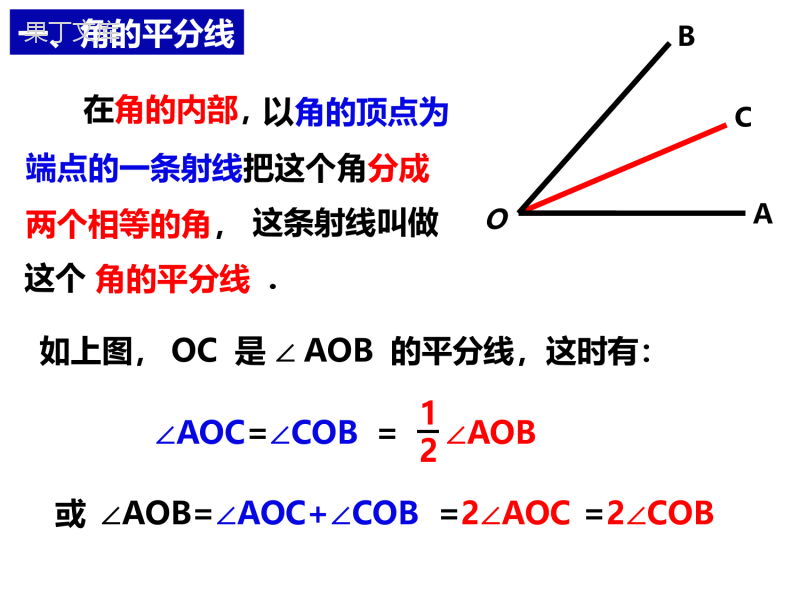
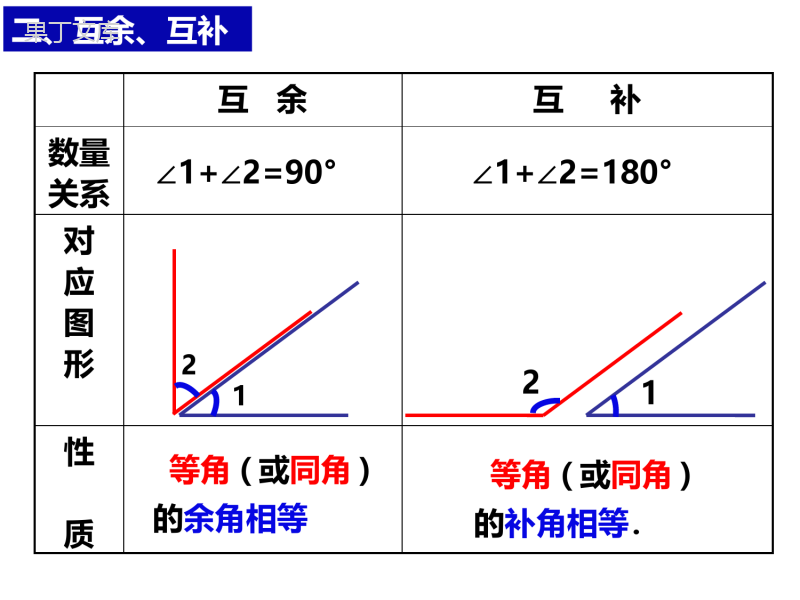
4.6用尺规作线段与角一、角的平分线ACBO这条射线叫做这个.以角的顶点为端点的一条射线把这个角分成两个相等的角，在角的内部，角的平分线如上图，OC是∠AOB的平分线，这时有：∠AOC=∠COB=∠AOB12或∠AOB=∠AOC+∠COB=2∠AOC=2∠COB∠1+∠2=90°∠1+∠2=180°互余互补数量关系对应图形性质等角(或同角)的余角相等等角(或同角)的补角相等．1221二、互余、互补情景引入请大家看看这些图形，它们是由哪些简单图形组成的？你能画出这些图形吗？在小学，我们已经会用刻度尺、三角尺、量角器和圆规等工具准确地画出线段、直线、射线、角、三角形等各种几何图形.画图形、设计图案，时常要画画一条线段等于已知线段，画一个角等于已知角，探究新知线段和角.可以先用刻度尺量出已知线段的长度，再画出等于这个长度的线段.可以先用量角器量出已知角的度数，再画出等于这个度数的角.探究新知想一想：如果你只有一个圆规和一把没有刻度的直尺，你能画出这些图案吗？探究新知想一想：如果你只有一个圆规和一把没有刻度的直尺，你能画出这些图案吗？尺规作图几何中，通常用没有刻度的直尺和圆规来画图，这种画图的方法叫做.下面介绍两种基本作图：①用尺规作一条线段等于已知线段；②用尺规作一个角等于已知角.求作：线段AB，使AB＝a.例1作一条线段等于已知线段.已知：线段a．作法：a①作射线AC;②以点A为圆心，以线段a的长度为半径画弧，交射线AC于点B.则线段AB即为所求线段.对应练习如图所示，已知线段a，b，c.求作：线段AD，使得AD=2a+b-c.ab作法：(1)①作射线AM;②在射线AM上依次截取AB=BC=a，CE=b，则线段AD就是所求作的线段.并在线段EA上截取ED=c.c想一想：如果没有三角尺和量角器，只用尺规作图能画出一个角等于已知角吗？探究新知探究新知已知：∠AOB.求作：∠DEF，使∠DEF＝∠AOB.例2作一个角等于已知角.①作射线EG;②以点O为圆心，③以点E为圆心，④以点D为圆心，⑤过点F作射线EF.则∠DEF即为所求的角.交OB于点Q;任意长为半径画弧，交OA于点P，交EG于点D;OP长为半径画弧，交前面所画弧于点F;PQ长为半径画弧，作法：BAO对应练习1、如图，已知∠α，∠β，且∠α＞∠β，用直尺和圆规作∠AOB，使得：(1)∠AOB=∠α+∠β(2)∠AOB=∠α-∠β(1)①作∠AOC=∠α;②在∠AOC的外部作则∠AOB即为所求的角.∠COB=∠β，作法：αβ对应练习1、如图，已知∠α，∠β，且∠α＞∠β，用直尺和圆规作∠AOB，使得：(1)∠AOB=∠α+∠β(2)∠AOB=∠α-∠β(2)①作∠AOC=∠α;②在∠AOC的内部作则∠AOB即为所求的角.∠COB=∠β，作法：αβ对应练习2、如图，已知∠α，用尺规作∠AOB=2∠α.α①作∠AOC=∠α;②在∠AOC的外部作则∠AOB即为所求的角.∠COB=∠α，作法：巩固练习1、用直尺和圆规按下列步骤作图：(1)作线段AB；(2)以点A为圆心，AB为半径画弧；(3)以点B为圆心，AB为半径画弧，与第(2)步所画的弧在AB的一方交于点C；(2)连接AC，BC，所得的是什么图形？2、已知线段a，b(a>b)，用直尺和圆规作一条线段AB，使得线段AB等于2a-b.ab巩固练习作法：(1)①作射线AM;②在射线AM上依次截取AB=BC=a，则线段AD就是所求作的线段.并在线段CA上截取CD=b.巩固练习3、如图，已知∠α，∠β.求作：∠AOB，使得∠AOB=2∠α-∠β.αβ1、尺规作图：不带刻度的直尺和圆规2、基本作图：①画一条线段等于已知线段;②画一个角等于已知角.3、作已知线段、角的和、差、倍数.