数据的离散程度(第1课时)-2022-2023学年八年级数学上册同步教材教学精品课件(北师大版)

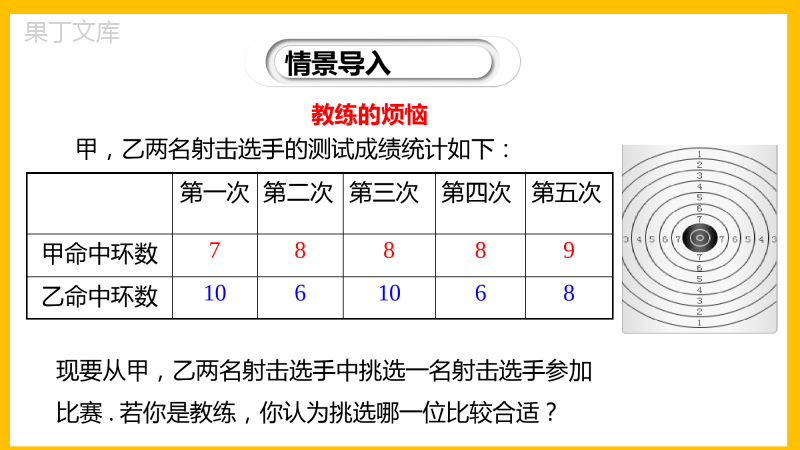
第六章数据的分析6.4.1数据的离散程度（第1课时）北师版数学八年级上册学习目标1．经历用方差刻画数据离散程度的过程，发展数据分析观念.2．了解刻画数据离散程度的三个量——极差、方差和标准差，能借助计算器求出相应的数值，并在具体问题情景中加以应用.情景导入数据特征众数平均数中位数数据分析折线统计图条形统计图扇形统计图集中趋势情景导入现要从甲，乙两名射击选手中挑选一名射击选手参加比赛.若你是教练，你认为挑选哪一位比较合适？教练的烦恼甲，乙两名射击选手的测试成绩统计如下：第一次第二次第三次第四次第五次甲命中环数78889乙命中环数1061068探索新知极差、方差与标准差一为了提高农副产品的国际竞争力，一些行业协会对农副产品的规格进行了划分，某外贸公司要出口一批规格为75g的鸡腿．现有2个厂家提供货源，它们的价格相同，鸡腿的品质也相近．质检员分别从甲、乙两厂的产品中抽样调查了20只鸡腿，它们的质量(单位:g)如下：甲厂：7574747673767577777474757576737673787772乙厂：7578727774757379727580717677737871767375探索新知7172737475767778790510152025甲厂707274767880820510152025乙厂(1)你能从图中估计出甲、乙两厂被抽取的鸡腿的平均质量吗？(2)在图中画出表示平均质量的直线.解：(1)甲、乙两厂被抽取鸡腿的平均质量大约是75g；(2)直线如图所示.7172737475767778790510152025甲厂707274767880820510152025乙厂探索新知(3)从甲厂抽取的这20只鸡腿质量的最大值是多少？最小值又是多少？它们相差几克？乙厂呢？(4)如果只考虑鸡腿的规格，你认为外贸公司应购买哪个厂家的鸡腿？解：甲厂：最大值78g，最小值72g，相差6g；乙厂：最大值80g，最小值71g，相差9g；解：平均质量只能反映总体的集中趋势,并不能反映个体的变化情况.从图中看,甲厂的产品更符合要求.总结归纳探索新知实际生活中，除了关心数据的集中趋势外，人们往往还关注数据的离散程度，即它们相对于集中趋势的偏离情况.一组数据中最大数据与最小数据的差（称为极差），就是刻画数据离散程度的一个统计量.极差=最大数-最小数探索新知如果丙厂也参与了竞争，从该厂也抽查20只鸡腿，717273747576777879800510152025丙厂（1）丙厂这20只鸡腿质量的平均数和极差分别是多少？平均数:75()xg丙极差:79727()g717273747576777879800510152025丙厂75()xg丙79727()g探索新知(2)如何刻画丙厂这20只鸡腿质量与其平均数的差距？分别求出甲、丙两厂的20只鸡腿质量与其平均数的差距.(2)可分别用这20只鸡腿的质量与其平均数差的绝对值刻画：甲厂的差距依次是：0,1,1,1,2,1,0,2,2,1,1,0,0,1,2,1,2,3,2,3.丙厂的差距依次：0.1,1.1,2.1,2.9,3.1,0.9,1.1,0.9,1.1,0.1,1.1,3.1,2.1,3.1,2.9,0.9,1.9,1.9,1.9,3.9,探索新知数学上，数据的离散程度还可以用方差或标准差刻画.方差是各个数据与平均数差的平方的平均数，即2222121nsxxxxxxn其中，x是x1，x2，……，xn的平均数，s2是方差，而标准差就是方差的算术平方根.一般而言，一组数据的极差、方差或标准差越小，这组数据就越稳定.总结归纳2222121nsxxxxxxn探索新知思考：（1）分别计算出从甲、丙两厂抽取的20只鸡腿质量的方差？（2）根据计算的结果，你认为哪家的产品更符合规格？解：（1）甲厂:[（75-75)2+…（72-75)2]÷20=2.5；丙厂:[（75-75.1)2+…（79-75.1)2]÷20=4.39.（2）根据计算结果，甲厂的方差小，表示甲厂鸡腿质量更稳定，产品更符合规格.探索新知甲团163164164165165166166167乙团163165165166166167168168哪个芭蕾舞团女演员的身高更整齐？例：在一次芭蕾舞比赛中，甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》，参加表演的女演员的身高（单位：cm）分别是：探索新知.22员的身高更整齐可知，甲芭蕾舞团女演由乙甲ss解:甲、乙两团演员的平均身高分别是方法一：2222(163165)(164165)...(167165)1.5,8甲S2222163-166165-166...168-1662.5.8乙（）（）（）S163164216521662167165,8甲x163165216621682167166.8乙x方差分别是2222(163165)(164165)...(167165)1.5,8甲S2222163-166165-166...168-1662.5.8乙（）（）（）S163164216521662167165,8甲x163165216621682167166.8乙x探索新知方法二：解:取a=165甲芭蕾舞团数据为：-2，-1，-1，0，0，1，1，2乙芭蕾舞团数据为：-2，0，0，1，1，2，3，3求两组新数据方差.21.5S甲22.5S乙21.5S甲22.5S乙探索新知求一组较大数据的方差，有如下简便计算方法：1.任取一个基准数a；2.将原数据减去a，得到一组新数据；3.求新数据的方差.总结归纳当堂检测1．在－2，1，2，1，4，6中正确的是()A．平均数3B．众数是－2C．中位数是1D．极差为8D2．若一组数据－1，0，2，4，x的极差为7，则x的值是()A．－3B．6C．7D．6或－3D当堂检测3．一组数据10，10，9，8，x的平均数是9，则这组数据的极差是____．24．小明用s2＝110[(x1－3)2＋(x2－3)2＋…＋(x10－3)3]计算一组数据的方差，那么x1＋x2＋x3＋…＋x10＝______．304．小明用s2＝110[(x1－3)2＋(x2－3)2＋…＋(x10－3)3]计算一组数据的方差，那么x1＋x2＋x3＋…＋x10＝______．当堂检测5．为了比较甲、乙两种水稻秧苗谁出苗更整齐，每种秧苗各随机抽取50株，分别量出每株长度，发现两组秧苗的平均长度一样，甲、乙的方差分别是3.5，10.9，则下列说法正确的是()A．甲秧苗出苗更整齐B．乙秧苗出苗更整齐C．甲、乙出苗一样整齐D．无法确定甲、乙出苗谁更整齐A当堂检测6.为了响应学校“书香校园”建设，阳光班的同学们积极捐书，其中宏志学习小组的同学捐书册数分别是5，7，x，3，4，6.已知他们平均每人捐5本，则这组数据的众数、中位数和方差分别是()A．5，5，32B．5，5，10C．6，5.5，116D．5，5，53D6.为了响应学校“书香校园”建设，阳光班的同学们积极捐书，其中宏志学习小组的同学捐书册数分别是5，7，x，3，4，6.已知他们平均每人捐5本，则这组数据的众数、中位数和方差分别是()A．5，5，32B．5，5，10C．6，5.5，116D．5，5，53当堂检测7．省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表：(单位：环)(1)根据表格中的数据，计算出甲的平均成绩是____环，乙的平均成绩是____环；(2)分别计算甲、乙六次测试成绩的方差；99第一次第二次第三次第四次第五次第六次甲10898109乙107101098当堂检测(3)根据(1)(2)计算的结果，你认为推荐谁参加全国比赛更合适？请说明理由．解：(2)s甲2＝23，s乙2＝43(3)推荐甲参加比赛更合适，理由：两人的平均成绩相等，说明实力相当；但甲的六次测试成绩的方差比乙小，说明甲发挥较为稳定，故推荐甲参加比赛更合适(3)根据(1)(2)计算的结果，你认为推荐谁参加全国比赛更合适？请说明理由．解：(2)s甲2＝23，s乙2＝43(3)推荐甲参加比赛更合适，理由：两人的平均成绩相等，说明实力相当；但甲的六次测试成绩的方差比乙小，说明甲发挥较为稳定，故推荐甲参加比赛更合适1．方差是用来衡量一组数据波动大小的重要统计量，反映的是数据在平均数附近波动的情况，对于同类问题的两组数据，方差越大，数据波动就越大，方差越小，数据波动就越小；在统计中常用样本方差去估计总体方差．2．极差是一组数据中的最大数据与最小数据的差．极差能反映数据的变化范围，是最简单的度量数据波动的量．3.标准差就是方差的算术平方根.