二次函数字母系数与图象的关系(课件)-2022-2023学年九年级数学上册同步精品课堂(人教版)

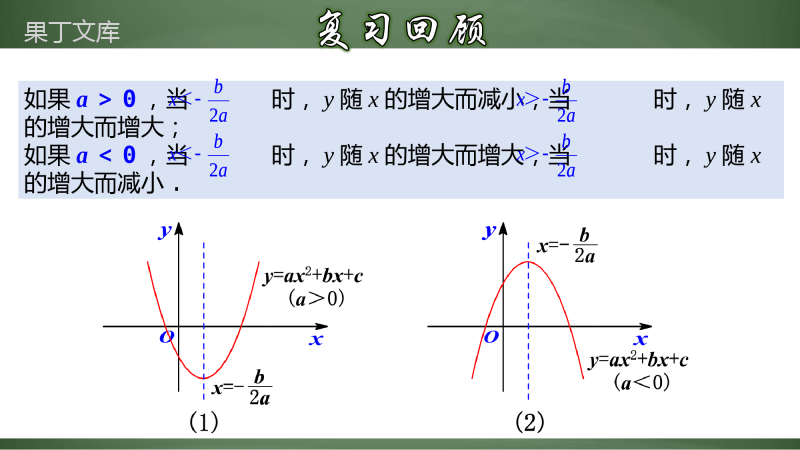
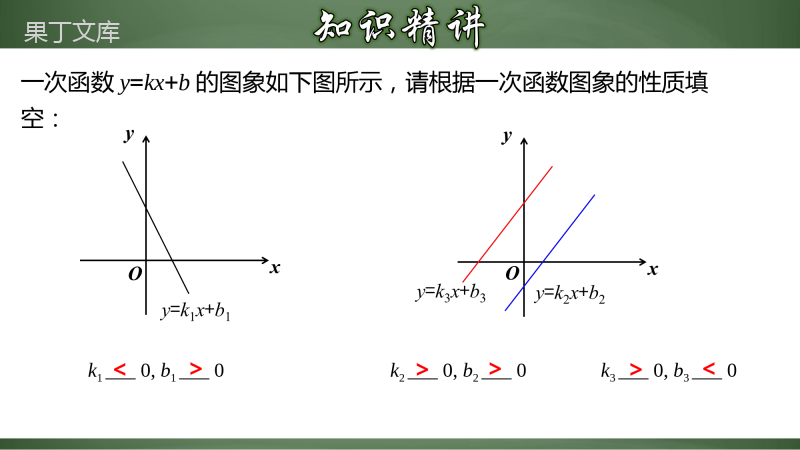
二次函数字母系数与图象的关系1.理解并掌握二次函数字母系数与图象的关系.(难点）2.能灵活利用二次函数字母系数与图象的关系解决相关问题.（重点）配方2yaxbxc22424bacbyaxaa对称轴是直线，顶点是.如果a＞0时，那么当时，y最小值=；如果a＜0时，那么当时，y最大值=.2bxa242bacbaa，42bxa2bxa24acba424acba42yaxbxc22424bacbyaxaa2bxa242bacbaa，42bxa2bxa24acba424acba4如果a＞0，当时，y随x的增大而减小，当时，y随x的增大而增大；如果a＜0，当时，y随x的增大而增大，当时，y随x的增大而减小.2bxa＜2bxa＞2bxa＜2bxa＞2bxa＜2bxa＞2bxa＜2bxa＞一次函数y=kx+b的图象如下图所示，请根据一次函数图象的性质填空：k1___0,b1___0k2___0,b2___0＞＞＜＞k3___0,b3___0＜＞xyO222bxa112bxa二次函数的图象如下图所示，请根据二次函数的性质填空：2yaxbxca1___0b1___0c1___0a2___0b2___0c2___0＞＞＞＞＜＝开口向上，a＞0对称轴在y轴左侧，x＜0对称轴在y轴右侧，x1102bxa＜2202bxa＞x=0时，y=c.222bxa112bxa2yaxbxc1102bxa＜2202bxa＞xyO442bxa332bxaa3___0b3___0c3___0a4___0b4___0c4___0＜＝＞＜＞＜开口向下，a＜0对称轴是y轴，x=0对称轴在y轴右侧，x33=02bxa4402bxa＞x=0时，y=c.二次函数的图象如下图所示，请根据二次函数的性质填空：2yaxbxc442bxa332bxa33=02bxa4402bxa＞2yaxbxc二次函数y=ax2+bx+c的图象与a、b、c的关系向上向下y左右正负例1.在同一坐标系中一次函数y=ax-b和二次函数y=ax2+bx+c的图象可能为（）【分析】解：A.由抛物线可知，，，得，由直线可知，，，故本选项错误；B．由抛物线可知，，由直线可知，，故本选项错误；C．由抛物线可知，，，得，由直线可知，，，故本选项正确；D．由抛物线可知，，由直线可知，，故本选项错误．故选：C．C在同一平面直角坐标系中，函数y=ax2+bx(a≠0)与y=ax+b的图象可能是（）A解：函数经过原点（0，0），则B错误；当a<0时，经过二、四象限，则D错误；当时，b>0，经过一、二、四象限，则C错误；当a>0，时，b<0，经过一、三、四象限，则A符合题意．故选：A．例2.如图，一次函数y1=x与二次函数y2=x2+bx+c的图像相交于P、Q两点，则函数y=x2+(b-1)x+c的图像可能是（）解：由=x2+bx+c图象可知，对称轴x=＞0，，，抛物线与y轴的交点在x轴下方，故选项B，C错误，抛物线的对称轴为，∴，∴抛物线y=x2+（b-1）x+c的对称轴在y轴的右侧，故选项D错误，故选：A．A例2.二次函数y=ax2+bx+c（a，b，c是常数，a≠0）的自变量x与函数值y的部分对应值如下表：且当时，其对应的函数值．有下列结论：①；②和3是关于x的方程的两个根；③对称轴为；④；其中，正确结论的个数是（）A．0B．1C．2D．3C【分析】利用待定系数法将点，代入解析式求出，，再结合二次函数图象与已知信息当时，得出，进而判断①结论；根据二次函数对称轴进而判断③结论；由二次函数的轴对称性进而判断②结论；利用待定系数法将点，代入解析式得出，再由判断④结论．已知二次函数（，，是常数，且）的自变量与函数值的部分对应值如下表：…012………当时，与其对应的函数值，给出下列四个结论：①；②关于的方程的两个根是和2；③；④（为任意实数．）其中正确结论的个数是（）A．1B．2C．3D．4C例3.如图，抛物线过点，且对称轴为直线，有下列结论①；②：③抛物线经过点与点，则；④无论a，b，c取何值，抛物线都经过同一个点；⑤，其中正确的结论是（）A．①②③B．③④⑤C．②③④D．②④⑤【分析】由开口方向、对称轴及抛物线与y轴交点位置可判断①；由x＝3时的函数值及a＞0可判断②；由抛物线的增减性可判断③；由当x＝﹣时，，且ab+c﹣＝0可判断④；由x＝1时函数y取得最小值及b＝﹣2a可判断⑤．D二次函数y＝ax2＋bx＋c的图象如图所示，对称轴是直线x＝1，下列结论：①abc＞0；②2a＋b＜0；③ab﹣＋c＞0；④9a＋3b＋c＜0，其中正确的是（）A．①③④B．①②③C．①③D．②③【分析】由抛物线开口向上，得到a＞0，再由对称轴在y轴右侧，得到a，b异号，得到b＜0，由抛物线与y轴交于负半轴，得到c＜0，据此判断①正确；由对称轴为直线x＝1，利用对称轴公式得到b＝﹣2a，可判断②错误；根据图象可知，当x＝﹣1时，y＞0，，代入解析式解答，可判断③正确；由抛物线对称轴x＝1，且x＝3与x＝﹣1时函数值相等，求出当x＝﹣1时，对应的函数值小于0，可判断④错误．C例4．如图，二次函数y=ax2+bx+c的图象关于直线x=1对称，与x轴交于A(x1,0)，B(x2,0)两点，若-20，③b2>a+c+4ac，④a>c>b．正确结论的个数为（）A．1个B．2个C．3个D．4个【分析】根据二次函数的对称性，即可判断①；由开口方向和对称轴即可判断②；根据抛物线与x轴的交点已经x=-1时的函数的取值，即可判断③；根据抛物线的开口方向、对称轴，与y轴的交点以及a－b＋c＜0，即可判断④．B例5．如图，抛物线的对称轴是，并与x轴交于A，B两点，若，则下列结论中：①；②；③；④若m为任意实数，则，正确的个数是（）A．1B．2C．3D．4【分析】根据函数图像的开口方向，对称轴，图像与y轴的交点，即可判断①；根据对称轴x=-2，OA=5OB，可得OA=5，OB＝1，点A（－5，0），点B（1，0），当x＝1时，y＝0即可判断②；根据对称轴x=-2以及a+b+c=0得a与c的关系，即可判断③；根据函数的最小值是当x＝－2时y＝4a－2b＋c即可判断④.C例6．如图，已知抛物线的顶点是，与x轴交于点，给出以下结论：①；②；③若，则或；④．其中正确的结论个数是（）A．1B．2C．3D．4【分析】根据开口方向、对称轴，判断a、b的符号及数量关系，根据抛物线与y轴的交点判断c的符号，根据图象与轴交于和对称轴判断抛物线与x轴的另一个交点，则可判断x=2时y的正负，取x=1，x=-1时，函数的表达式，进行相关计算即可证明，，然后化简即可得出正确．C1．已知二次函数，其中、，则该函数的图象可能为（）C2．已知，在同一平面直角坐标系中，二次函数与一次函数的图象如图所示，则二次函数的图象可能是（）B3．已知二次函数的图象如图所示，有下列结论：①；②；③；④；⑤（，m为实数），其中正确的结论有（）个．A．2个B．3个C．4个D．5个B4．已知抛物线y=ax2+bx+c的对称轴为x=1，与x轴正半轴的交点为A（3，0），其部分图象如图所示，有下列结论：①abc>0；②2c﹣3b<0；③5a+b+2c=0；④若B（，y1）、C（，y2）、D（，y3）是抛物线上的三点，则y1