湘教版数学九年级上册-《正弦和余弦(第3课时)》习题课件4

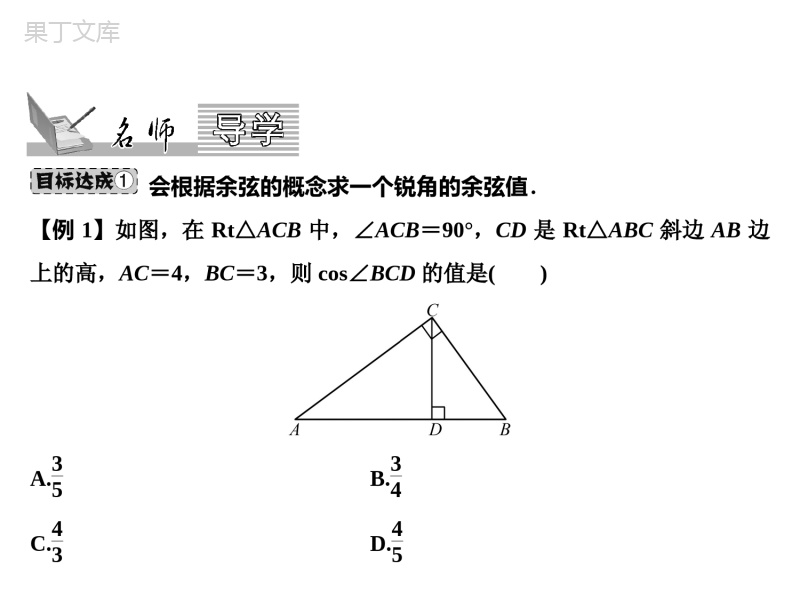
第4章锐角三角函数4.1正弦和余弦第3课时会根据余弦的概念求一个锐角的余弦值．【例1】如图，在Rt△ACB中，∠ACB＝90°，CD是Rt△ABC斜边AB边上的高，AC＝4，BC＝3，则cos∠BCD的值是()A.35B.34C.43D.45【思路分析】因为∠ACB＝90°，所以∠A＋∠B＝90°，因为CD⊥AB，所以∠B＋∠BCD＝90°，根据同角的余角相等，得∠A＝∠BCD，则cos∠BCD＝cosA，在Rt△ABC中，∠ACB＝90°，由勾股定理，得AB＝AC2＋BC2＝5，cosA＝ACAB＝45，所以可求出cos∠BCD.【规范解答】D【题后反思】当一个锐角的三角函数值不易求出时，常找到与它相等的角，求出等角的三角函数值使问题得到解决，体现了转化的思想方法．能熟记30°，45°，60°角的余弦值．【例2】根据下列条件求锐角α.2cos(30°＋α)－2＝0【思路分析】先把30°＋α看作一个整体，由cos(30°＋α)＝22，再根据特殊角的余弦值，得30°＋α＝45°，即可求出α.【规范解答】∵2cos(30°＋α)－2＝0∴cos(30°＋α)＝22∴α＋30°＝45°∴α＝15°1．Rt△ABC中，∠C＝90°，AC＝3，AB＝5，则cosA＝，cosB＝.2．α是120°角的补角，则cosα＝，cos(90°－α)＝.3．β是等腰直角三角形的底角，则cosβ＋sin(90°－β)＝.4．在Rt△ABC中，∠C＝90°，sinA＝34，则cosB＝.354512322345．在Rt△ABC中，∠C＝90°，BC＝5，AC＝12，则cosA等于()A.512B.513C.1213D.1256．点(sin60°，cos60°)关于y轴的对称点的坐标是()A．(32，12)B．(－32，12)C．(－32，－12)D．(－12，－32)CB7．如图，以圆O为圆心，半径为1的弧交坐标轴于A、B两点，P是上一点(不与A、B重合)，连接OP，设∠POB＝a，则点P的坐标是()A．(sina，sina)B．(cosa，cosa)C．(cosa，sina)D．(sina，cosa)8．在Rt△ABC中，∠C＝90°，若sinA＝513，则cosA的值为()A.512B.813C.23D.1213CD9．数字2，13，π，38，cos45°，0.32··中无理数的个数有()A．1B．2C．3D．410．cos55°与sin36°的大小关系是()A．cos55°＞sin36°B．cos55°＜sin36°C．cos55°＝sin36°D．无法确定CB11．在平面直角坐标系中，已知点A(2,1)和点B(3,0)，则cos∠AOB的值为()A.55B.255C.32D.1212．如图，在△ABC中，cosB＝22，sinC＝35，AC＝5，则△ABC的面积是()A.212B．12C．14D．21BA(第12题图)13．如图，在矩形ABCD中，DE⊥AC，∠ADE＝α，且cosα＝35，AB＝4，则AD的长为()(第13题图)A．3B.203C.163D.16514．在Rt△ABC中，∠C＝90°，AB＝13，cosB＝513，则AC＝.15．等腰三角形腰长10cm，高是8cm，则底角的余弦值是.16．在锐角△ABC中，∠A、∠B满足cosA－12＋sinB－222＝0，则∠C＝.C123575°17．计算：(1)(12)－1－2cos30°＋27＋(2－π)0解：原式＝3＋23(2)sin30°·cos60°＋cos45°·sin60°解：原式＝1＋64(3)sin213°＋sin277°－cos245°－2cos45°＋1－sin45°解：原式＝018．如图，矩形ABCD是供一辆机动车停放的车位示意图，请你参考图中数据，计算出停车位所占街道的宽度EF.(参考数据：sin40°≈0.64，cos40°≈0.77，结果精确到0.1m)解：在Rt△CDF中，CD＝5.4m，∠DCF＝40°，∴DF＝CD·sin40°≈5.4×0.64＝3.46(m)，在Rt△ADE中，AD＝2.2m，∠ADE＝∠DCF＝40°，∴DE＝AD·cos40°＝1.69(m)，∴EF＝DF＋DE≈5.15(m)≈5.2(m)，即停车位所占街道的宽度EF约为5.2m.19．阅读下面的材料，先完成阅读填空，再按要求答题：sin30°＝12，cos30°＝32，则sin230°＋cos230°＝；①sin45°＝22，cos45°＝22，则sin245°＋cos245°＝；②sin60°＝32，cos60°＝12，则sin260°＋cos260°＝；③…观察上述等式，猜想：对任意锐角A，都有sin2A＋cos2A＝.④1111(1)如图，在锐角三角形ABC中，利用三角函数的定义及勾股定理对∠A证明你的猜想；(2)已知∠A为锐角(cosA＞0)且sinA＝35，求cosA.解：(1)过点B作BH⊥AC于点H，则在Rt△ABH中，BH2＋AH2＝AB2，且sinA＝BHAB，cosA＝AHAB，∴sin2A＋cos2A＝BH2AB2＋AH2AB2＝BH2＋AH2AB2＝1(2)∵sin2A＋cos2A＝1，sinA＝35，∴cos2A＝1－(35)2＝1625，∵cosA＞0，∴cosA＝45