圆的对称性-2022-2023学年九年级数学下册教材配套教学课件(北师大版)

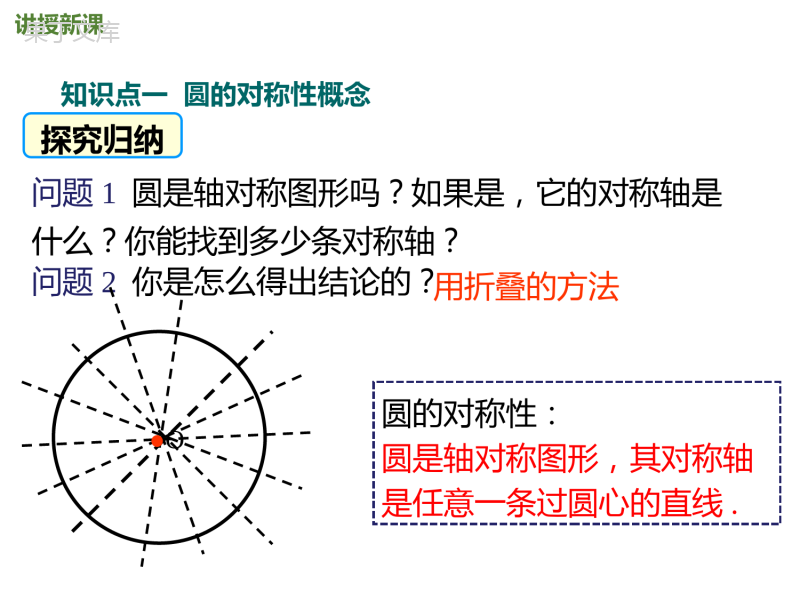
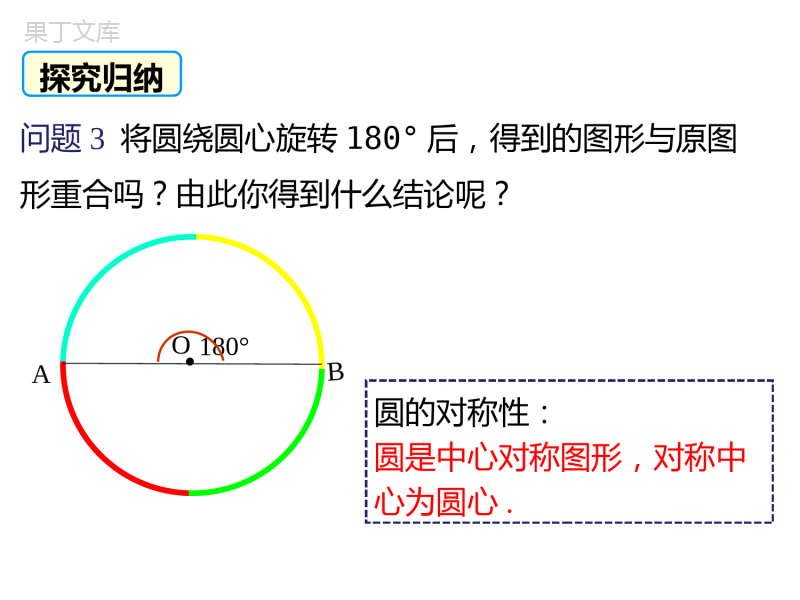
第三章圆3.2圆的对称性北师大版九年级下册新课导入讲授新课当堂检测课堂小结学习目标1、掌握圆的对称性，理解圆既是轴对称图形，也是中心对称图形；2、掌握圆心角、弧、弦之间关系定理并利用其解决相关问题.3、在理解相关的圆心角、弧、弦之间的关系时，记得一定要带上同圆或等圆这个条件；导入新课观察与思考观察图片，想一想，如何将一块蛋糕平均分成两块？四块？八块？分小组讨论一下；讲授新课知识点一圆的对称性概念问题1圆是轴对称图形吗？如果是，它的对称轴是什么？你能找到多少条对称轴？问题2你是怎么得出结论的？圆的对称性：圆是轴对称图形，其对称轴是任意一条过圆心的直线.用折叠的方法●O探究归纳.OAB180°问题3将圆绕圆心旋转180°后，得到的图形与原图形重合吗？由此你得到什么结论呢？探究归纳圆的对称性：圆是中心对称图形，对称中心为圆心.问题4把圆绕圆心旋转任意一个角度呢？仍与原来的圆重合吗？Oα圆是旋转对称图形，具有旋转不变性.·探究归纳知识点二圆心角、弧、弦之间的关系在同圆中探究在⊙O中，如果∠AOB=∠COD，那么，AB与CD，弦AB与弦CD有怎样的数量关系？⌒⌒C·OABD由圆的旋转不变性，我们发现：在⊙O中，如果∠AOB=∠COD，那么，，弦AB=弦CD归纳ABCDABCDO′·OAB如图，在等圆中，如果∠AOB＝∠CO′D，你发现的等量关系是否依然成立？为什么？·CD在等圆中探究通过平移和旋转将两个等圆变成同一个圆，我们发现：如果∠AOB=∠COD，那么，AB=CD，弦AB=弦CD.归纳⌒⌒在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．∠AOB=∠COD②AB=CD⌒⌒③AB=CDABODC要点归纳弧、弦与圆心角的关系定理想一想：定理“在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．”中，可否把条件“在同圆或等圆中”去掉？为什么？不可以，如图.ABODC在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．弧、弦与圆心角关系定理的推论要点归纳典例精析例1如图，AB，DE是⊙O的直径，C是⊙O上的一点，且AD=CE.BE和CE的大小有什么关系？为什么？·EBCOAD解:BE=CE.理由是：∵∠AOD=BOE∠，∴AD=BE.又∵AD=CE，∴BE=CE.∴BE=CE.⌒⌒⌒⌒⌒⌒⌒⌒证明：∴AB=AC．△ABC是等腰三角形.又∠ACB=60°，∴△ABC是等边三角形,AB=BC=CA.∴∠AOB＝∠BOC＝∠AOC.例2如图，在⊙O中，AB=AC,∠ACB=60°,求证：∠AOB=BOC=AOC.∠∠·ABCO⌒⌒温馨提示：本题告诉我们，弧、圆心角、弦灵活转化是解题的关键.∵AB=CD，⌒⌒当堂练习1．下列说法中，不正确的是（）A．过圆心的弦是圆的直径B．等弧的长度一定相等C．周长相等的两个圆是等圆D．直径是弦，半圆不是弧【答案】D【详解】A.直径是通过圆心且两个端点都在圆上的线段，故正确B.能重合的弧叫等弧，长度相等，故正确C.周长相等的圆其半径也相等，为等圆，故正确D.直径是弦，半圆是弧，故错误故选：D2．如图，已知AB是○O的直径，弧BC=弧CD=弧DE，∠BOC=40°，那么∠AOE=（）A．40°B．60°C．80°D．100°【答案】B【分析】先证明∠EOD=DOC=BOC=40°∠∠，∠BOE=3×40°=120°，再利用角的和差关系可得答案．【点睛】本题考查的是弧与圆心角之间的关系，掌握“弧，弦，圆心角的关系”是解本题的关键．3．如图，等腰三角形ABC的顶角∠BAC=36°，以腰AB为直径作圆，交BC于点D，交AC于点E，则弧DE的度数是（）A．18°B．36°C．72°D．80°【答案】B【详解】解：设圆心为O，连接OE、OD，∵AB=AC，∴∠ABC=ACB∠，∵OB=OD，∴∠OBD=ODB∠，∴∠ODB=ACB∠，∴ODAC∥，∴∠DOE=OEA∠，∵OA=OE，∴∠BAC=OEA∠，∴∠DOE=BAC=36°∠，即弧DE的度数为36°，故选：B．4．如图，AB是○O的直径，弧BC、弧CD与弧DE相等，∠COD=36°，则∠OEA的度数是（）A．30°B．36°C．54°D．72°【答案】C【分析】由弧BC、弧CD与弧DE相等，得∠COB=COD=∠∠EOD，即可求∠AOE．又因为OE和OA都是半径，长度相等，等边对等角，得∠OEA=AOE∠，根据三角形内角和180°就能求出∠OEA度数．5．在半径为1的圆中，长度等于的弦所对的弧的度数为____________．【答案】90°或270°【分析】根据勾股定理的逆定理可知，的弦与弦的端点两条长为1半径的围成的三角形是直角三角形．6．如图，AB是⊙O的直径，D.C是弧BE的三等分点，∠COD=32°，则∠E的度数是___________．【答案】48°【分析】先运用等弧对等角得出∠EOB=96°，再利用三角形外角性质即可求解．【详解】解：由C、D是BE的两个等分点，∠COD=32°知，∠BOC=DOE=COD=32°∠∠，∴∠EOB=96°，∵OE=OA，∴∠AEO=EAO=∠，故答案为：48°．7．如图，BC是○O的弦，AD过圆心O，且ADBC⊥．若∠COD=40°，则∠A的度数为______．【答案】20°【详解】解：连接OB，延长AD交圆于E，∵ADBC⊥，AD过圆心O，∴弧BE=弧CE，∴∠BOE=COD=40°∠，∴∠A=BOE=20°∠，故答案为：20°．8．如图，在○O中，弧AB=弧BC=弧CD，连接AC，CD，则AC__2CD（填“＞”，“＜”或“=”）．【答案】＜【点睛】本题考查了圆心角、弧、弦的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．也考查了三角形三边的关系．9．如图，已知AB是○O的直径，弦ACOD∥．(1)求证：弧BD=弧CD；(2)若弧AC的度数为58°，求∠AOD的度数．【答案】(1)见解析(2)119°【分析】（1）连接OC，根据等腰三角形的性质得出∠C=A∠，根据平行线的性质得出∠BOD=A∠，∠COD=C∠，求出∠COD=BOD∠，根据圆心角与弧的关系即可得证；（2）求出∠BOC，求出∠COD，再求出答案即可．10．如图，⊙O中，弦AB与CD相交于点E，AB=CD，连接AD、BC．求证：(1)AD=BC(2)AE=CE．【详解】（1）证明：∵AB=CD，∴弧AB=弧CD，∴弧AB-弧AC=弧CD-弧AC，∴弧AD=弧BC，∴AD=BC；（2）∵∠ADE=CBE∠，∠AED=CEB,AD=B∠C∴△ADECBE≌△（AAS），∴AE=EC．课堂小结圆是轴对称图形，其对称轴是任意一条过圆心的直线；圆是中心对称图形，对称中心为圆心.圆心角相等弧相等弦相等在同圆或等圆中