圆周角(2)课件2022-2023学年青岛版九年级数学上册

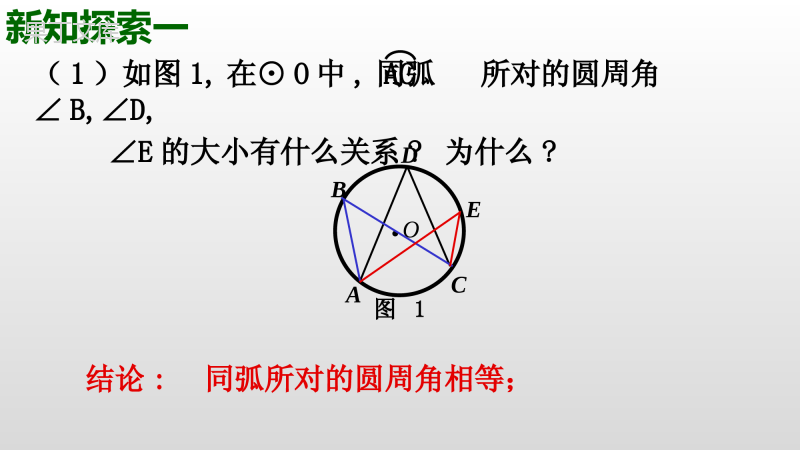
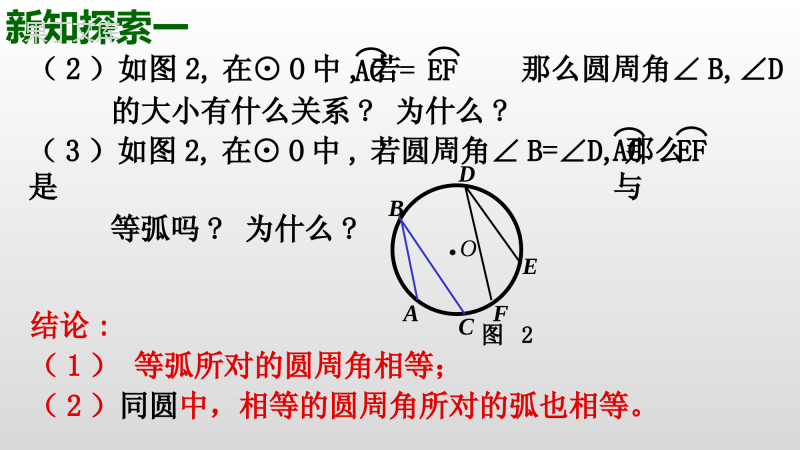
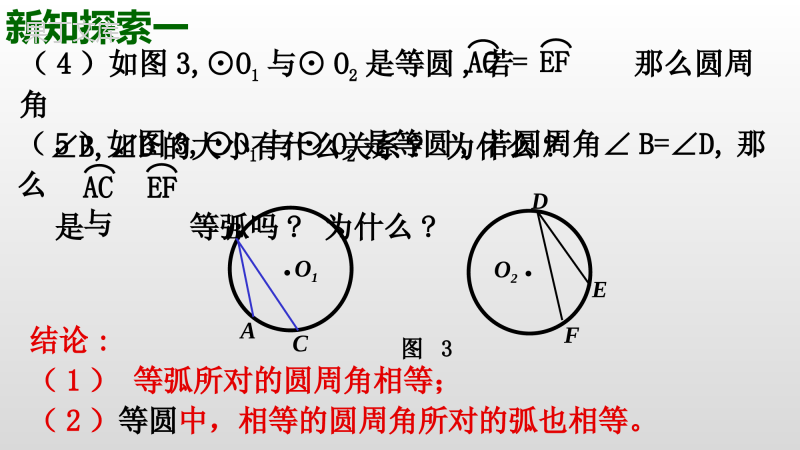
青岛版数学九（上）第3章：对圆的进一步认识3.3圆周角（2）复习回顾1、什么叫做圆周角?一条弧所对的圆周角等于它所对的圆心角的一半.2、圆周角定理：3、圆周角定理的推论1：圆周角的度数等于它所对弧的度数的一半.定义（1）：顶点在圆上,且角的两边分别与圆相交的角叫做圆周角.定义（2）：两条有公共端点的弦所夹的角叫做圆周角.新知探索一（1）如图1,在⊙O中,同弧所对的圆周角∠B,∠D,∠E的大小有什么关系?为什么?AC●OBACDE图1结论:同弧所对的圆周角相等；AC=EF（2）如图2,在⊙O中,若那么圆周角∠B,∠D的大小有什么关系?为什么?●OBACDEF图2新知探索一AC与EF（3）如图2,在⊙O中,若圆周角∠B=∠D,那么是等弧吗?为什么?结论:（1）等弧所对的圆周角相等；（2）同圆中，相等的圆周角所对的弧也相等。AC=EF（4）如图3,⊙O1与⊙O2是等圆,若那么圆周角∠B,∠D的大小有什么关系?为什么?新知探索一AC与EF（5）如图3,⊙O1与⊙O2是等圆,若圆周角∠B=∠D,那么是等弧吗?为什么?结论:（1）等弧所对的圆周角相等；（2）等圆中，相等的圆周角所对的弧也相等。●O1BAC图3O2●DEF新授知识小结11、圆周角定理的推论2（1）同弧或等弧所对的圆周角相等；（2）在同圆或等圆中，相等的圆周角所对的弧相等。●OBACDE图1●OBACDEF图2●O1BAC图3O2●DEF求:∠ACB的度数。已知:如图，AB是⊙O的任意一条直径，并在圆上任取一点C（不同A、B），连接AC、BC。●OCAB新知探索二解:∵AB是直径∴半圆AB的度数为180°的度数ABACB21∴∠ACB=90°还有其它解法吗？的度数ABACB21ACOB12解：连接OC.∴∠A=∠1,∠2=∠B.∴∠ACB=∠1+∠2=∠A+∠B∵∠ACB+∠A+∠B=180°∴2∠ACB=180°∴∠ACB=90°ACOB图2解：过点O作OD⊥BC于点D.D┓∵AB是⊙O的直径∴OA=OB=OC∵O是圆心∴点D是BC的中点∴OD是△ABC的中位线∴OD//AC∵OD⊥BC∴AC⊥BC∴∠ACB=90°2、圆周角定理的推论3：（1）半圆（或直径）所对的圆周角是直角.新授知识小结2你能说出该定理的逆命题吗？这个逆命题是真命题吗？（2）90°的圆周角所对的弦是直径.你能证明该逆定理吗？已知：A,B,C是⊙O上任一点,∠ACB=90°求证：AB是⊙O的直径.证明：取AB的中点O，并连接OC.∵△ABC是直角三角形，点O是AB的中点，∴OA=OB=OC∴O是△ABC的外接圆圆心∵AB是△ABC外接圆的弦，并且过圆心O∴弦AB是圆的直径ABC●O例题讲解例1、如图，△ABC内接与⊙O,A为劣弧的中点，∠BAC=120°,过点B作⊙O的直径BD，连接AD,若AD=6,求AC的长.BCACOBD解:点A是劣弧BC的中点∴AB=AC∴∠ABC=∠ACB∵∠BAC=120°∴∠ACB=120°∴∠D=∠ACB=120°∵BD是⊙O的直径∴∠DAB=90°在Rt△ABD中∵AD=6ADABDtan3230tan6AB32ABACADABDtan3230tan6AB32ABAC例2、如图，AB是⊙O的直径，D是圆上任意一点（不与A、B重合），连接BD并延长到C，使BD=DC,连接AC。试判断△ABC的形状。CD●OBA温馨提示：（1）有直径时，常常添加辅助线，构造直径所对的圆周角。例题讲解（2）有两个中点时，常常构造三角形的中位线。CD●OBACD●OBA理由：连接AD∴AB是⊙O的直径∴∠ADB=90°∴AD⊥BC∵BD=CD∴AD是BC的垂直平分线∴AB=AC解:△ABC是等腰三角形∴△ABC是等腰三角形解:△ABC是等腰三角形理由：连接OD∴OB=OD∴∠OBD=∠ODB∵O是AB的中点,BD=CD∴OD是△ABC的中位线∴OD//AC∴∠C=∠ODB∴∠OBD=∠C∴△ABC是等腰三角形ABCmDO●例3、如图,已知:△ABC内接于⊙O,AC=5,BC=12,AB=13,D是AmB的中点。求：BD的长。例题讲解提示：①△ABC是直角三角形吗？②弦AB是直径吗？③怎样把弦BD转化到直角三角形中？解：连接AD∵AC=5,BC=12,AB=13∴AC2+BC2=AB2∴∠ACB=90°∴AB是⊙O的直径∴∠ADB=90°∵点D是的中点AmBADBD∴=∴AD=BD∴∠DBA=∠DAB=45°ABCmDO●在Rt△ABD中ABBDDBAcos221345cos13BDABBDDBAcos221345cos13BD例4、如图，AD是△ABC的高，AE是△ABC的外接圆直径。求证：AB·AC=AE·AD提示：①AB·AC=AE·AD由什么式子变形得到？△ABD∽△AEC或△ABE∽△ADC例题讲解AOBCDE┓ACAEADABACADAEAB或可以由什么条件得到？或②ACAEADABACADAEAB③若得到两三角形相似，得作什么辅助线呢？ACAEADABACADAEAB或可以由什么条件得到？或②ACAEADABACADAEABAOBCDE┓证明：连接CE∵AE是⊙O的直径∴∠ACE=90°∴∠ADB=90°∵AD⊥BC∴∠ADB=∠ACE∵∠ABD=∠AEC(同弧所对的圆周角相等）∴△ABD∽△AECACADAEAB∴AB·AC=AE·ADACADAEABAOBCDE┓证明：连接BE∵AE是⊙O的直径∴∠ABE=90°∴∠ADC=90°∵AD⊥BC∴∠ABE=∠ADC∵∠AEB=∠ACD(同弧所对的圆周角相等）∴△ABE∽△ADCACAEADAB∴AB·AC=AE·ADACAEADAB例题讲解AOBCDE┓F例5、如图，AB是⊙O的直径,E为⊙O上一点,C是AE的中点，CD⊥AB垂足为D,AE交CD于F,连接AC。求证：AF=CF.提示：①因为AF,CF是△ACF的两边，若证AF=CF，得证哪两个角相等？∠FAC=∠FCA②∠FAC是圆周角，它所对的弧是CE，而AC所对的圆周角是哪一个呢？③怎样添加辅助④又怎样证∠ABC=∠FCA?AOBCDE┓F证明：连接BC∵AB是⊙O的直径∴∠ACB=90°∴∠ADC=90°∵CD⊥AB∴∠FCA=∠ABC∴∠ABC+∠DAC=90°∴∠FCA+∠DAC=90°∴AC=CE∵C是AE的中点∴∠FAC=∠ABC∴∠FCA=∠FAC∴AF=CF练习P87练习第1、2题3、如图，已知：OA是⊙O的半径，以OA为直径的⊙C与⊙O的弦AB相交于点D。求：AD与BD的关系，并说明理由。A●O●CDB温馨提示：有直径时，常常添加辅助线，构造直径所对的圆周角。练习AD=BD课堂小结1、圆周角定理的推论2：（1）同弧或等弧所对的圆周角相等；（2）在同圆或等圆中，相等的圆周角所对的弧相等。2、圆周角定理的推论3：（1）半圆（或直径）所对的圆周角是直角.（2）90°的圆周角所对的弦是直径.P89-90习题3.3第4、5、7题作业结束寄语●不学自知,不问自晓,●古今行事,未之有也.