专题2-2-二次函数的图象与性质(第5课时)-九年级数学下册教材配套教学课件(北师大版)

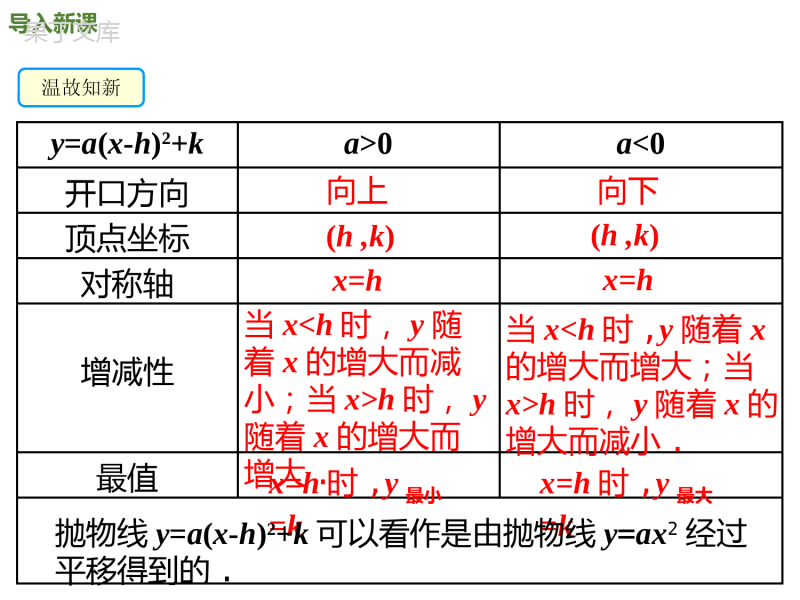
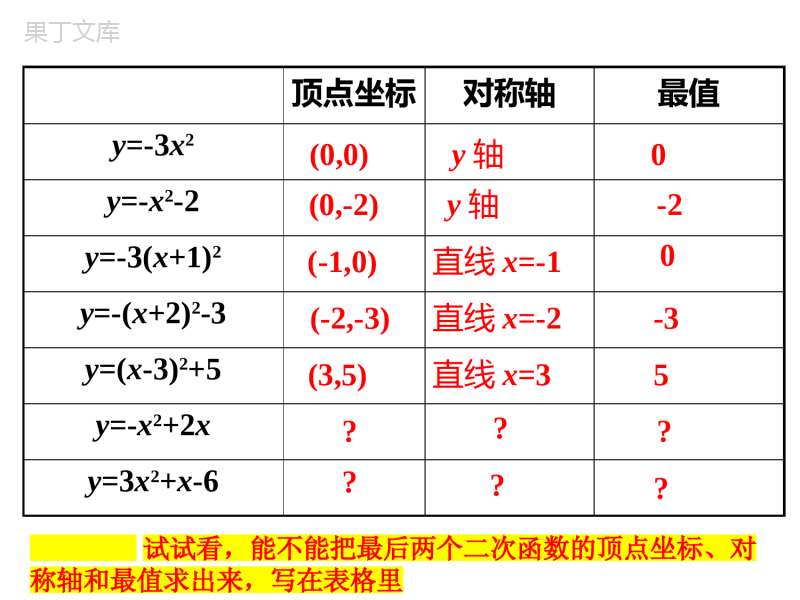
第二章二次函数2.2二次函数的图象与性质第5课时二次函数y=ax2+bx+c的图象与性质北师大版九年级下册新课导入讲授新课当堂检测课堂小结学习目标1、掌握用配方法或公式法将一般式y＝ax2＋bx＋c化成顶点式y=a(x-h)2+k.注意一般式转化为顶点式时a值的提取；2、将一般式转化为顶点式后，会熟练求出二次函数一般式y＝ax2＋bx＋c的顶点坐标、对称轴.3、灵活运用一般式，熟练掌握一般式的性质，注意要结合图象来研究；导入新课温故知新y=a(x-h)2+ka>0a<0开口方向顶点坐标对称轴增减性最值向上向下(h,k)(h,k)x=hx=h当xh时，y随着x的增大而增大.当xh时，y随着x的增大而减小.x=h时,y最小=kx=h时,y最大=k抛物线y=a(x-h)2+k可以看作是由抛物线y=ax2经过平移得到的.顶点坐标对称轴最值y=-3x2y=-x2-2y=-3(x+1)2y=-(x+2)2-3y=(x-3)2+5y=-x2+2xy=3x2+x-6(0,0)y轴0(0,-2)y轴-2(-1,0)直线x=-10(-2,-3)直线x=-2-3(3,5)直线x=35??????试试看，能不能把最后两个二次函数的顶点坐标、对称轴和最值求出来，写在表格里讲授新课知识点一二次函数y=ax2+bx+c的图象和性质合作探究我们已经知道y=a(x-h)2+k的图象和性质，能否利用这些知识来讨论的图象和性质？216212yxx问题1怎样将化成y=a(x-h)2+k的形式？216212yxx提示：采用配方法可以将该一般式化成y=a(x-h)2+k的形式216212yxx216212yxx216212yxx配方可得2221(126642)2xx21(1242)2xx2221[(126)642]2xx21[(6)6]2x21(6)3.2x熟悉左边的计算过程，总结一下，配方法将二次函数的一般式化成顶点式，需要注意什么？一般的步骤是什么？216212yxx2221(126642)2xx21(1242)2xx2221[(126)642]2xx21[(6)6]2x21(6)3.2x配方216212xxy你知道是怎样配方的吗？(1)“提”：提出二次项系数；(2)“配”：括号内配成完全平方；(3)“化”：化成顶点式.提示:配方后的表达式通常称为配方式或顶点式.3)6(212xy216212xxy3)6(212xy问题2你能说出的对称轴及顶点坐标吗？21(6)32yx答：对称轴是直线x=6,顶点坐标是（6，3）.问题3二次函数可以看作是由怎样平移得到的？21(6)32yx212yx答：平移方法1：先向上平移3个单位，再向右平移6个单位得到的；平移方法2：先向右平移6个单位，再向上平移3个单位得到的.21(6)32yx21(6)32yx212yx问题4如何用描点法画二次函数的图象？216212yxx…………9876543x解:先利用图形的对称性列表21(6)32yx7.553.533.557.5510xy510然后描点画图，得到图象如右图.O216212yxx21(6)32yx问题5结合二次函数的图象，说出其增减性.216212yxx510xy510x=6当x<6时，y随x的增大而减小；当x>6时，y随x的增大而增大.试一试你能用上面的方法讨论二次函数y=2x2-8x+7的图象和性质吗？O216212yxx要点归纳二次函数y=ax2+bx+c的图象和性质1.一般地，二次函数y=ax2+bx+c的可以通过配方化成y=a(x-h)2+k的形式，即2224().24bacbyaxbxcaxaa因此，抛物线y=ax2+bx+c的顶点坐标是：对称轴是：直线24(,).24bacbaa.2bxa2224().24bacbyaxbxcaxaa24(,).24bacbaa.2bxa(1)xyO如果a>0,当x<时，y随x的增大而减小；当x>时，y随x的增大而增大；当x=时，函数达到最小值，最小值为.2bxa2ba2ba2ba二次函数y=ax2+bx+c的图象和性质244acba(1)xyO如果a>0,当x<时，y随x的增大而减小；当x>时，y随x的增大而增大；当x=时，函数达到最小值，最小值为2bxa2ba2ba2ba244acba2bxa2ba2ba2ba244acba2bxa2ba2ba2ba244acba典例精析例1已知二次函数y=－x2＋4bx＋c，当x＞2时，y的值随x值的增大而减小，则实数b的取值范围是（）A．b≥－2B．b≤－2C．b≥2D．b≤2解析：∵二次项系数为－1＜0，∴抛物线开口向下，在对称轴右侧，y的值随x值的增大而减小，由题设可知，当x＞2时，y的值随x值的增大而减小，∴抛物线y=－x2＋4bx＋c的对称轴应在直线x=2的左侧而抛物线y=－x2＋4bx＋c的对称轴，即b≤2，422(1)bxbD422(1)bxb知识点二二次函数的系数与图象的关系合作探究问题1一次函数y=kx+b的图象如下图所示，请根据一次函数图象的性质填空：xyOy=k1x+b1xyOy=k2x+b2y=k3x+b3k1___0b1___0k2___0b2___0＜＞＞＜k3___0b3___0＞＞xyO222bxa112bxa问题2二次函数的图象如下图所示，请根据二次函数的性质填空：2yaxbxca1___0b1___0c1___0a2___0b2___0c2___0＞＞＞＞＜＝开口向上，a＞0对称轴在y轴左侧，对称轴在y轴右侧，1102bxa＜2202bxa＞x=0时，y=c.222bxa112bxa2yaxbxc1102bxa＜2202bxa＞xyO442bxa332bxaa3___0b3___0c3___0a4___0b4___0c4___0＜＝＞＜＞＜开口向下，a＜0对称轴是y轴，对称轴在y轴右侧，33=02bxa4402bxa＞x=0时，y=c.442bxa332bxa33=02bxa4402bxa＞例2已知二次函数y＝ax2＋bx＋c的图象如图所示，下列结论：①abc＞0；②2a－b＜0；③4a－2b＋c＜0；④(a＋c)2＜b2.其中正确的个数是()A．1B．2C．3D．4D由图象上横坐标为x＝－2的点在第三象限可得4a－2b＋c＜0，故③正确；由图象上x＝1的点在第四象限得a＋b＋c＜0，由图象上x＝－1的点在第二象限得出a－b＋c＞0，则(a＋b＋c)(a－【解析】由图象开口向下可得a＜0，由对称轴在y轴左侧可得b＜0，由图象与y轴交于正半轴可得c＞0，则abc＞0，故①正确；由对称轴x>－1可得2a－b＜0，故②正确；当堂练习1．抛物线y=-x2+4x+2的对称轴是直线（）A．x=-2B．x=2C．x=4D．x=-4【答案】B【分析】先将抛物线的解析式化成顶点式，即可由顶点式直接写出抛物线的对称轴．【详解】解：∵y=-x2+4x+2=-(x-2)2+6，∴抛物线y=-x2+4x+2的对称轴是直线x=2，故选：B．2．二次函数y=-x2+2x-4，当-1＜x＜2时，y的取值范围是（）A．-4＜y≤-3B．-7＜y＜-4C．-7≤y＜-3D．-7＜y≤-3【答案】D【分析】先把二次函数化为顶点式得到函数的最大值，再求解x=-1,x=2时的函数值，从而可得答案．【详解】解：∵二次函数y=-x2+2x-4=-(x-1)2-3，∴当x=1时，函数最大值为：-3，当x=-1时，y=-7，当x=2时，y=-4，∴当-1＜x＜2时，y的取值范围为：-7＜y≤-3，故选D．3．抛物线y=x2-2x-3向左平移三个单位、再向上平移两个单位，得到的抛物线的顶点坐标是（）A．(-4,-2)B．(-2,2)C．(-2,-2)D．(4,2)【答案】C【分析】根据抛物线的平移规律：上加下减，左加右减解答即可．【详解】解：抛物线y=x2-2x-3=(x-1)2-4向左平移三个单位、再向上平移两个单位，得到的抛物线为y=(x-1+3)2-4+2=(x+2)2-2，即y=(x+2)2-2，顶点坐标为(-2,-2)．故选C．4．关于x的二次函数y=x2-2mx+5，当x＞2时，y随x的增大而增大，则实数m的取值范围是（）A．m＜2B．m≤2C．m＞2D．m≥2【答案】B【分析】先求出二次函数的对称轴，再根据二次函数的性质解答即可．【详解】将二次函数y=x2-2mx+5化成顶点式为：y=(x-m)2+5-m2，二次函数y=x2-2mx+5的开口向上，对称轴是x=m，∵当x＞2时，y随x的增大而增大，∴2≥m，5．二次函数y=x2-2x-3的顶点坐标为_________，对称轴方程为__________．【答案】(1,-4)x=1【分析】先把抛物线化为顶点式y=x2-2x-3=(x-1)2-4，从而可得答案．【详解】解：∵y=x2-2x-3=(x-1)2-4，∴抛物线的顶点坐标为(1,-4)，对称轴为直线x=1．故答案为：(1,-4)，x=1．6．将二次函数y=-3x2+6x的图象绕顶点旋转180°所得抛物线解析式为_________．【答案】y=3x2-6x+6【详解】解：∵y=-3x2+6x=-3(x-1)2+3，∴原抛物线的顶点为(1,3)，由题意得：旋转后的图象和原图象关于顶点对称，开口方向相反，∴新图象的顶点为(1,3)，a=3，∴所得的图象的解析式为：y=3(x-1)2+3，即y=3x2-6x+6．故答案为：y=3x2-6x+6．7．已知二次函数y=-x2-2x+3，当-2≤x＜m时，函数值的取值范围是3≤x≤4，则m的取值范围是______．【答案】-1＜m≤0【分析】利用配方法将二次函数解析式由一般式变形为顶点式，代入x=0求出y的值，结合当-2≤x＜m时y的取值范围是3≤y≤4，即可得出m的值，验证后即可得出结论．【详解】解：∵y=-x2-2x+3=-(x+1)2+4，顶点坐标为(-1,4)，开口向下当x=-1时，取得最大值y=4，当x=0，y=3，根据对称性可得x=-2时，y=3∴-2≤x≤0时，函数值的取值范围是3≤y≤4，∵当-2≤x＜m时，函数值的取值范围是3≤y≤4，∴结合图象可得：-1＜m≤0，故答案为：-1＜m≤0．8．对于函数y=-x2+4x+3，当0≤x≤a时，y有最大值7，最小值3，则a的取值范围是________．【答案】2≤a≤4【详解】∵函数y=-x2+4x=3=-（x-2)2+7，∴开口向下，对称轴为型，顶点坐标为（2,7），最大值为7，∵当x=0时，y=3，∴根据二次函数对称性可得，当x=4时，y=3，∵0≤x≤a时，y有最大值7，最小值3，∴a的取值范围是2≤a≤4．故答案为：2≤a≤4．9．已知二次函数y=x2+2x-1(1)写出二次函数图像的开口方向、顶点坐标、对称轴；(2)在图中画出二次函数的图象；(3)当y=7时，求的值．【分析】（1）把抛物线解析式化为顶点式，即可求解；（2）列出表格，描点，连线，即可；（3）把y=7代入解析式，即可求解．【详解】（1）解：∵y=x2+2x-1=(x-1)2-2，∴抛物线开口向上，顶点坐标(-1,-2)，对称轴x=-1；（2）解：列表如下：x……-3-2-101……y……2-1-2-12……（3）解：当y=7时，x2+2x-1=7，解得：x=-4或x=2．10．抛物线y=-2x2+8x-6(1)用配方法求顶点坐标，对称轴；(2)x取何值时，y随x的增大而减小？(3)x取何值时，y＝0；x取何值时，y＞0；x取何值时，y＜0【答案】(1)顶点坐标为(2,2)，对称轴为直线x=2(2)当x≥2时，y随x的增大而减小(3)当x=1或x=3时，y=0，当1＜x＜3时，y＞0，当x＜1或x＞3时，y＜0【分析】（1）根据二次函数一般式化为顶点式的方法可进行求解；（2）由二次函数的性质可直接进行求解；（3）令y=0时代入二次函数解析式进行求解即可．【详解】（1）解：由y=-2x2+8x-6可知：y=-2(x2-4x)-6=-2(x-2)2+2，∴该二次函数的顶点坐标为(2,2)，对称轴为直线x=2；（2）解：由y=-2x2+8x-6可知：a=-2＜0，即开口向下，∴当x≥2时，y随x的增大而减小；（3）解：令y=0时，则-2x2+8x-6=0，解得：x1=1,x2=3，∴二次函数与x轴的交点坐标为(1,0),(3,0)，∴当1＜x＜3时，y＞0，当x＜1或x＞3时，y＜0．课堂小结24(,)24bacbaa2bxa顶点：对称轴：y=ax2+bx+c（a≠0)(一般式)配方法公式法(顶点式)224()24bacbyaxaa24(,)24bacbaa2bxa224()24bacbyaxaa