《全等三角形》-章节复习-2022-2023学年八年级数学上册教材配套教学课件(人教版)

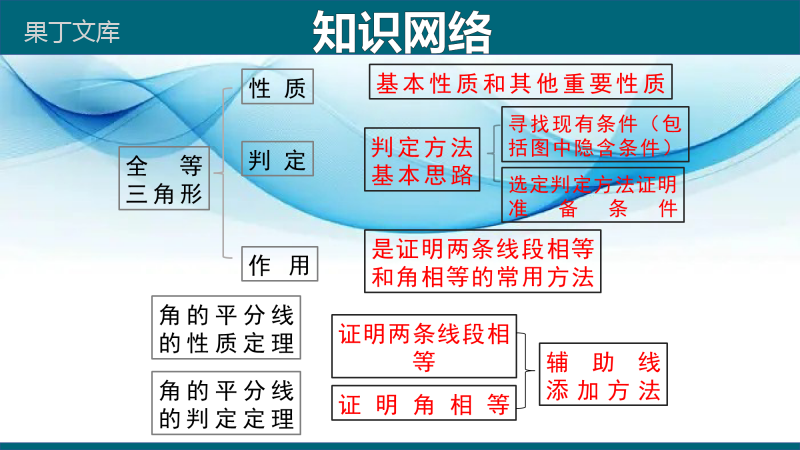
人教版数学八年级上册全等三角形章节复习人教版数学八年级下册学习目标1.通过知识梳理，使学生掌握三角形全等的概念、判定和性质。2.通过典型题的评析，提高学生的综合能力。3.培养逻辑思维能力，发展基本的创新意识和能力。学习重点和难点学习重点：掌握全等三角形的性质与判定方法。学习难点：对全等三角形性质及判定方法的运用。知识网络能够完全重合的两个图形叫全等图形，能够完全重合的两个三角形叫全等三角形。把两个全等的三角形重合到一起，重合的顶点叫做对应顶点，重合的边叫做对应边，重合的角叫做对应角。一、全等三角形的性质知识梳理BCEF△ABC≌DEF△其中点A和，点B和，点C和__是对应顶点.AB和，BC和，AC和是对应边.∠A和，∠B和，∠C和是对应角.AD点D点E点FDEEFDF∠D∠E∠F知识梳理ABCDEF性质：全等三角形的对应边相等，对应角相等.如图：∵△ABC≌△DEF，∴AB=DE，BC=EF，AC=DF（），∠A=∠D，∠B=∠E，∠C=∠F（）.全等三角形的对应边相等全等三角形的对应角相等几何语言：知识梳理用符号语言表达为：在△ABC与△DEF中∴△ABC≌△DEF.（SAS）1.两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).FEDCBAAC=DF，∠C=∠F，BC=EF，二、三角形全等的判定方法知识梳理∠A=∠D，（已知）AB=DE，（已知）∠B=∠E，（已知）在△ABC和△DEF中，∴△ABC≌△DEF.（ASA）2.有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”）.用符号语言表达为：FEDCBA知识梳理3.三边对应相等的两个三角形全等（可以简写为“边边边”或“SSS”）.ABCDEF在△ABC和△DEF中，∴△ABC≌△DEF.（SSS）AB=DE，BC=EF，CA=FD，用符号语言表达为：知识梳理4.有两角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”）.知识梳理FEDCBA用符号语言表达为：在△ABC和△DEF中，∠A=∠D，∠B=E∠，AC=DF，∴△ABC≌△DEF.（AAS）5.斜边和一条直角边对应相等的两个直角三角形全等.简写成“斜边、直角边”或“HL”.ABCDEF知识梳理注意：①对应相等.“②HL”仅适用直角三角形,③书写格式应为:在Rt△ABC和Rt△DEF中，AB=DE，AC=DF，∴Rt△ABC≌Rt△DEF(HL)【例1】如图，已知△ACE≌DBF△．CE=BF，AE=DF，AD=8，BC=2．（1）求AC的长度；（2）试说明CEBF∥．解：（1）∵△ACE≌DBF△，∴AC=BD，则AB=DC，∵BC=2，∴2AB+2=8，∴AB=3，∴AC=3+2=5；（2）∵△ACE≌DBF△，∴∠ECA=FBD∠，∴CEBF∥．全等三角形的性质1典型题解析【点睛】两个全等三角形的长边与长边，短边与短边分别是对应边，大角与大角，小角与小角分别是对应角.有对顶角的，两个对顶角一定为一对对应角.有公共边的，公共边一定是对应边.有公共角的，公共角一定是对应角.迁移应用1.如图所示，△ABD≌ACD△，∠BAC=90°．（1）求∠B；（2）判断AD与BC的位置关系，并说明理由．解：（1）∵△ABD≌ACD△，∴∠B=C∠，又∵∠BAC=90°，∴∠B=C=45°∠；（2）ADBC⊥．理由：∵△ABD≌ACD△，∴∠BDA=CDA∠，∵∠BDA+CDA=180°∠，∴∠BDA=CDA=90°∠，∴ADBC⊥．【例2】已知，∠ABC＝∠DCB，∠ACB＝∠DBC，求证：△ABC≌△DCB．∠ABC＝∠DCB(已知），BC＝CB（公共边），∠ACB＝∠DBC（已知），证明：在△ABC和△DCB中，△ABC≌△DCB（ASA）.BCAD【分析】运用“两角和它们的夹边对应相等两个三角形全等”进行判定．全等三角形的判定2典型题解析2.已知△ABC和△DEF,下列条件中,不能保证△ABC和△DEF全等的是()A.AB=DE,AC=DF,BC=EFB.∠A=∠D,∠B=∠E,AC=DFC.AB=DE,AC=DF,∠A=∠DD.AB=DE,BC=EF,∠C=∠FD迁移应用3.如图所示，AB与CD相交于点O，OA=OB添加条件，所以△AOC≌△BOD理由是.AODCB∠C=∠D或∠A=∠B或OC=ODAAS或ASA或SAS迁移应用【例3】如图，在△ABC中，AD平分∠BAC,CE⊥AD于点G,交AB于点E,EFBC∥交AC于点F,求证：∠DEC=∠FEC.ABCDFEG【分析】欲证∠DEC=∠FEC由平行线的性质转化为证明∠DEC=∠DCE只需要证明△DEG≌△DCG.全等三角形的性质与判定的综合应用3典型题解析ABCDFEG证明：∵CE⊥AD,∴∠AGE=∠AGC=90°.在△AGE和△AGC中，∠AGE=∠AGC，AG=AG，∠EAG=∠CAG，∴△AGE≌△AGC(ASA)，∴GE=GC.∵AD平分∠BAC,∴∠EAG=∠CAG，.考点解析ABCDFEG在△DGE和△DGC中，EG=CG，∠EGD=∠CGD=90°，DG=DG.∴△DGE≌△DGC(SAS).∴∠DEG=∠DCG.∵EF//BC,∴∠FEC=∠ECD，∴∠DEG=∠FEC.考点解析【点睛】利用全等三角形证明角相等，首先要找到两个角所在的两个三角形，看它们全等的条件够不够；有时会用到等角转换，等角转换的途径很多，如：余角，补角的性质、平行线的性质等，必要时要想到添加辅助线.4.如图，OB⊥AB,OC⊥AC,垂足为B,C,OB=OC，∠BAO=∠CAO吗？为什么？OCBA解：∠BAO=∠CAO，理由：∵OB⊥AB,OC⊥AC，∴∠B=∠C=90°.在Rt△ABO和Rt△ACO中，OB=OCAO=AO∴Rt△ABO≌Rt△ACO，（HL）∴∠BAO=∠CAO.迁移应用【例4】如图，两根长均为12米的绳子一端系在旗杆上，旗杆与地面垂直，另一端分别固定在地面上的木桩上，两根木桩离旗杆底部的距离相等吗？ABCD【分析】将本题中的实际问题转化为数学问题就是证明BD=CD.由已知条件可知AB=AC，AD⊥BC.利用全等三角形解决实际问题4考点解析ABCD解：相等，理由如下：∵AD⊥BC，∴∠ADB=∠ADC=90°.在Rt△ADB和Rt△ADC中，AD=AD，AB=AC，∴Rt△ADB≌Rt△ADC(HL).∴BD=CD.考点解析【点睛】利用全等三角形可以测量一些不易测量的距离和长度，还可对某些因素作出判断，一般采用以下步骤：（1）先明确实际问题；（2）根据实际抽象出几何图形；（3）经过分析，找出证明途径；（4）书写证明过程.5.如图，有一湖的湖岸在A、B之间呈一段圆弧状，A、B间的距离不能直接测得．你能用已学过的知识或方法设计测量方案，求出A、B间的距离吗？迁移应用解：要测量A、B间的距离，可用如下方法：过点B作AB的垂线BF，在BF上取两点C、D，使CD=BC，再作出BF的垂线DE，使A、C、E在一条直线上，∵∠ACB=ECD∠，CB=CD，∠ABC=EDC∠，∴△EDC≌ABC△（ASA）．∴DE=BA．答：测出DE的长就是A、B之间的距离．CDE【例5】如图,1=2,∠∠点P为BN上的一点，∠PCB+∠BAP=180°，求证:PA=PC.BACN))12P【分析】由角平分线的性质易想到过点P向∠ABC的两边作垂线段PE、PF，构造角平分线的基本图形.EF角平分线的性质与判定5考点解析证明：过点P作PE⊥BA,PF⊥BC,垂足分别为E,F.BACN))12PEF∵∠1=2,∠PE⊥BA,PF⊥BC,垂足分别为E,F.∴PE=PF,∠PEA=∠PFC=90°.∵∠PCB+∠BAP=180°,又∠BAP+∠EAP=180°.∴∠EAP=∠PCB.在△APE和△CPF中，∠PEA=∠PFC=90°，∠EAP=∠FCP，PE=PF，∴△APE≌△CPF(AAS)，∴AP=CP.考点解析【点睛】角的平分线的性质是证明线段相等的常用方法.应用时要依托全等三角形发挥作用.作辅助线有两种思路，一种作垂线段构造角平分线性质基本图；另一种是构造轴对称图形.迁移应用6.如图,1=2,∠∠点P为BN上的一点，PA=PC，求证:∠PCB+∠BAP=180°.BACN))12PEF证明：过点P作PE⊥BA,PF⊥BC,垂足分别为E,F.∵∠1=2,∠PE⊥BA,PF⊥BC,垂足分别为E,F.∴PE=PF,∠PEA=∠PFC=90°.PA=PC，PE=PF，在Rt△APE和Rt△CPF中，∴Rt△PAE≌Rt△PCF(HL).∴∠EAP=∠FCP.∵∠BAP+∠EAP=180°，∴∠PCB+∠BAP=180°.谢谢观看！