等腰三角形(第一课时)-【高效课堂】2022-2023学年八年级数学上学期同步精品课件(人教版)

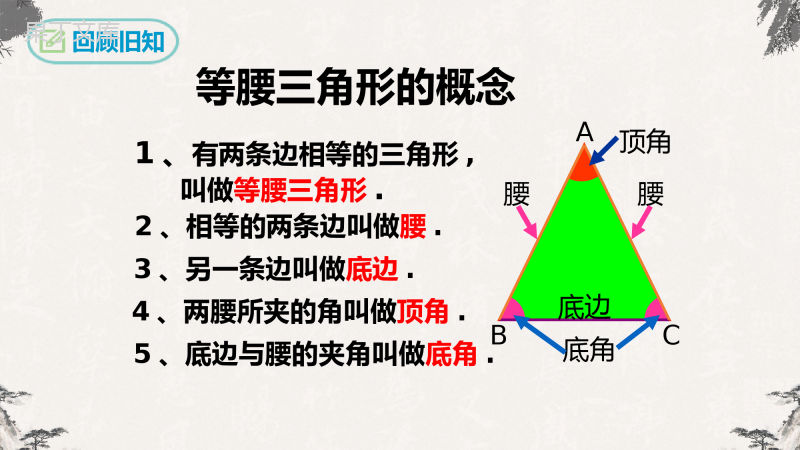
第13.3.1等腰三角形（第一课时）人教版数学八年级上册1、了解等腰三角形的性质，体会等腰三角形“三线合一”的意义.2、探索并掌握等腰三角形的性质，并用以解决实际问题.学习目标ABC1、有两条边相等的三角形,叫做等腰三角形.2、相等的两条边叫做腰.3、另一条边叫做底边.5、底边与腰的夹角叫做底角.4、两腰所夹的角叫做顶角.腰腰底边顶角底角等腰三角形的概念回顾旧知如图所示，把一张长方形的纸按图中虚线对折，并剪去阴影部分，再把它展开，得到的△ABC有什么特点？ABCD合作探究CB把剪出的等腰三角形ABC沿折痕AD对折,找出其中重合的线段和角,填入表中:重合的角重合的线段∠B与∠C∠BAD与∠CAD∠BDA与∠CDA(B)ABD翻折BD与CDAB与ACAD与AD12合作探究重合（相等）的线段重合（相等）的角ACBDAB=ACBD=CD∠B=C∠.∠BAD=∠CAD∠BDA=∠CDA等腰三角形除了两腰相等以外,你还有何发现?小组讨论想想看锐眼发现AD是BC边上的中线AD是∠BAC的角平分线∵∠BDA+∠CDA=1800∴∠BDA=∠CDA=900∴AD是BC边上的高线两底角相等AD=AD合作探究发现2.折痕AD是等腰△ABC的顶角∠BAC的平分线，也是底边BC上的中线还是底边BC上的高。ABCD猜想1.等腰三角形的两个底角相等。2.等腰三角形的顶角平分线,底边上的中线，底边上的高互相重合。如何论证你们的猜想呢？证明一个命题有哪些步骤呢？1.等腰△ABC的两个底角∠B＝∠C。合作探究已知：在△ABC中，AB=AC求证：∠B=C分析：1.如何证明两个角相等？2.如何构造两个全等的三角形？1.等腰三角形的两个底角相等。猜想ABCD论证猜想ADBADCAD证明：作顶角的角平分线即()()ABDACDABACBADCADADADABDACDSASBC在和中全等三角形对应角相等ΔΔΔΔ解法一：已知如图ΔABC中，AB=AC，求证：∠B=∠CABCD论证猜想ADBADCAD证明：作顶角的角平分线即()()ABDACDABACBADCADADADABDACDSASBC在和中全等三角形对应角相等ADBCDBDACDA0证明：作垂直于即==90tttt()()BADCADABACADADBADCADHLBC在R和R中RR全等三角形对应角相等ΔΔΔΔABCD解法二：已知如图ΔABC中，AB=AC，求证：∠B=∠C论证猜想ADBCDBDACDA0证明：作垂直于即==90tttt()()BADCADABACADADBADCADHLBC在R和R中RR全等三角形对应角相等BCDADBDCD证明：取的中点，连接即()()BADCADABACBDCDADADBBADCADCSSS在和中=全等三角形对应角相等ΔΔΔΔABCD解法三：已知如图ΔABC中，AB=AC，求证：∠B=∠C论证猜想BCDADBDCD证明：取的中点，连接即()()BADCADABACBDCDADADBBADCADCSSS在和中=全等三角形对应角相等D如图，作△ABC的中线ADD┌如图，作△ABC的高ADD如图，作顶角的平分线AD.ABCABCABC等腰三角形常见辅助线归纳总结性质1：等腰三角形的两个底角相等。(等边对等角)符号语言：在△ABC中∵AC=AB（已知）∴∠B=C∠（等边对等角）ABC归纳结论练习1.等腰三角形一个底角为70°,求它的顶角是_____.40°变式1.等腰三角形一个角为70°,它的另外两个角为__________________.变式2.等腰三角形一个角为110°,它的另外两个角为_________.35°，35°70°,40°或55°,55°小试牛刀ABDC猜想2.等腰三角形的顶角平分线，底边上的中线，底边上的高互相重合。从猜想1的论证中，你有什么启发呢？论证猜想③作∠A的角平分线AD∴∠BAD=CAD∠在△ABD和△ACD中AB=ACBAD=CAD∠∠AD=ADABDACD(SAS)∴△≌△∴BD=CD,ADB=ADC=90∠∠∴AD是BC边上的中线，也是底边BC上的高①作BC上的中线AD∴BD=CD在△ABD和△ACD中AB=ACAD=ADBD=CD∴△ABDACD(SSS)≌△∴∠BAD=CAD,∠∠ADB=ADC=90°∠∴AD是∠BAC的平分线，也是BC边上的高②作ADBC⊥，垂足为D∴∠ABD=ADC=90°∠在△ABD和△ACD中AB=ACBD=CD∴△ABDACD(HL)≌△∴BD=CD,∠BAD=CAD∠∴AD是BC边上的中线，也是∠BAC的平分线证明：等腰三角形的顶角平分线,底边上的中线，底边上的高互相重合。ABDC论证猜想性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。（可简记为“三线合一”）BADCADBADCADADBCADBCBDCDBDCD符号语言:（1）∵在△ABC中，AB=AC，∠BAD=∠CAD∴⊥，=；（2）∵在△ABC中，AB=AC，BD=CD∴⊥，∴∠=∠；（3）∵在△ABC中，AB=AC，AD⊥BC,∴∠=∠，=。归纳结论归纳：知一推二1.判断：等腰三角形的角平分线、中线和高线互相重合（）2.如图,AB=AC,AD⊥BC交BC于点D,BD=5cm,那么BC的长度为。×10cm小试牛刀例1.如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数。1、图中有哪几个等腰三角形？ABCD△ABC△ABD△BDC2、有哪些相等的角？∠ABC=∠ACB=∠BDC∠A=∠ABD典例精析例1.如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数。xx2x2x2x解：∵AB=AC，BD=BC=AD，∴∠ABC=∠C=∠BDC，∠A=∠ABD(等边对等角)设∠A=x,则∠BDC=∠A+∠ABD=2x,从而∠ABC=∠C=∠BDC=2x,在∆ABC中，有∠A+∠ABC+∠C=x+2x+2x=180°，解得x=36°，在△ABC中，∠A=36°，ABC=∠C=72°典例精析1.如图，在△ABC中，AB=AC,BD=CD,AD的延长线交BC于点E.求证：AE⊥BC。证明：在△BAD与△CAD中AB=ACAD=ADBD=CD∴△BAD≌△CAD(sss)∴∠BAE=∠CAECDABE∵AB=AC∴AE⊥BC拓展训练轴对称图形两个底角相等，简称“等边对等角”顶角平分线、底边上的中线、和底边上的高互相重合，简称“三线合一”学习的数学思想及方法:分类讨论和一题多解。解决等腰三角形问题时常用的辅助线课堂小结课后作业1.如图，在△ABC中，已知AB=AC，D为BC的中点，∠BAD=35°，则∠C的度数为（）A.35°B.45°C.55°D.60°解：∵AB=AC，D为BC的中点，∴∠B=∠C，AD⊥BC.∵∠B=90°-C课后作业解：∵AB=AC=CD，∴∠B=∠C，∠1=∠2．∵BD=AD，∴∠B=∠3．∵∠1=∠B＋∠3，∠B＋∠3＋∠2＋∠C=180°，∴∠B=36°，∠C=36°，∠BAC=108°．2.如图，在△ABC中，点D在BC上，且有AB=AC=CD，BD=AD，求△ABC中各内角的度数．132ABCD谢谢聆听