第十三章-轴对称复习-第2课时(专题讲解)-八年级数学上册同步教材配套精品教学课件(人教版)

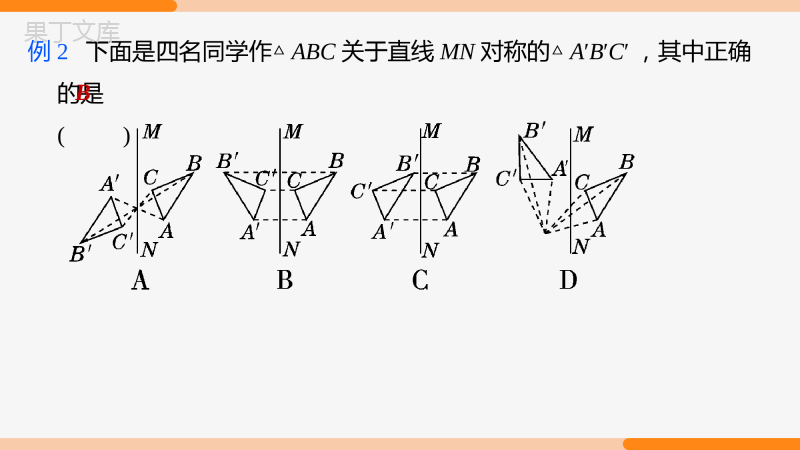
第十三章轴对称专题讲解第十三章轴对称复习全等三角形复习第2课时【学习目标】【学习目标】轴对称复习(第2课时)专题讲解专题一轴对称及轴对称图形专题二线段垂直平分线的性质和判定专题三等腰三角形的性质和判定专题四将军饮马和造桥选址问题专题一轴对称及轴对称图形专题三等腰三角形的性质和判定专题四将军饮马和造桥选址问题专题一轴对称及轴对称图形例1下列“禁止行人通行、注意危险、禁止非机动车通行、限速60km/h”四个交通标志图中，为轴对称图形的是（）ABCDB例2下面是四名同学作△ABC关于直线MN对称的△A′B′C′，其中正确的是()B例3.已知点M(2a－b，5＋a)，N(2b－1，－a＋b)．(1)若点M，N关于x轴对称，试求a，b的值；(2)若点M，N关于y轴对称，试求(b＋2a)99的值．解：(1)由题意得2a－b＝2b－1，5＋a－a＋b＝0，解得a＝－8，b＝－5.即a，b的值分别为－8，－5.解：(2)由题意得2a－b＋2b－1＝0，5＋a＝－a＋b，解得a＝－1，b＝3.∴(b＋2a)99＝(3－2)99＝1.解：(1)由题意得2a－b＝2b－1，5＋a－a＋b＝0，解得a＝－8，b＝－5.即a，b的值分别为－8，－5.解：(2)由题意得2a－b＋2b－1＝0，5＋a＝－a＋b，解得a＝－1，b＝3.∴(b＋2a)99＝(3－2)99＝1.专题二线段垂直平分线的性质和判定例1在△ABC中，AD是高，在线段DC上取一点E，使BD=DE，已知AB+BD=DC.求证：点E在线段AC的垂直平分线上．证明：∵AD是高，∴AD⊥BC.又∵BD=DE，∴AD所在的直线是线段BE的垂直平分线，∴AB=AE，∴AB+BD=AE+DE.又∵AB+BD=DC，∴DC=AE+DE，∴DE+EC=AE+DE,∴EC=AE，∴点E在线段AC的垂直平分线上．例2.如图，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．证明：如图，连接AF.∵AB=AC，∠BAC=120°，∴∠B=∠C=30°.∵AC的垂直平分线是EF，∴CF=AF，∴∠FAC=∠C=30°，∴∠BAF=∠BAC-∠FAC=120°-30°=90°.在Rt△ABF中，∠B=30°，∴BF=2AF，专题三等腰三角形的性质和判定例1等腰三角形的一个内角是另一个内角的2倍，求该等腰三角形的顶角的度数.解：设该等腰三角形中，小角的度数为x,则大角的度数为2x.当x为底角时，x+x+2x=180°，解得x=45°，则2x=90°.当x为顶角时，x+2x+2x=180°，解得x=36°.故该等腰三角形顶角的度数为90°或36°.证明：过点E作EG∥AC交BC于点G，如图，则∠1＝∠F，∠2＝∠3.∵AB＝AC，∴∠B＝∠3(等边对等角)．∴∠B＝∠2.∴BE＝EG(等角对等边)．又∵BE＝CF，∴EG＝CF.例2.如图，在△ABC中，AB＝AC，EF交AB于点E，交AC的延长线于点F，交BC于点D，且BE＝CF.求证：DE＝DF.在△EDG和△FDC中，∠1＝∠F，∠4＝∠5，EG＝FC，∴△EDG≌△FDC(AAS)．∴DE＝DF.12345G例3如图，∠AOP＝∠BOP＝15°，PCOA∥交OB于C，PD⊥OA于D，若PC＝3，求PD的长.解如图，过点P作PE⊥OB于E.∵PCOA∥，∴∠PCE＝∠AOB＝∠BOP＋∠AOP＝30°.又∵PC＝3，∴PE＝1.5.∵∠AOP＝∠BOP，PD⊥OA，∴PD＝PE＝1.5.E专题四将军饮马和造桥选址问题例1按要求完成作图：(1)作△ABC关于y轴对称的△A1B1C1；(2)在x轴上找出点P，使PA+PC最小，并直接写出P点的坐标：xyOABCA1B1C1A'P(-3,0)11例2如图，∠AOB=30°，∠AOB内有一定点P，且OP=10．在OA上有一点Q，OB上有一点R．若△PQR周长最小，则最小周长是（）A．10B．15C．20D．30A课堂练习1.将如图的七巧板的其中几块，拼成一个多边形，为轴对称图形的是()D2.在平面直角坐标系中，若点P(a－3，1)与点Q(2，b＋1)关于x轴对称，则a＋b的值是()A．1B．2C．3D．4C4.如图，已知在△ABC中，AB＝AC，∠C＝30°，AB⊥AD，则下列关系式正确的为()A．BD＝CDB．BD＝2CDC．BD＝3CDD．BD＝4CDB3.在△ABC中,∠A:∠B:∠C=1:2:3,若AB=10,则BC=.55.如图，在△ABC中，AB＝AC，∠A＝36°，BD、CE分别是∠ABC、∠BCD的平分线，则图中的等腰三角形有()A．5个B．4个C．3个D．2个6.一个三角形的一个外角为130°，且它恰好等于一个不相邻的内角的2倍，则这个三角形是（）A．钝角三角形B．直角三角形C．等腰三角形D．等边三角形CA7如图，在△ABC中，AB=AC,BD⊥AC于D.求证：∠BAC=2∠DBC.12E证明：作∠BAC的平分线AE,交BC于点E,如图所示，则∵AB=AC,∴AE⊥BC.∴∠2+∠ACB=90°.∵BD⊥AC,∴∠DBC+∠ACB=90°.∴∠2=∠DBC.∴∠BAC=2∠DBC.ABCD∠1=2=∠∠BAC.7.如图,在△ABC中,AD是角平分线,AC=AB+BD.求证：∠B=2∠C.DCBA证明：在AC上截取AE=AB，连接DE.E∵AD是角平分线，∴∠EAD=∠BAD.又∵AD=AD，∴△EAD≌△BAD，∴DE=DB，∠AED=∠B.∵AC=AB+BD=AE+DE=AE+EC，∴CE=ED.∴∠AED=∠C+∠CDE=2∠C，即∠B=2∠C.想一想：还有别的证明方法吗？提示：延长AB至F，使BF=BD，连接DF.8.如图，已知△ABC是等边三角形，D，E分别为BC、AC上的点，且CD=AE，AD、BE相交于点P，BQ⊥AD于点Q.求证：BP=2PQ.拓展提升∴△ADC≌△BEA.证明：∵△ABC为等边三角形，∴AC=BC=AB，∠C=∠BAC=60°.∵CD=AE，∴∠CAD=∠ABE.∵∠BAP+∠CAD=60°，∴∠ABE+∠BAP=60°.∴∠BPQ=60°.又∵BQ⊥AD，∴BP=2PQ.∴∠PBQ=30°，∴∠BQP=90°，