《综合法和分析法》人教版高中数学选修2-2PPT课件（第2.2.1课时）.pptx

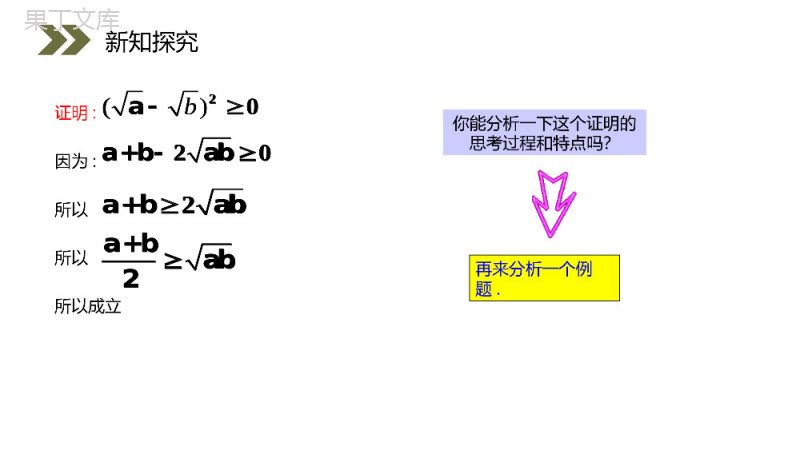
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-22.2.1综合法和分析法第2章推理与证明人教版高中数学选修2-2在以前的学习中，大家已经能应用综合法、分析法证明数学命题，但是对这些证明方法的内涵和特点，大家又了解多少呢？本节课我们对综合法和分析法这些证明方法进行较系统的学习.课前导入不等式：(a>0,b>0)的证明.a+bab2运用以前学过的数学知识，大家自己证明试试看！动动脑新知探究a+bab2你能分析一下这个证明的思考过程和特点吗？证明:因为:所以所以所以成立()b20a20a+bab2a+baba+bab2再来分析一个例题.新知探究()b20a20a+bab2a+baba+bab2已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc提示首先，分析待证不等式的特点：不等式的右端是3个数a,b,c乘积的4倍，左端为两项之和，其中每一项都是一个数与另两个数的平方和之积.据此，只要把两个数的平方和转化为这两个数的积的形式，就能使不等式左、右两端具有相同的形式.新知探究其次，寻找转化的依据及证明中要用的其他知识：应用不等式x2+y2≥2xy就能实现转化，不等式的基本性质是证明的依据.最后，给出具体证明：由b2+c2≥2ab及条件a>0，得a(b2+c2)≥2abc；类似地，得b(c2+a2)≥2abc.从而有a(b2+c2)+b(c2+a2)≥4abc.新知探究证明:∵b2+c2≥2bc,a>0∴a(b2+c2)≥2abc.又∵c2+b2≥2bc,b>0∴b(c2+a2)≥2abc.∴a(b2+c2)+b(c2+a2)≥4abc.新知探究探究思考…这些证明过程有什么相似点？这些证明过程都是从已知条件和某些数学定义、公理、定理等出发，通过推理推导出所要的结论.新知探究一般地，利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法.其特点是“由因导果”.新知探究知识要点则综合法可用框图表示如下：用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.1PQ12QQ23QQ…nQQ你能用框图表示综合法吗？新知探究1PQ12QQ23QQnQQ在△ABC中，三个内角A、B、C对应的边分别为a、b、c，且A、B、C成等差数列，a、b、c成等比数列，求证△ABC为等边三角形．分析•将A，B，C成等差数列，转化为符号语言就是2B=A+C；新知探究此时，如果能把角和边统一起来，那么就可以进一步寻找角和边之间的关系，进而判断三角形的形状，余弦定理正好满足要求.于是，可以用余弦定理为工具进行证明.•a，b，c成等比数列转化为符号语言就是2b=ac.•A，B，C为△ABC的内角，这是一个隐含条件，即A+B+C=180°；新知探究2b=ac.证明：由A，B，C成等差数列，有2B=A+C.①因为A，B，C为△ＡＢC的内角,所以Ａ+Ｂ+Ｃ=180°.②πB=.3③由a，b，c成等比数列，有2b=ac.④由①②，得①②，得由①②，得新知探究由余弦定理及③，可得22222b=a+c-2accosB=a+c-ac.再由④，得22a+c-ac=ac,即2a-c=0.（）因此a=c.从而A=C.⑤πB=.32b=ac.22222b=a+c-2accosB=a+c-ac.22a+c-ac=ac,2a-c=0.（）由②③,得πA=B=C=.3所以△ＡＢC为等边三角形.注意解决数学问题时，往往要先做语言的转换，如把文字语言转换成符号语言，或把符号语言转换成图形语言等.还要通过细致的分析，把其中的隐含条件明确表示出来.⑤新知探究πA=B=C=.3不等式：(a>0,b>0)的证明.a+bab2动动脑大家想一想，除了综合法，还有别的证明方法吗？新知探究a+bab2证明:要证只需证:只需证:只需证:因为:成立所以成立a+bab22a+bab20a+bab()b20a()b20aa+bab2类比综合法，你能分析一下这个证明的思考过程和特点吗？新知探究a+bab22a+bab20a+bab()b20a()b20aa+bab2要证明结论成立，逐步寻求推证过程中，使每一步结论成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止.这类证法的特点是:这就是另一种证明方法——分析法.新知探究一般地，从要证明的结论出发，逐步寻求推证过程中，使每一步结论成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件（已知条件、定理、定义、公理等）为止，这种证明的方法叫做分析法．新知探究知识要点类似综合法，我们也可以后框图来表示分析法：1QP23PP12PP得到一个明显成立的结论…分析法的适用范围：当已知条件与结论之间的联系不够明显、直接，证明中需要用哪些知识不太明确具体时，往往采用从结论出发，结合已知条件，逐步反推，寻求使当前命题成立的充分条件的方法.注意新知探究1QP23PP12PP分析3+7<25.求证从待证不等式不易发现证明的出发点，因此我们直接从待证不等式出发，分析其成立的充分条件.新知探究3+7<25.求证证明：3+7<25，只需证223+7<25.（）（）展开得10+221<20，只需证21<5，因为和都是正数，所以要证3+725新知探究3+7<25，223+7<25.（）（）10+221<20，21<5，3+725只需证21<25.因为21<25成立，所以成立.3+7<25，反思在本例中，如果我们从“21<25”出发，逐步倒推回去，就可以用综合法证出结论.但由于我们很难想到从“21<25”入手，所以用综合法比较困难.新知探究3+7<25，请对综合法与分析法进行比较，说出它们各自的特点.回顾以往的数学学习，说说你对这两种证明方法的新认识.综合法就是利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立.分析法最大的特点就是执果索因.新知探究注意事实上，在解决问题时，我们把综合法和分析法结合起来使用：根据条件的结构特点去转化结论，得到中间结论；根据结论的结构特点去转化条件，得到中间结论.若由可以推出成立，就可以证明结论成立.Q＇P＇P＇Q＇Q＇P＇P＇Q＇22222πα,βkπ+(kZ),2sinθ+cosθ=2sinα1sinθgcosθ=sinβ21-tanα1-tanβ=.1+tanα2(1+tanβ)≠例，已知且（）（）求证新知探究22222πα,βkπ+(kZ),2sinθ+cosθ=2sinα1sinθgcosθ=sinβ21-tanα1-tanβ=.1+tanα2(1+tanβ)≠例，已知且（）（）分析比较已知条件和结论，发现结论中没有出现角，因此第一步工作可以从已知条件中消去.观察已知条件的结构特点，发现其中蕴含数量关系，于是，由(1)×(1)-2(2)得.把它与结论相比较，发现角相同，但函数名不同.θθ2sinθ+cosθ-2sinθcosθ=1（）224sinα-2sinβ=1新知探究于是尝试转化结论：统一函数名称，即把正切函数化为正（余）弦函数.把结论转化为再与比较，发现只要把的角的余弦转化为正弦，就能达到目的.22221cosα-sinα=(cosβ-sinβ)2224sinα-2sinβ=122221cosα-sinα=(cosβ-sinβ)2θθ2sinθ+cosθ-2sinθcosθ=1（）224sinα-2sinβ=122221cosα-sinα=(cosβ-sinβ)2224sinα-2sinβ=122221cosα-sinα=(cosβ-sinβ)2证明：,22222222222222222sinθ+cosθ-2sinθcosθ=14sinα-2sinβ=1.1-tanα1-tanβ=1+tanα2(1+tanβ)sinβsinα1-1-cosβcosα=sinαsinβ1+2(1+)cosαcosβ（），，因为所以将(1)(2)代入，可得另一方面要证即证新知探究,22222222222222222sinθ+cosθ-2sinθcosθ=14sinα-2sinβ=1.1-tanα1-tanβ=1+tanα2(1+tanβ)sinβsinα1-1-cosβcosα=sinαsinβ1+2(1+)cosαcosβ（），，因为所以将(1)(2)代入，可得另一方面要证即证222222221cosα-sinα=(cosβ-sinβ)211-2sinα=(1-2sinβ)24sinα-2sinβ=1.，，即证即证即证由于上式与③相同，于是问题得证.新知探究222222221cosα-sinα=(cosβ-sinβ)211-2sinα=(1-2sinβ)24sinα-2sinβ=1.，，即证即证即证如图，在直四棱柱ABCD-1234ABCD为等腰梯形，AB//CD,AB=4,BC=CD=2,中，底面ABCD11111AA=2EEFADAAAB.1EE//FCC，、、分别是棱、、的中点（）证明：直线平面；ABCDEF1E1A1C1D1B课堂练习的平行线，这就需要借助辅助线，1EE要证//平面1FCC，只需在平面1FCC内找到1EE111111ABFADCF.CF.取的中点，连接，为得到的平行线解：分析（1）FABCDE1E1A1C1D1B1F1234ABCD11111AA=2EEFADAAAB.1EE//FCC，、、分别是棱、、的中点（）证明：直线平面；1E1A1C1D1B1EE1FCC1FCC1EE111111ABFADCF.CF.取的中点，连接，为得到的平行线1E1A1C1D1B1F11111111111111111111111111ABCD-ABCDABFADCF.AB=4CD=2AB//CDCDAFAFCDCF//ADEEADAAEE//AD//CFEEFCCCFFCCEE//FCC.在直四棱柱中，取的中点，连接，得到直线因为，且，所以平行且等于，为平行四边形，所以，又因为、分别是棱、的中点，所以，又因为平面，⊂平面，所以直线平面课堂练习11111111111111111111111111ABCD-ABCDABFADCF.AB=4CD=2AB//CDCDAFAFCDCF//ADEEADAAEE//AD//CFEEFCCCFFCCEE//FCC.在直四棱柱中，取的中点，连接，得到直线因为，且，所以平行且等于，为平行四边形，所以，又因为、分别是棱、的中点，所以，又因为平面，⊂平面，所以直线平面2.如图,SA⊥平面ABC,ABBC,⊥过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F,求证AFSC.⊥FESCBA提示此题采用分析法.课堂练习证明:要证AFSC⊥只需证:SC⊥平面AEF只需证:AESC⊥只需证:AE⊥平面SBC只需证:AEBC⊥只需证:BC⊥平面SAB只需证:BCSA⊥只需证:SA⊥平面ABC因为:SA⊥平面ABC成立所以.AFSC⊥成立FESCBA课堂练习1.综合法的概念：一般地，利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法.课堂小结2.分析法的概念:一般地，从要证明的结论出发，逐步寻求推证过程中，使每一步结论成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件（已知条件、定理、定义、公理等）为止，这种证明的方法叫做分析法．3.分析法的适用范围：当已知条件与结论之间的联系不够明显、直接，证明中需要用哪些知识不太明确具体时，往往采用从结论出发，结合已知条件，逐步反推，寻求使当前命题成立的充分条件的方法.4.在证明数学问题时，通常把综合法和分析法结合起来使用.感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-2感谢你的聆听第2章推理与证明人教版高中数学选修2-2