画轴对称图形(第二课时)-【高效课堂】2022-2023学年八年级数学上学期同步精品课件(人教版)

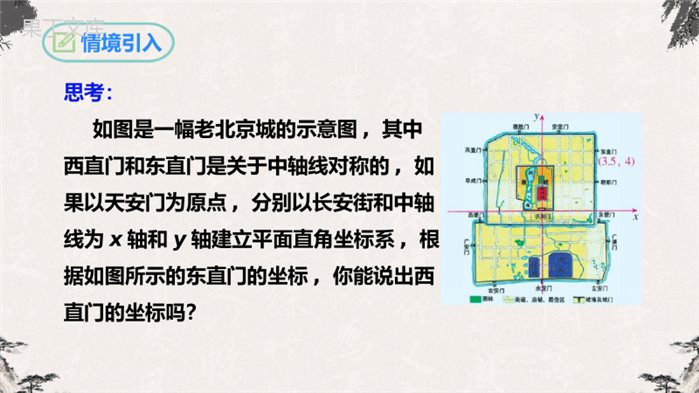
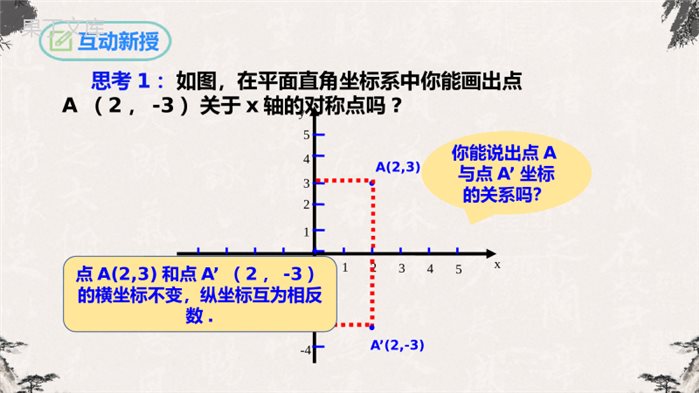
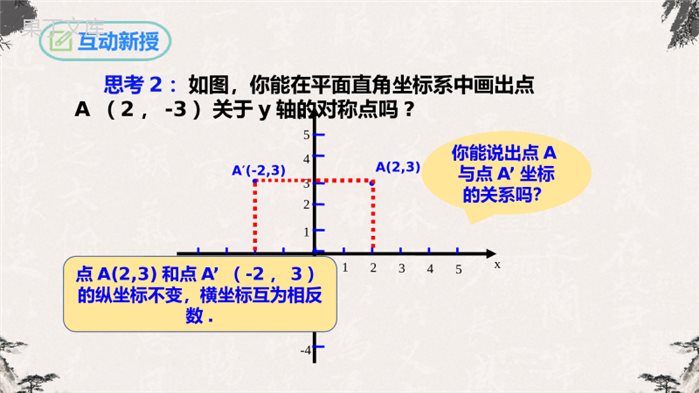
第13.2画轴对称图形（第二课时）人教版数学八年级上册1、理解在平面直角坐标系中,已知点关于x轴、y轴对称的点的坐标的变化规律.2、掌握在平面直角坐标系中作出一个图形的轴对称图形的方法.学习目标情境引入思考：如图是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的,如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系,根据如图所示的东直门的坐标,你能说出西直门的坐标吗？互动新授·31425-2-4-1-3012345-4-3-2-1A(2,3)xy思考1：如图，在平面直角坐标系中你能画出点A（2，-3）关于x轴的对称点吗?·A’(2,-3)你能说出点A与点A’坐标的关系吗？点A(2,3)和点A’（2，-3）的横坐标不变，纵坐标互为相反数.思考2：如图，你能在平面直角坐标系中画出点A（2，-3）关于y轴的对称点吗?互动新授·31425-2-4-1-3012345-4-3-2-1A(2,3)xy·A′(-2,3)你能说出点A与点A’坐标的关系吗？点A(2,3)和点A’（-2，3）的纵坐标不变，横坐标互为相反数.互动新授在平面直角坐标系中,画出下列已知点及其关于坐标轴的对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律,再和同学讨论一下.已知点A（2,-3）B（-1,2）C（-6,-5）D（,1）E（4,0）关于x轴的对称点关于y轴的对称点2121已知点A（2,-3）B（-1,2）C（-6,-5）D（,1）E（4,0）关于x轴的对称点A′（2,3）B′（-1,-2）C′（-6,5）D′（,-1）E′（4,0）2121互动新授2121已知点A（2,-3）B（-1,2）C（-6,-5）D（,1）E（4,0）关于y轴的对称点A′′（-2,-3）B′′（1,2）C′′（6,-5）D′′（,1）E′′（-4,0）2121-互动新授2121-根据表格所填的坐标,你发现了什么规律？已知点A（2,-3）B（-1,2）C（-6,-5）D（,1）E（4,0）关于x轴的对称点A′（2,3）B′（-1,-2）C′（-6,5）D′（,-1）E′（4,0）2121关于y轴的对称点A′′（-2,-3）B′′（1,2）C′′（6,-5）D′′（,1）E′′（-4,0）21-互动新授212121-总结归纳关于坐标轴对称的点的坐标规律：1.点（x,y）关于x轴对称的点的坐标是（x,-y）,特点是横坐标相同,纵坐标互为相反数.2.点（x,y）关于y轴对称的点的坐标是（-x,y）,特点是纵坐标相同,横坐标互为相反数.典例精析例2.如图，四边形ABCD的四个顶点的坐标分别为A（-5,1）,B（-2,1）,C（-2,5）,D（-5,4）,分别画出与四边形ABCD关于x轴和y轴对称的图形.典例精析已知点A（-5,1）B（-2,1）C（-2,5）D（-5,4）关于x轴的对称点A′（-5,-1）B′（-2,-1）C′（-2,-5）D′（-5,-4）典例精析已知点A（-5,1）B（-2,1）C（-2,5）D（-5,4）关于y轴的对称点A′′（5,1）B′′（2,1）C′′（2,5）D′′（5,4）小试牛刀1.点P(,6)与点Q关于x轴对称，则点Q的坐标为_______.(5,6)2.点M(a,5)与点N(2,b)关于x轴对称，则a=___,b=___.253.点P(5,6)与点Q关于y轴对称，则点Q的坐标_______.4.点M(a,5)与点N(2,b)关于y轴对称，则a=____,b=_____.（5，6）251.分别写出下列各点关于x轴和y轴对称的点的坐标：（-2，6），（1，-2），（-1，3），（-4，-2），（1，0）解：点（-2，6）关于x轴对称的点的坐标为（-2，-6），关于y轴对称的点的坐标为（2，6）.点（1，-2）关于x轴对称的点的坐标为（1，2），关于y轴对称的点的坐标为（-1，-2）.点（-1，3）关于x轴对称的点的坐标为（-1，-3），关于y轴对称的点的坐标为（1，3）.点（-4，-2）关于x轴对称的点的坐标为（-4，2），关于y轴对称的点的坐标为（4，-2）.点（1，0）关于x轴对称的点的坐标为（1，0），关于y轴对称的点的坐标为（-1，0）.课堂检测课堂检测2.如图，△ABC的顶点都在正方形网格格点上，点A的坐标为（1,4）.将△ABC沿y轴翻折到第一象限，则点C的对应点C'的坐标是（）A.(3,1)B.(3,1)C.(1，3）D.(3，1）xyOCBAA在平面直角坐标系中,△ABC的顶点坐标分别为A（-4,1）,B（-2,1）,C（-2,3）.（1）作△ABC关于y轴对称的△A1B1C1；（2）将△ABC向下平移4个单位长度；做出平移后的△A2B2C2；（3）求四边形AA2B2C的面积.拓展训练（1）△ABC的顶点坐标分别为A（-4,1）,B（-2,1）,C（-2,3）,关于y轴对称的点分别为A1（4,1）,B1（2,1）,C1（2,3）.拓展训练（2）△ABC的顶点坐标分别为A（-4,1）,B（-2,1）,C（-2,3）,向下平移4个单位长度的点分别为A1（-4,-3）,B1（-2,-3）,C1（-2,-1）.拓展训练（3）四边形AA2B2C为梯形,其中上底AA2=4,下底B2C=6,高A2B2=2,所以四边形AA2B2C的面积为10.拓展训练课堂小结1．在平面直角坐标系中，已知点关于x轴或y轴的对称点的坐标有什么变化规律？2．画一个图形关于x轴或y轴对称的图形的方法和步骤．点（x，y）关于x轴对称的点的坐标为（x，-y）；点（x，y）关于y轴对称的点的坐标为（-x，y）．（1）求特殊点的坐标；（2）描点；（3）连线．1.如图，△ABC在平面直角坐标系中第二象限内，顶点A的坐标是（-2，3），先把△ABC向右平移4个单位得到△A1B1C1，再作△A1B1C1关于x轴对称图形△A2B2C2，则顶点A2的坐标是（）A．（-3，2）B．（2，-3）C．（1，-2）D．（3，-1）B2.线段MN在直角坐标系中的位置如图所示，若线段M′N′与MN关于y轴对称，则点M的对应点M′的坐标为（）A．（4，2）B．（-4，2）C．（-4，-2）D．（4，-2）D课后作业3.已知点A(m-1,3)与点B(2,n+1)关于x轴对称，则m=_____,n=______.3-44.若点P关于x轴对称点为P1(2a+b,-a+1),关于y轴对称点P2(4-b,b+2),则点P的坐标为_____________.(-9,-3)5.将点A（3，2）沿x轴向左平移4个单位长度得到点A′，点A′关于y轴对称的点的坐标是__________.(1,2)课后作业谢谢聆听