《二项式定理》人教版高中数学选修2-3PPT课件（第1.3.1课时）.pptx

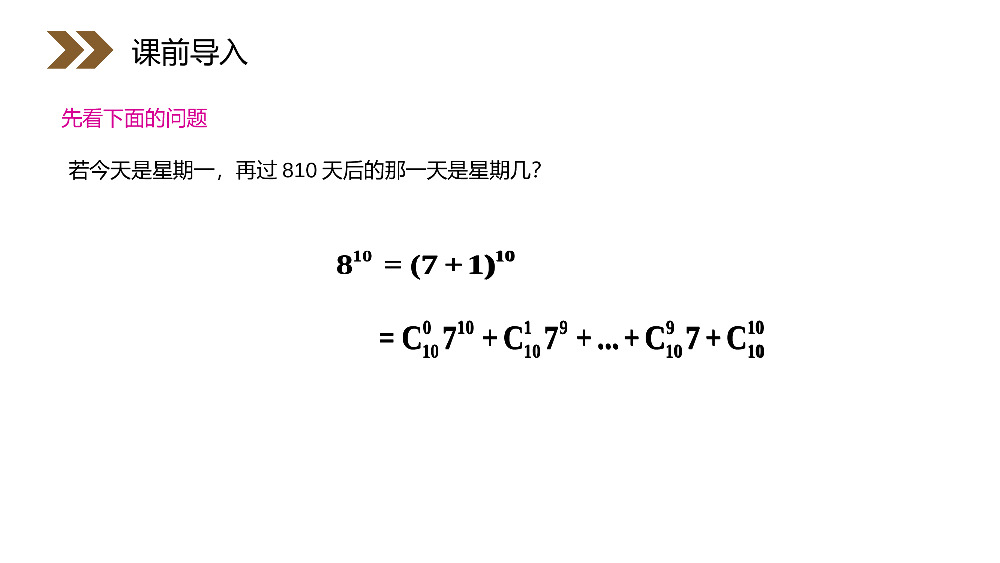
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-31.3.1二项式定理第1章计数原理人教版高中数学选修2-3先看下面的问题若今天是星期一，再过810天后的那一天是星期几？10108=(7+1)0101991010101010=C7+C7+...+C7+C课前导入10108=(7+1)0101991010101010=C7+C7+...+C7+C在初中，我们已经学过了(a+b)2=a2+2ab+b2(a+b)3＝(a+b)2(a+b)＝a3+3a2b+3ab2+b3观察对于(a+b)4，(a+b)5如何展开?课前导入(a+b)100又怎么办？(a+b)n(nN∈+)呢？我们知道，事物之间或多或少存在着规律.这节课，我们就来研究(a+b)n的二项展开式的规律性.规律：(a+b)1=a+b(a+b)2=(a+b)(a+b)=a•a+a•b+b•a+b•b=a2+2ab+b2(a+b)3=(a+b)2(a+b)=(a2+2ab+b2)(a+b)=a3+3a2b+3ab2+b3(a+b)4=(a+b)3(a+b)=(a3+3a2b+3ab2+b3)(a+b)=a4+4a3b+6a2b2+4ab3+b4新知探究如何从组合知识得到(a+b)4展开式中各项的系数?(a+b)4=(a+b)(a+b)(a+b)(a+b)(1)若每个括号都不取b，只有一种取法得到a4；(2)若只有一个括号取b，共有种取法得到a3b；(3)若只有两个括号取b，共有种取法得到a2b2；(4)若只有三个括号取b，共有种取法得到ab3；(5)若每个括号都取b，共有种取法得b4.新知探究1二项式定理n0n1n-11nn(a+b)=Ca+Cab+...+kn-kknnnnCab+...+Cb(nN).新知探究知识要点n0n1n-11nn(a+b)=Ca+Cab+...+kn-kknnnnCab+...+Cb(nN).如何证明上述猜想呢？证明：由于(a+b)n是（a+b）相乘，每个（a+b）在相乘时有两种选择，选a或b，而且每个（a+b）中的a或b都选定后，才能得到展开式的一项.因此，由分步乘法计数原理可知，在合并同类项之前，(a+b)n的展开式共有2n项，其中每一项都是an-kbk（k=0，1，…，n）的形式.新知探究对于某个k（），对应的项an-kbk是由n-k个（a+b）中选a，k个（a+b）中选b得到的.由于b选定后，a的选法也随之确定.因此，an-kbk出现的次数相当于从n个(a+b)中取k个b的组合数.这样，(a+b)n的展开式中，an-kbk共有个，将它们合并同类项，就可以得到二项展开式：k0,1,2,...,nknCknCn0n1n-1kn-kknnnnnn(a+b)=Ca+Cab+...+Cab+...+Cb.k0,1,2,...,nknCknCn0n1n-1kn-kknnnnnn(a+b)=Ca+Cab+...+Cab+...+Cb.对二项式定理的理解（1）它有n+1项;（2）各项的次数都等于二项式的次数n;（3）字母a按降幂排列，次数由n递减到0;字母b按升幂排列，次数由0递增到n.新知探究2二项式系数我们看到的二项展开式共有n+1项，其中各项的系数()叫做二项式系数（binomialcoefficient）.k0,1,2,...,nknC新知探究知识要点3通项式中的叫做二项展开式的通项，用Tk+1表示，即通项为展开式的第k+1项：kn-kknCabkn-kkk+1nT=Cabk0,1,2,...,nknCkn-kknCabkn-kkk+1nT=Cab对通项的理解（1）它是(a+b)n的展开式的第k+1项，这里k=0，1，2，…，n;（2）字母a，b是一种“符号”，实际上它们可以是数、式及其它什么的，只要具备二项式的形式就可以用定理写出展开式;（3）展开式是对(a+b)n这个标准形式而言的，还可以对等式进行变形.新知探究例题1用二项式定理展开下列各式：64)x1x(2(2))x1(x(1)思考（1）如何求展开式中的第三项？（2）如何求展开式中第三项的系数？方法（1）用定理展开，再找指定项；（2）用通项公式.新知探究64)x1x(2(2))x1(x(1)解:313444411+Cx()+C()xx422411=x+4x+6+4()+()xx404131222444111(1)(x+)=Cx+Cx()+Cx()xxx新知探究（2）先将原式化简，再展开，得666312x-11(2x-)=()=(2x-1)xxx6152433425666666631=(2x)-C(2x)+C(2x)-C(2x)+C(2x)-C(2x)+Cx6543231=(64x-632x+1516x-208x+154x-62x+1)x322360121=64x-192x+240x-160+-+.xxx313444411+Cx()+C()xx422411=x+4x+6+4()+()xx404131222444111(1)(x+)=Cx+Cx()+Cx()xxx666312x-11(2x-)=()=(2x-1)xxx6152433425666666631=(2x)-C(2x)+C(2x)-C(2x)+C(2x)-C(2x)+Cx6543231=(64x-632x+1516x-208x+154x-62x+1)x322360121=64x-192x+240x-160+-+.xxx例题21.的展开式中，第五项是……（）A.B.C.D.2.的展开式中，不含a的项是第（）A.7项B.8项C.9项D.6项62)xaax(x1532a6xx20x15153)a1a(新知探究答案：(1)B(2)A62)xaax(x1532a6xx20x15153)a1a(例题3求近似值（精确到0.001）（1）(0.997)3（2）(1.002)6分析：（1）(0.997)3=(1-0.003)3（2）(1.002)6=(1+0.002)6类似这样的近似计算转化为二项式定理求展开式，按精确度展开到一定项.新知探究例题44.求二项式的展开式中的有理项.73)213(分析：方法一用通项公式（适用于任意次幂）方法二用定理展开（次数较小时使用）答案：4105新知探究73)213(41051.在的展开式中，常数项是______.A.14B.－14C.42D.－4273)x1(2x课堂练习解析：,x21)(C)x1()(2xCk2721k7kk7kk73k71kT0,k27211421)(C667则k=6，故展开式中的常数项是,选答案A.令73)x1(2x,x21)(C)x1()(2xCk2721k7kk7kk73k71kT0,k27211421)(C6672.在(x-a)10的展开式中，x7的系数是15，则实数a的值为_______.-1/2.21a15,aC,x1)(aCa)(xCT33107333103731013解析：课堂练习.21a15,aC,x1)(aCa)(xCT331073331037310131.填空（1）(x+2)10(x2-1)的展开式中x10的系数为_____.（2）在(x-1)11的展开式中，x的偶次幂的所有项的系数的和为______.1.179-210课堂练习2.选择（1）(i)12展开式中所有奇数项的和是()A.-1B.1C.0D.i（2）数11100-1的末尾连续的零的个数是()A.0B.3C.5D.7√√13+22课堂练习13+22)r＝C12r3.解答题（1）求(+)12展开式中所有的有理数项.33r422r3解：通项为Tr+1＝C12r()12-r((r＝0,1,2，…，12)，为得有理数项，只需r是6的倍数，即r＝0,6,12，即有理数项为T1＝C120·24＝16，T7＝C126·22·33＝99792，T13＝C1212·36＝729.32332课堂练习33r422r332332（2）二项式的展开式中第三项系数比第二项系数大44，求第4项的系数.分析：由第三项系数比第二项系数大44先求n，再由通项求第四项系数.答案：165n4)x1x(x课堂练习n4)x1x(x(3)某班有男、女学生各n人，现在按照男生至少一人，女生至多n人选法，将选出的学生编成社会实践小组，试证明：这样的小组的选法共有2n(2n-1)种.证：依题意，这些小组中女生人数分别是Cn0，Cn1,Cn2,…,Cnn个.对于上述女生人数的每种情况，男生人数可以有Cn0，Cn1,Cn2,…,Cnn个。课堂练习根据乘法原理和加法原理可得Cn0Cn1+Cn0Cn2+…+Cn0Cnn+Cn1Cn1+…+Cn1Cn2+Cn2Cn1+Cn2Cn2+…+Cn2Cnn+…CnnCn1+CnnCn2+…+CnnCnn＝Cn0(Cn1+Cn2+…+Cnn)+Cn1(Cn1+Cn2+…+Cnn)+Cn2(Cn1+Cn2+…+Cnn)+…+Cnn(Cn1+Cn2+…+Cnn)＝(Cn1+Cn2+…+Cnn)(Cn0+Cn1+Cn2+…+Cnn)＝(2n-1)2n∴依题意所编成的小组共有2n(2n-1)个.课堂练习1.二项式定理二项式定理(a+b)n=Cn0an+Cn1an-1b+…+Cnran-rbr+…+Cnnbn是通过不完全归纳法，并结合组合的概念得到展开式的规律性，然后用数学归纳法加以证明.课堂小结2.二项式定理的特点(1)项数：共n+1项,是关于a与b的齐次多项式(2)系数(3)指数：a的指数从n逐项递减到0,是降幂排列；b的指数从0逐项递增到n，是升幂排列.感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-3感谢你的聆听第1章计数原理人教版高中数学选修2-3