2022-2023学年人教版数学九年级上册--实际问题与一元二次函数(2)-课件

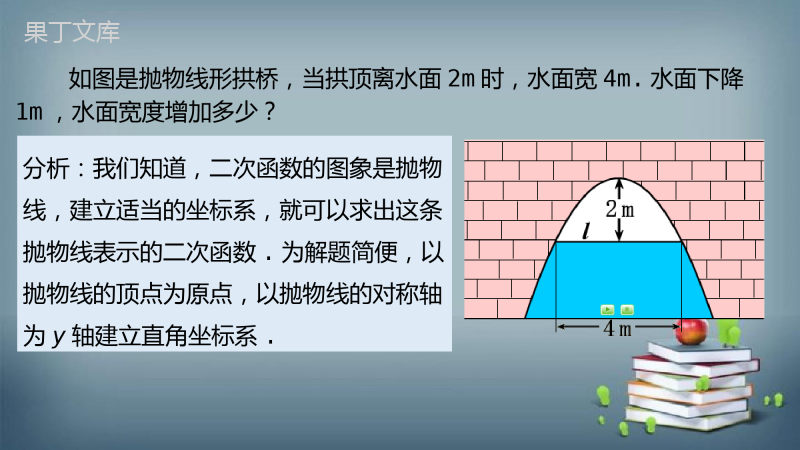
22.3.2实际问题与一元二次函数（2）教学目标知识与智能：1、使学生掌握根据实际问题列出二次函数关系式的方法，并了解如何根据实际问题确定自变量的取值范围。2、会运用二次函数的顶点坐标求出实际问题的最大值（或最小值）。过程与方法：实际问题让学生经历数学建模的基本过程，体会建立数学建模的思想情感、态度、价值观：体会二次函数是一类最优化问题的重要数学模型，感受数学的应用价值，提高学生用数学的意识。教学重难点教学重点：探究利用二次函数的最大值（或最小值）解决实际问题的方法。教学难点：如何将实际问题转化为二次函数的问题，并利用函数的性质进行决策。1.函数y=ax2(a≠0)的图象是一条_______，它的顶点坐标是_______，对称轴是_____，当a____时，开口向上，当a____时，开口向下.2.二次函数解析式的形式有：①一般式：____________，②顶点式：_____________，③交点式：________________.3.(1)如图所示的抛物线，可以根据顶点所在的位置设为_________，也可以根据抛物线与x轴的交点坐标设为______________.(2)由A，B两点的横坐标，可以求得线段AB的长为______.抛物线(0,0)y轴＞0＜0y=ax2+bx+cy=a(x-h)2+ky=a(x-x1)(x-x2)y=ax2+2y=a(x+2)(x-2)4如图是抛物线形拱桥，当拱顶离水面2m时，水面宽4m.水面下降1m，水面宽度增加多少？分析：我们知道，二次函数的图象是抛物线，建立适当的坐标系，就可以求出这条抛物线表示的二次函数.为解题简便，以抛物线的顶点为原点，以抛物线的对称轴为y轴建立直角坐标系.如图是抛物线形拱桥，当拱顶离水面2m时，水面宽4m.水面下降1m，水面宽度增加多少？解：以抛物线的顶点为原点，以抛物线的对称轴为y轴建立直角坐标系.设这条抛物线表示的二次函数为y=ax2.由抛物线经过点(2，-2)，可得-2=a×22，解得，a=-∴这条抛物线表示的二次函数为：y=-x2当水面下降1m时，水面的纵坐标为-3.当y=-3时，x=±.∴当水面下降1m时，水面的宽度为2m.∴水面的宽度增加了(2-4)m.你有其它解法吗？如图是抛物线形拱桥，当拱顶离水面2m时，水面宽4m.水面下降1m，水面宽度增加多少？解：以离拱顶2m时的水面为x轴，以抛物线的对称轴为y轴建立直角坐标系.设这条抛物线表示的二次函数为y=ax2+2.由抛物线经过点(2，0)，可得0=a×22+2，解得，a=-∴这条抛物线表示的二次函数为：y=-x2+2当水面下降1m时，水面的纵坐标为-1.当y=-1时，x=±.∴当水面下降1m时，水面的宽度为2m.∴水面的宽度增加了(2-4)m.在“拱桥类”问题中，一般知道拱高和拱长，这时可根据抛物线的对称性建立以对称轴为y轴的坐标系，然后根据所建立的坐标系，确定抛物线上一些点的坐标.若顶点在原点上，一般设二次函数的解析式为y=ax2；若顶点不在原点上，一般设二次函数的解析式为y=ax2+k.步骤：(1)恰当地建立直角坐标系；(2)将已知条件转化为点的坐标；(3)合理地设出所求函数关系式；(4)代入已知条件或点的坐标求出关系式；(5)利用关系式求解问题.例1.如图，隧道的截面由抛物线和长方形构成,长方形的长是8m，宽是2m，抛物线可以用y=-0.25x2+4表示.(1)一辆高5.2m，宽2m的货运卡车能通过该隧道吗?(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过?解:(1)建立相应的坐标系.当货运卡车在正中央时,即对应的x=±1，y=3.75.∵3.75+2>5.2∴它能通过该隧道(2)当隧道内设双行道时，就意味着货运卡车只能走一边，即对应的x=±2，y=3.∵3+2＜5.2∴它不能通过该隧道.例2.某公司草坪的护栏是由50段形状相同的抛物线组成的，为牢固起见，每段护栏需按间距0.4m加设不锈钢管如图做成的立柱，为了计算所需不锈钢立柱的总长度,设计人员测得如图所示的数据.(1)求该抛物线的解析式;(2)计算所需不锈钢管的总长度.解:(1)以0为原点建立直角坐标.设此抛物线解析式为y=ax(x-2),依题意得，抛物线顶点坐标为(1，0.5)∴0.5=a×1×(1-2)，解得a=-∴该抛物线的解析式为y=-x(x-2)，即y=-x2+x.例2.某公司草坪的护栏是由50段形状相同的抛物线组成的，为牢固起见，每段护栏需按间距0.4m加设不锈钢管如图做成的立柱，为了计算所需不锈钢立柱的总长度,设计人员测得如图所示的数据.(1)求该抛物线的解析式;y=-x2+x(2)计算所需不锈钢管的总长度.解:(2)依题意得:当x=0.4时，y=0.32当x=0.8时，y=0.48当x=1.2时，y=0.48当x=1.6时，y=0.32所需不锈钢管的总长度为50×2×(0.32+0.48)=80m.例3.如图，已知排球场的长度OD为18米，位于球场中线处的球网AB的高度2.24米，一队员站在点0处发球,排球从点0的正上方2米的C点向正前方飞去，排球的飞行路线是抛物线的一部分，当排球运行至离点0的水平距离OE为6米时,到达最高点G，以0为原点建立如图所示的平面直角坐标系.(1)若排球运行的最大高度为2.8米，求排球飞行的高度p(单位:米)与水平距离x(单位:米)之间的函数关系式;解:(1)由题意知顶点G的坐标为(6，2.8)，则设抛物线的解析式为p=a(x-6)2+2.8∵点C坐标为(0，2)，且在抛物线上∴2=a(0-6)2+2.8，解得a=-.例3.如图，已知排球场的长度OD为18米，位于球场中线处的球网AB的高度2.24米，一队员站在点0处发球,排球从点0的正上方2米的C点向正前方飞去，排球的飞行路线是抛物线的一部分，当排球运行至离点0的水平距离OE为6米时,到达最高点G，以0为原点建立如图所示的平面直角坐标系.(2)在(1)的条件下，这次所发的球能够过网吗?如果能够过网，是否会出界?请说明理由;解:(2)当x=9时，p=-×(9-6)2+2.8=2.6>2.24当x=18时，p=-×(18-6)2+2.8=-0.4<0故这次发球可以过网且不出边界(3)若该队员发球要想过网，又使排球不会出界(排球压线属于没出界)，求二次函数中二次项系数的最大值.解:(3)设抛物线的解析式为p=a(x-6)2+h将点C(0，2)代入得36a+h=2，即h=2-36a∴p=a(x-6)2+2-36a根据题意,不出边界时有a(18-6)2+2-36a≤0，解得a≤-要使排球过网，则a(9-6)2+2-36a≥2.24，解得a≤-故二次函数中二次项系数的最大值为-1.足球被从地面上踢起，它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示，其中t(s)表示足球被踢出后经过的时间，则球在____s后落地.2.某广场有一喷水池,水从地面喷出，如图所示，以水平地面为x轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分，则水喷出的最大高度是____米.443.有一个抛物线形桥拱,其最大高度为16米，跨度为40米,现在它的示意图放在平面直角坐标系中(如右图),则此抛物线的解析式为__________________.4.在一次羽毛球比赛中，某次羽毛球的运动路线可以看作是抛物线y=-元2+bx+c的一部分(如图)，其中出球点B离地面0点的距离是1m，球落地点A到0点的距离是4m,那么这条抛物线的解析式为_____________.y=-0.04(x-20)2+16y=-x2+x+15.某公园草坪的防护栏是由100段形状相同的抛物线形组成的，为了牢固起见，每段护栏需要间距0.4m加设一根不锈钢的支柱，防护栏的最高点距底部0.5m（如图），则这条防护栏需要不锈钢支柱的总长度至少为（）A.50mB.100mC.160mD.200mC6.河北省赵县的赵州桥的桥拱是抛物线形，水面宽为30米，水面离桥顶的高度是9米，建立如图所示的直角坐标系，你能求出桥拱所在抛物线的函数关系式吗?解:设这条抛物线表示的二次函数为y=ax2.由已知条件可知抛物线经过点(15，-9)，可得-9=a×152解得，a=-因此，桥拱所在抛物线的函数关系式为:y=-x27.如图，一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮，篮球准确落入篮圈，已知篮球运行的路线为抛物线，当篮球运行水平距离为2.5m时，篮球达到最大高度，且最大高度为3.5m，如果篮圈中心距离地面3.05m，那么篮球在该运动员出手时的高度是多少米?解:如图，建立直角坐标系则点B的坐标是(0，3.5)，点C的坐标是(1.5，3.05)点A表示运动员投篮球的出手处设y=ax2+3.5把C(1.5，3.05)代入y=ax2+3.5得3.05=2.25a+3.5，解得a=-0.2∴y=-0.2x2+3.5当x=-2.5时，y=2.25转化回归（二次函数的图象和性质）拱桥问题（实物中的抛物线形问题）建立恰当的直角坐标系①能够将实际距离准确的转化为点的坐标；②选择运算简便的方法.实际问题数学模型转化的关键