《圆的一般方程》人教版高中数学必修二PPT课件（第4.1.2课时）.pptx

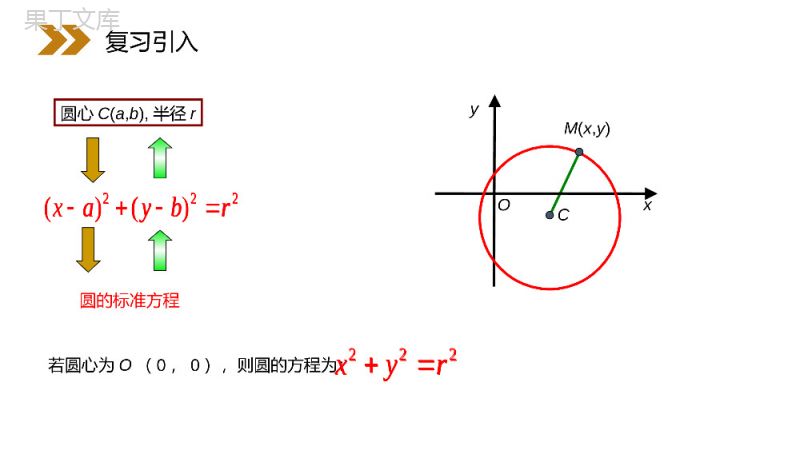
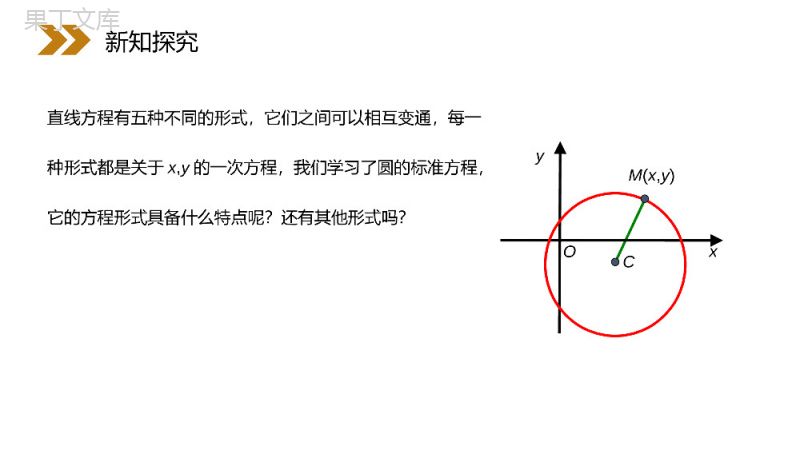
讲解人：办公资源时间：2020.6.1MENTALHEALTHCOUNSELINGPPT4.1.2圆的一般方程第4章圆与方程人教版高中数学必修二1、正确理解圆的一般方程及其特点2、能进行圆的一般方程与标准方程的互化3、回球圆的一般方程及简单的轨迹方程学习目标圆的标准方程xyOCM(x,y)222()()xaybr圆心C(a,b),半径r若圆心为O（0，0），则圆的方程为：222xyr复习引入222()()xaybr222xyr圆心(2,－4)，半径(1)圆(x－2)2+(y+4)2=2(2)圆(x+1)2+(y+2)2=m2圆心(－1,－2)，半径m（m≠0）分别说出下列圆的圆心与半径:新知探究.2直线方程有五种不同的形式，它们之间可以相互变通，每一种形式都是关于x,y的一次方程，我们学习了圆的标准方程，它的方程形式具备什么特点呢？还有其他形式吗？xyOCM(x,y)新知探究222()()xaybr220xyDxEyFxyaxbyabr22222220展开得任何一个圆的方程都是二元二次方程结论：任何一个圆方程可以写成下面形式：圆的一般方程1.圆的标准方程xyDxEyF220问题探究1新知探究222()()xaybr220xyDxEyFxyaxbyabr22222220xyDxEyF2202.是不是任何一个形如方程表示的曲线是圆呢？220xyDxEyFxyxy22(1)2410配方得xyDxEyF220不一定是圆xy22(1)(2)4以（1，-2）为圆心，以2为半径的圆xyxy22(2)2460xy22(1)(2)1配方得不是圆结论：新知探究220xyDxEyFxyxy22(1)2410xyDxEyF220xy22(1)(2)4xyxy22(2)2460xy22(1)(2)1xyDxEyF220DEDEFxy22224224（1）当时，2240DEF表示圆，,22DE-2242DEFr（2）当时，2240DEF表示点,22DE（3）当时，2240DEF不表示任何图形圆心圆的一般方程配方，得新知探究xyDxEyF220DEDEFxy222242242240DEF,22DE-2242DEFr2240DEF,22DE2240DEFxyDxEyF220圆的一般方程，其中DEF2240DEFr2242圆心DE,22-注：圆的一般方程的特点:(2)没有xy项(3)D2+E2-4F＞0(1)x2,y2的系数为1新知探究xyDxEyF220DEF2240DEFr2242DE,22-思考问题:当D=0，E=0或F=0时，圆的位置分别有什么特点？CxOyD=0E=0F=0220xyDxEyFCxyOCxyO新知探究220xyDxEyF(1)x2+y2-2x+4y-4=0(2)2x2+2y2-12x+4y=0(3)x2+2y2-6x+4y-1=0(4)x2+y2-12x+6y+50=0(5)x2+y2-3xy+5x+2y=0是圆心（1，-2）半径3是圆心（3，-1）半径10不是不是不是判断下列方程能否表示圆的方程,若能,写出圆心与半径.练习:新知探究10例1.△ABC的三个顶点的坐标分别A(5,1),B(7,－3)，C(2,－8)，求它的外接圆的方程．xyODA(5,1)B(7,-3)C(2,-8)回顾：方法一：设圆方程为.)()(222rbyax待定系数法方法二：由两条弦的中垂线的交点得到圆心，由圆心到圆上一点得到半径几何法典例展示.)()(222rbyax解：设所求圆的方程为：因为A(5,1),B(7,-3),C(2,-8)都在圆上22222251507(1)7028280DEFDEFDEF4612DEF所求圆的方程为2246120xyxy方法三：待定系数法220xyDxEyF22(2)(3)25xy即待定系数法典例展示22222251507(1)7028280DEFDEFDEF4612DEF2246120xyxy220xyDxEyF22(2)(3)25xy练习1：.)8,0(),0,6(),0,0(的圆的方程求过三点CBA把点A，B，C的坐标代入得方程组0F0662FD0882FE.8,6ED所求圆的方程为：解：设所求圆的方程为：220xyDxEyF22680xyxy课堂练习.)8,0(),0,6(),0,0(的圆的方程求过三点CBA0F0662FD0882FE.8,6ED220xyDxEyF22680xyxy归纳：用待定系数法求圆方程的大致步骤：(1)根据题意，选择标准方程或一般方程。(2)根据条件列出关于a,b,r或D,E,F的方程组；(3)解出a,b,r或D,E,F，代入标准方程或一般方程。课堂练习练习2.证明A(2,2)、B(5,3)、C(3,-1)、D(6,0)四点共圆,并求出此圆的圆心和半径.设所共圆的方程为x2+y2+Dx+Ey+F=0.将A、B、D三点坐标代入得2280,8,53340,2,6360.12.DEFDDEFEDFF解得故过A、B、D三点的圆的方程为x2+y2-8x-2y+12=0.把点C(3,-1)代入方程的左边=9+1-24+2+12=0.课堂练习∴点C在该圆上.∵2D=4,2E=1,∴圆心为(4,1),r=52422FED综上,可得四点共圆，圆心为(4,1),半径为,方程为x2+y2-8x-2y+12=0.2280,8,53340,2,6360.12.DEFDDEFEDFF解得∴点C在该圆上.∵2D=4,2E=1,∴圆心为(4,1),r=52422FED将方程配方，得(x+1)2+y2=4.练习3：解析：在给定的坐标系中，设M(x，y)是曲线上的任意一点，点M在曲线上的条件是21MAMO由两点的距离公式，上式用坐标表示为两边平方并化简，得曲线方程x2+y2+2x-3=0.∴所求曲线是圆心为C(-1，0)，半径为2的圆.已知一曲线是与两个定点O(0，0)、A(3，0)距离的比为的点的轨迹，求出曲线的轨迹.21222212(3)xyxy课堂练习222212(3)xyxy一、基本知识1.圆的标准方程.2.圆的一般方程.3.求圆的方程的方法：①待定系数法；②代入法（几何法）.222)()(rbyax（圆心C(a,b),半径r）220xyDxEyF，其中DEF2240DEFr2242DE,22-课堂总结222)()(rbyax220xyDxEyFDEF2240DEFr2242DE,22-几何方法求圆心坐标（两条直线的交点）（常用弦的中垂线）求半径（圆心到圆上一点距离）写出圆的标准方程待定系数法列关于a，b，r（或D，E，F）的方程组解出a，b，r（或D，E，F），写出标准方程（或一般方程）22222(-)(-)(0)xaybrxyDxEyF设方程为或课堂总结22222(-)(-)(0)xaybrxyDxEyF设方程为或感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明讲解人：办公资源时间：2020.6.1MENTALHEALTHCOUNSELINGPPT感谢你的聆听第4章圆与方程人教版高中数学必修二