极坐标下的二重积分,极坐标下的二重积分交换积分次序
本作品内容为极坐标下的二重积分,格式为 docx ,大小 3169 KB ,页数为 1页

('极坐标下的二重积分极坐标下的二重积分是数学中的一个重要概念,它是对极坐标系中的曲线或曲面进行积分的一种方法。在极坐标系中,每个点都由一个极径和一个极角确定,因此可以用极坐标系来描述一些复杂的曲线和曲面。二重积分是对平面区域上的函数进行积分的一种方法,它可以用来计算平面区域上的面积、质心、重心等物理量。在极坐标系中,二重积分的计算方法与直角坐标系中的二重积分有所不同,需要用到极坐标系下的面积元素和积分限。对于一个在极坐标系下的平面区域,可以将其分成若干个小扇形区域,每个小扇形区域的面积可以表示为dA=rdrdθ,其中r表示极径,θ表示极角。因此,极坐标系下的二重积分可以表示为:∬f(r,θ)dA=∫∫f(r,θ)rdrdθ其中f(r,θ)表示在极坐标系下的函数,r和θ分别表示积分变量的极径和极角。积分限的选择也需要根据具体情况来确定,通常是将平面区域分成若干个小扇形区域,然后对每个小扇形区域进行积分,最后将所有小扇形区域的积分结果相加得到整个平面区域的积分结果。极坐标系下的二重积分在数学和物理学中都有广泛的应用,例如在计算圆形、椭圆形、心形等曲线的面积、质心、重心等物理量时都可以使用极坐标系下的二重积分。此外,在计算电场、磁场等物理量时也常常需要用到极坐标系下的二重积分。极坐标系下的二重积分是数学中的一个重要概念,它可以用来计算平面区域上的各种物理量,具有广泛的应用价值。对于学习数学和物理学的人来说,掌握极坐标系下的二重积分是非常重要的。',)
提供极坐标下的二重积分,极坐标下的二重积分交换积分次序会员下载,编号:1700758214,格式为 docx,文件大小为1页,请使用软件:wps,office word 进行编辑,PPT模板中文字,图片,动画效果均可修改,PPT模板下载后图片无水印,更多精品PPT素材下载尽在某某PPT网。所有作品均是用户自行上传分享并拥有版权或使用权,仅供网友学习交流,未经上传用户书面授权,请勿作他用。若您的权利被侵害,请联系963098962@qq.com进行删除处理。

 下载
下载 下载
下载 下载
下载 下载
下载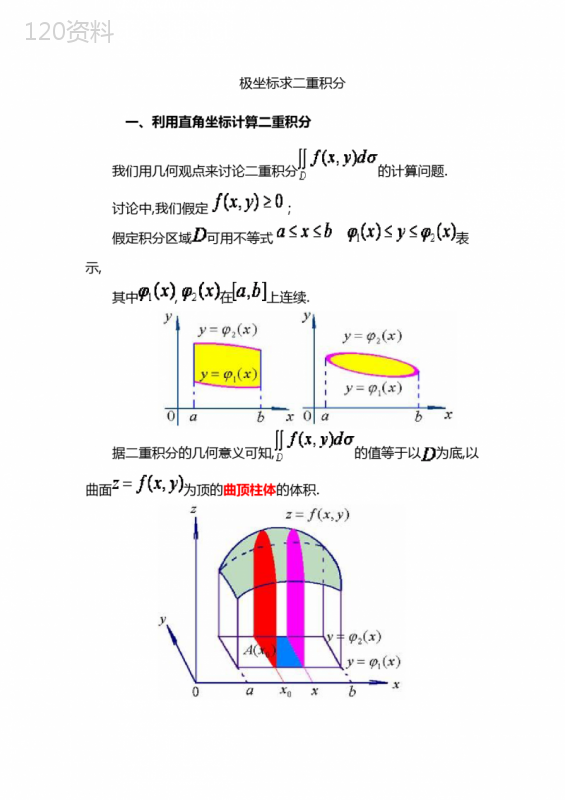 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载