高数二重积分习题解答,高数二重积分例题详解
本作品内容为高数二重积分习题解答,格式为 docx ,大小 967090 KB ,页数为 37页

("..第9章重积分及其应用1.用二重积分表示下列立体的体积:(1)上半球体:;(2)由抛物面,柱面x2+y2=1及xOy平面所围成的空间立体解答:(1);(2)所属章节:第九章第一节难度:一级2.根据二重积分的几何意义,确定下列积分的值:(1),其中D为;(2),其中D为解答:(1);(2)所属章节:第九章第一节难度:一级3.一带电薄板位于xOy平面上,占有闭区域D,薄板上电荷分布的面密度为,且在D上连续,试用二重积分表示该板上的全部电荷Q.解答:所属章节:第九章第一节难度:一级4.将一平面薄板铅直浸没于水中,取x轴铅直向下,y轴位于水平面上,并设薄板占有xOy平面上的闭区域D,试用二重积分表示薄板的一侧所受到的水压力’...解答:所属章节:第九章第一节难度:一级5.利用二重积分性质,比较下列各组二重积分的大小(1)与,其中D是由x轴,y轴及直线x+y=1所围成的区域;(2)与,其中D是矩形区域:0≤x≤1,0≤y≤1;(3)与,其中D是任一平面有界闭区域;(4)与,其中D是矩形区域:–1≤x≤0,0≤y≤1;解答:(1)在区域D内部,,所以I1>I2;(2)在区域D内部,,故,所以I1>I2;?(3)由于,所以I1
提供高数二重积分习题解答,高数二重积分例题详解会员下载,编号:1700759016,格式为 docx,文件大小为37页,请使用软件:wps,office word 进行编辑,PPT模板中文字,图片,动画效果均可修改,PPT模板下载后图片无水印,更多精品PPT素材下载尽在某某PPT网。所有作品均是用户自行上传分享并拥有版权或使用权,仅供网友学习交流,未经上传用户书面授权,请勿作他用。若您的权利被侵害,请联系963098962@qq.com进行删除处理。

 下载
下载 下载
下载 下载
下载 下载
下载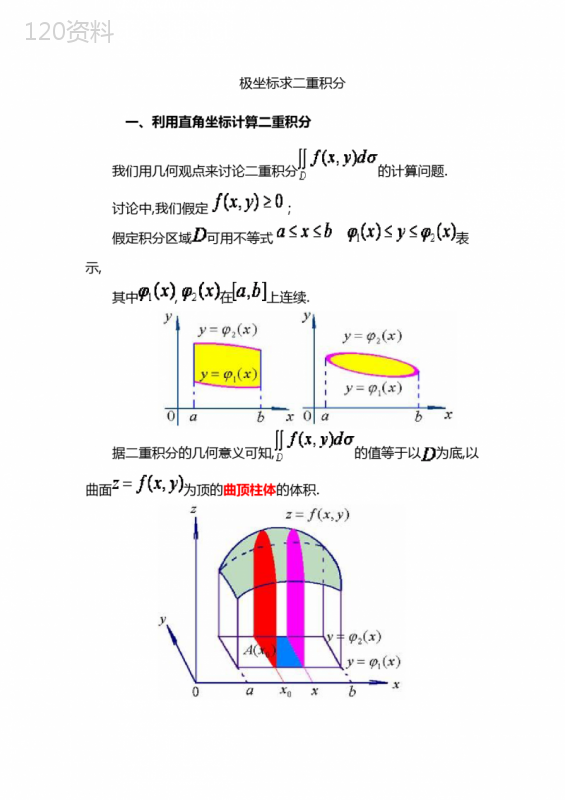 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载