实际问题与二次函数复习(1),实际问题与二次函数教学视频

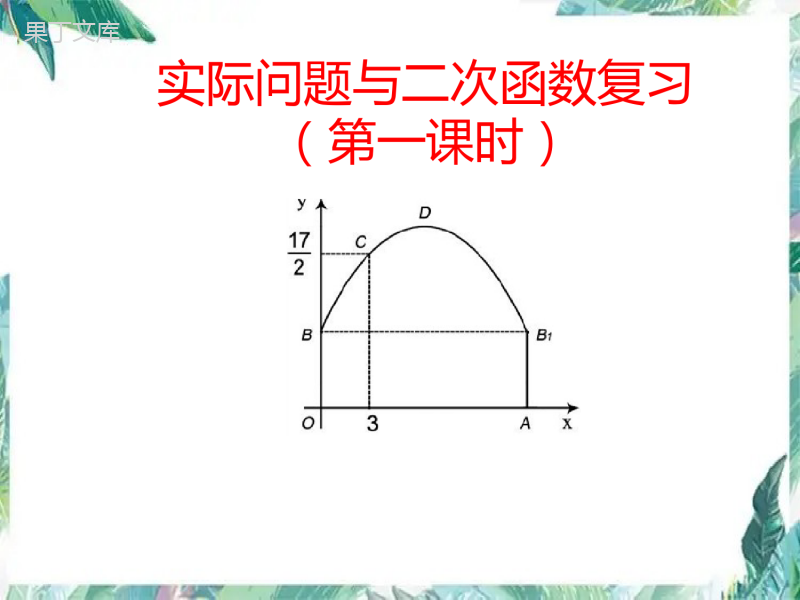
实际问题与二次函数复习（第一课时）基础检测1.［2019•合肥三十八中一模］已知二次函数y=x2－4x＋5,则该函数的顶点坐标为().A.(－2,－1）B.(2,1)C.(2,－1）D.(－2,1)2.［2019•河北沧州十三中二模］一小球被抛出后，距离地面的高度h(m)和飞行时间t(s)满足下面函数关系式h=-5(t－1)2＋6,则小球距离地面的最大高度是()A.1mB.5mC.6mD.7mBC3.［2019•湖北武汉武珞路中学二模］飞机着陆后滑行的距离s(单位：m)与滑行的时间t(单位：s)之间的函数关系式是s=60t－1.5t2.飞机着陆后滑行______s才能停下来。20例［2015·青岛］如图隧道的截面由抛物线和长方形构成，长方形的长是12m，宽是4m．按照图中所示的直角坐标系，抛物线可以用cbxxy261表示，且抛物线上的点C到OB的水平距离为3m，到地面OA的距离为217m。（1）求抛物线的函数关系式，并计算出拱顶D到地面OA的距离；（2）一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向车道，那么这辆货车能否安全通过？（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？例题精析解：（1）由题意知，点)217,3(),4,0(CB在抛物线上所以cbc39612174，解得42cb，所以42612xxy.则y=－61(x－6)2＋10.所以，当x=6时，10最大y.答：42612xxy，拱顶D到地面OA的距离为10米。（2）由题意知，车最外侧与地面OA的交点为（2,0）（或（10,0））当)10(2xx或时，6322＞y，所以可以通过.（3）令8y，即842612xx，可得024122xx，解得326,32621xx.3421xx。答：两排灯的水平距离最小是34米。［2014·成都］在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设xABm.（1）若花园的面积为1922m,求x的值；（2）若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），求花园面积S的最大值.巩固拓展解：（1）∵AB=xm,则BC=（28－x）m,∴x（28－x）=192.解得x1=12,x2=16.答：x的值为12m或16m.(2)由题意，得S=x（28－x）=－x2+28x=－(x－14)2+196.∵P处有一棵树与墙CD,AB的距离分别是15m和6m,28－x≥15,∴解得6≤x≤13.x≥6,∴x=13时，S取最大值为S=－(13－14)2+196=195.答：花园面积S的最大值为195m2.总结反思通过本节课的复习，谈谈你的收获和体会？分层作业1.必做题：［2015•丹东］某商店购进一种商品，每件商品进价30元。试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下：x30323436y40363228(1)已知y与x满足一次函数关系，根据上表，求出y与x之间的函数关系式（不写出自变量x的取值范围）；(2)如果商店销售这种商品，每天要获得150元利润，那么每件商品的销售价应定为多少元？(3)设该商店每天销售这种商品所获利润为w（元），求出w与x之间的关系式，并求出每件商品销售价定为多少元时利润最大？2.选做题：［2015•合肥十五中二模］如图,半径为2的半圆内接等腰梯形ABCD，它的下底AB是圆的直径，上底CD的端点在圆周上，则该梯形周长的最大值是多少？新语录成功新捷径：成功就是1％的灵感加99％的远离手机.——摘自2015.19《青年文摘》再见！