三角形的内角,三角形的内角和是多少度

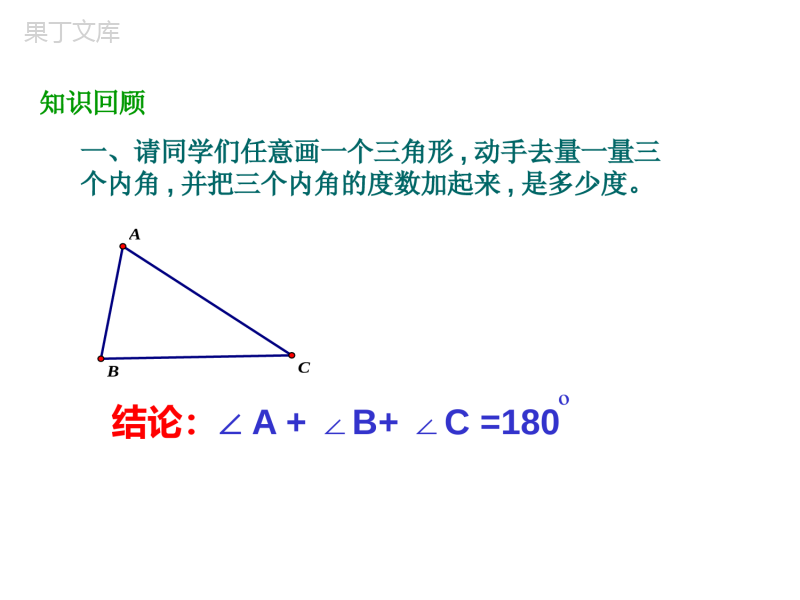
请拿出你的课本、导学案，双色笔，练习本，还有你的激情！温馨提示课前赠言：提出问题比解决问题更重要！11.2与三角形有关的角11.2.1三角形的内角11.2与三角形有关的角1.掌握三角形的内角和定理，了解直角三角形两个锐角的关系，掌握直角三角形的判定.2.会用平行线的性质与平角的定义证明三角形内角和等于180°.3.能运用三角形的内角和定理进行简单的证明或计算.学习目标导学案反馈目标导向：通过问题反馈，进一步明确存在的问题，做到有的放矢！存在的问题：1.内角和等于180°的证明过程2.内角和的使用3.几何语言的书写知识回顾结论：∠A+B+C∠∠=180º一、请同学们任意画一个三角形,动手去量一量三个内角,并把三个内角的度数加起来,是多少度。ABC问题探究问：通过这样拼接，你发现了什么，三角形的三个内角和是多少?º结论：三角形三个内角的和等于180°二、任意画一个三角形，把三角形三个角剪下来，拼在一起你会发现什么？3212132123321定理：三角形三个内角的和是180°从刚才拼角的过程你能想出证明的办法吗分析：1、平角2、两直线平行，同旁内角互补。证明:过点A作EFB∥C，已知：△ABC.三角形的内角和等于1800.CBAFE∵EFBC∥∴∠B=∠EAB(两直线平行,内错角相等)同理∠C=∠FAC又∵∠EAB+∠FAC+∠BAC=180°(平角定义)∴∠B+∠C+∠BAC=180°（等量代换）证明：∠A+∠B+∠C=180°.证法一证明:延长BC到D，过C作CEBA∥，三角形的内角和等于1800.证法二已知：△ABC.CBA证明：∠A+∠B+∠C=180°.21EDABC∴∠A=∠1(两直线平行，内错角相等)∠B=∠2(两直线平行，同位角相等)又∵∠1+∠2+∠ACB=180°（平角定义）∴∠A+∠B+∠ACB=180°（等量代换）证明:过点C作CDAB∥，∴∠A=∠1(两直线平行,内错角相等)∠B+∠BCA+∠1=180°(两直线平行,同旁内角互补)∴∠B+∠A+∠BCA=180°已知：△ABC.CBA证明：∠A+∠B+∠C=180°.三角形的内角和等于1800.证法三1DABC1.求出下列各图中的x值．4070xx°x°x°2x°x°25°45°20°x°x=70x=60x=30x=50②在△ABC中，∠A:∠B:∠C=1:2:3，则△ABC是_________三角形.练一练：①在△ABC中，∠A=35°，∠B=43°，则∠C=.③在△ABC中，∠A=∠B+10°,∠C=∠A+10°,则∠A=，∠B=，∠C=.102°直角60°50°70°思路总结为了证明三个角的和为180°,利用逆向思考的方法,把问题转化为一个平角,同旁内角互补,或者其它方法.这种转化思想是数学中的常用方法.在这里，为了证明的需要，在原来的图形上添画的线叫做辅助线.在几何里，辅助线通常画成虚线.百家争鸣，百花齐放——成长与精彩属于我们具体要求：利用三角形内角和解决实际度数问题。展示要求:(1)书写认真、步骤规范，用好双色笔。(2)总结题目的规律、方法，注重多角度考虑问题。(3)先组内讨论，再组间学习；展示题目展示小组对点巩固11对点巩固22对点巩固33要求（1）书面展示要分层次，书写要认真、规范。⑵非展示同学巩固基础知识、整理落实学案，做好拓展。把典型的题目整理到典型题集上，不浪费一分钟，小组长做好安排和检查。1.面向同学，声音洪亮，语言精炼，自然大方；2.点评时注重对题目思路和方法的分析，点明注意事项，并总结方法和规律；3.其他同学要求极度专注，积极质疑、追问、解答。点评题目点评小组对点巩固14对点巩固25对点巩固36例1：在△ABC中,∠A=80°,∠B=∠C,求∠C的度数。ABC例2：已知三角形三个内角的度数之比为1:3:5，求这三个内角的度数。例3：在△ABC中，∠A的度数是∠B的度数的3倍，∠C比∠B大15°，求∠A，∠B，∠C的度数.解:设∠B为x°，则∠A为(3x)°，∠C为(x＋15)°，从而有3x＋x＋(x＋15)＝180.解得x＝33.所以3x＝99，x＋15＝48.答：∠A，∠B，∠C的度数分别为99°，33°，48°.几何问题借助方程来解.这是一个重要的数学思想.【变式题】如图，B岛在A岛的南偏西40°方向，C岛在A岛的南偏东15°方向，C岛在B岛的北偏东80°方向，求从C岛看A，B两岛的视角∠ACB的度数.解：如图，由题意得BE∥AD,∠BAD=40°，∠CAD=15°，∠EBC=80°，∴∠EBA=∠BAD=40°，∠BAC=40°+15°=55°,∴∠CBA=∠EBC-∠EBA=80°-40°=40°，∴∠ACB=180°-∠BAC-∠ABC=180°-55°-40°=85°．DE2.如图，则∠1+2+3+4=___________.∠∠∠BACD4132E40°（280°三角形的内角和定理证明了解添加辅助线的方法及其目的内容三角形内角和等于180°定理应用直角三角形：直角所对的边叫两个锐角所对的边叫斜边直角边表示方法：Rt△ABC直角边直角边斜边ABC∠A+∠B=90º性质：课堂小结