2022-2023学年湘教版数学七年级上册同步多媒体教学-第1章-有理数的乘法第1课时

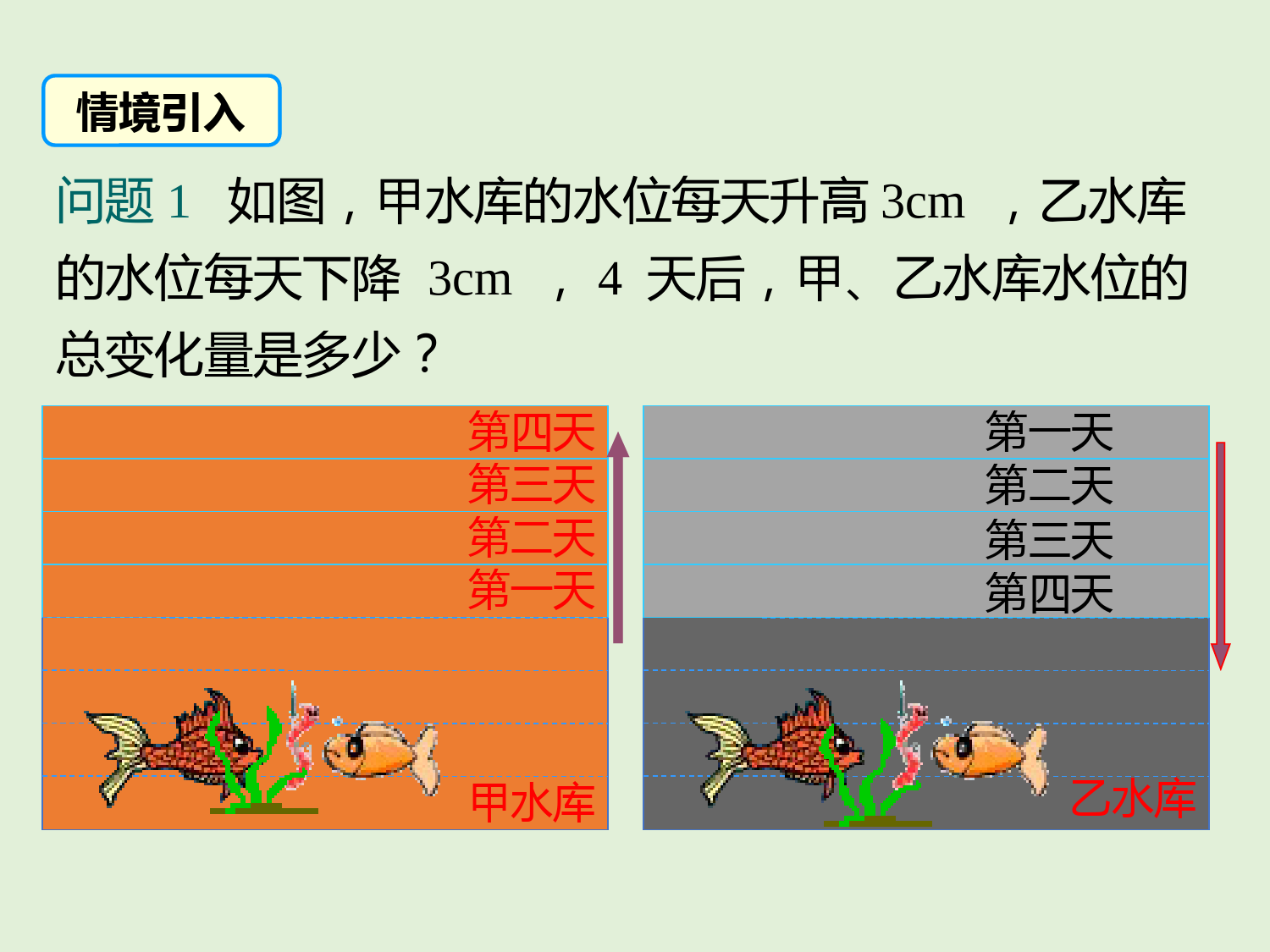
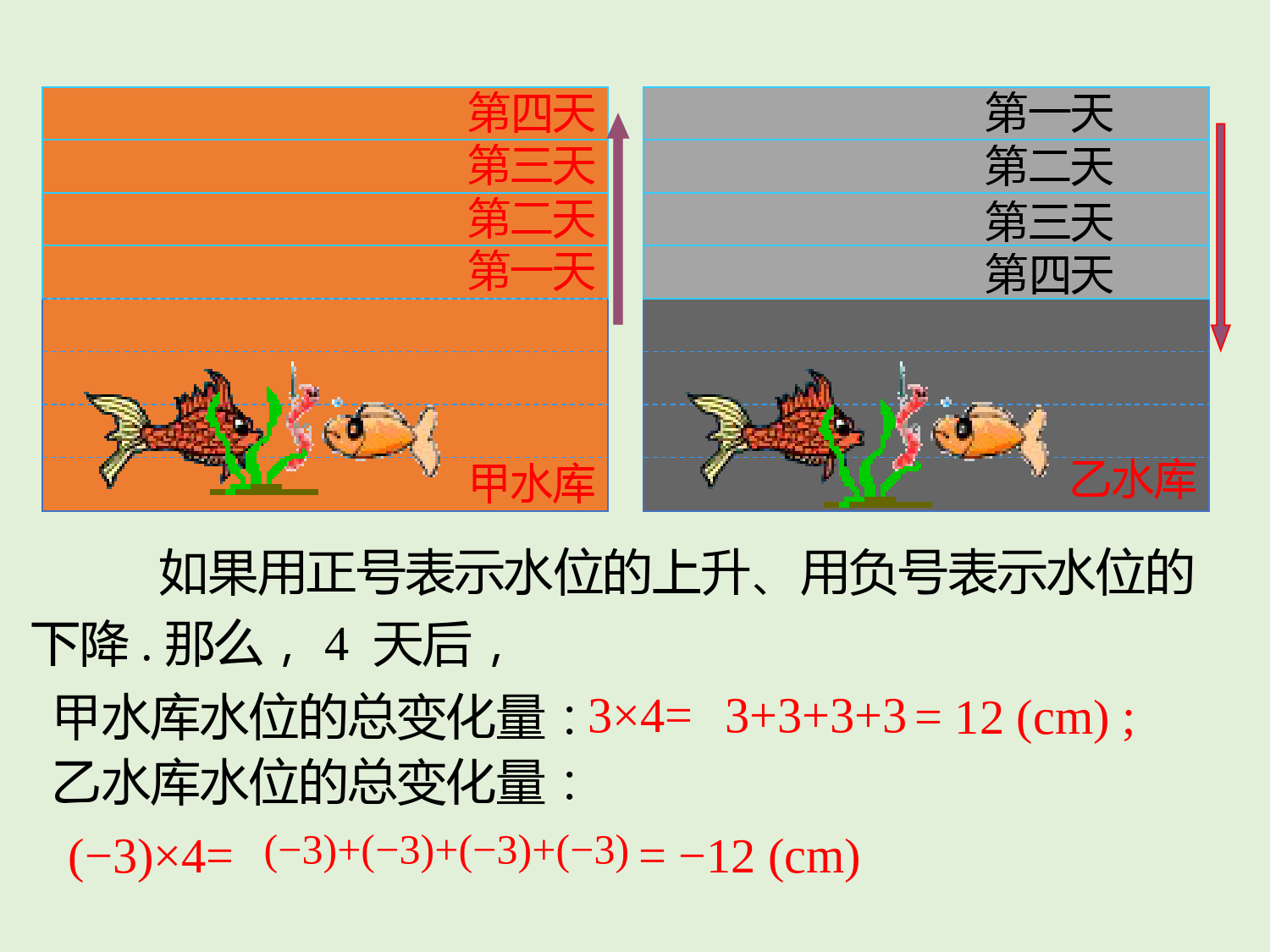
第一章有理数1.5.1有理数的乘法学习目标1.掌握有理数的乘法法则并能进行熟练地运算.(重点）2.掌握多个有理数相乘的积的符号法则.（难点）甲水库第一天乙水库第二天第三天第四天第一天第二天第三天第四天问题1如图，甲水库的水位每天升高3cm，乙水库的水位每天下降3cm，4天后，甲、乙水库水位的总变化量是多少？情境引入甲水库第一天乙水库第二天第三天第四天第一天第二天第三天第四天如果用正号表示水位的上升、用负号表示水位的下降.那么，4天后，甲水库水位的总变化量：乙水库水位的总变化量：3+3+3+33×4==12(cm);(−3)×4==−12(cm)(−3)+(−3)+(−3)+(−3)(−3)×4=(−3)+(−3)+(−3)+(−3)=−12(−3)×3=_____________=_____,(−3)×2=_____________=_____,(−3)×1=_____,(−3)×0=_____.−9−6−30类比前面得到的两个式子，填空：(−3)+(−3)+(−3)(−3)+(−3)3×4=3+3+3+3=12如图,一只蜗牛沿直线l爬行，它现在的位置在l上的点O．lＯ1.如果一只蜗牛向右爬行2cm记为+2cm，那么向左爬行2cm应该记为.2.如果3分钟以后记为+3分钟，那么3分钟以前应该记为.-2cm-3分钟有理数的乘法运算一合作探究探究12O264l结果：3分钟后在l上点O边cm处表示：.右6（+2）×（+3）=6(1)如果蜗牛一直以每分钟2cm的速度向右爬行，3分钟后它在什么位置？规定：向左为负，向右为正．现在前为负，现在后为正．(2)如果蜗牛一直以每分钟2cm的速度向左爬行，3分钟后它在什么位置？探究2-6-4O-22l结果：3分钟后在l上点O边cm处左6表示:.（-2）×（+3）＝－62×3=6（-2）×3=-6一个因数换成相反数积是原来的积的相反数发现：两数相乘，把一个因数换成它的相反数，所得的积是原来积的相反数.议一议2×3=62×(-3)=-6(-2)×（-3）=6相反数相反数相反数相反数猜一猜(3)如果蜗牛一直以每分钟2cm的速度向右爬行，3分钟前它在什么位置？探究32-6-4O-22l结果：3分钟前在l上点O边cm处表示：.（+2）×（-3）＝－6左6验证了前面猜想(4)如果蜗牛一直以每分钟2cm的速度向左爬行，3分钟前它在什么位置？探究42O264-2l结果：3钟分前在l上点O边cm处.右6表示：.（-2）×（-3）＝＋6分组讨论：（1）2×3=6（2）（-2）×（-3）=6（3）（-2）×3=-6（4）2×（-3）=-6正数×正数负数×负数负数×正数=正数=正数=负数=负数正数×负数发现：两数相乘，同号得正，异号得负，并把绝对值相乘.结果:都是仍在原处，即结果都是.若用式子表达：探究5（5）原地不动或运动了零次，结果是什么？0×3=0；0×(－3)=0；2×0=0；(－2)×0=0．零Ｏ发现：任何数与0相乘，积仍为0.两数相乘，综合如下：（1）2×3=6（2）（-2）×（-3）=6（3）（-2）×3=-6（4）2×（-3）=-6（5）3×0=0，0×3=0（6）（-3）×0=0，0×（-2）=0同号相乘,积为正数异号相乘,积为负数如果有一个因数是0时，所得的积还是0.两数的符号特征积的符号积的绝对值同号异号一个因数为0有理数乘法法则:+-绝对值相乘得0先定符号,再定绝对值!归纳总结讨论:(1)若a＜0,b＞0,则ab____0;(2)若a＜0,b＜0,则ab____0;(3)若ab＞0,则a、b应满足什么条件？(4)若ab＜0,则a、b应满足什么条件？＜＞a、b同号a、b异号先确定下列积的符号，再计算结果：（1）5×（-3）（2）（-4）×6（3）（-7）×（-9）（4）0.5×0.7积的符号为负积的符号为负积的符号为正积的符号为正=-15=-24=63=0.35做一做例1计算：(1)3.5×(-2)；(2)(3)(4)(-0.57)×0.32;8913;3解：(1)3.5×(-2)=-(3.5×2)=-7；323212;898912113331;33(4)(-0.57)×0=0.总结：有理数乘法的求解步骤:先确定积的符号；再确定积的绝对值.例2用正负数表示气温的变化量，上升为正，下降为负.登山队攀登一座山峰，每登高1km，气温的变化量为-6℃，攀登3km后，气温有什么变化？解：（-6）×3=-18答：气温下降18.℃有理数的乘法的应用二【变式】气象观测统计资料表明，在一般情况下，高度每上升1km,气温下降6.℃已知甲地现在地面气温为21℃，求甲地上空9km处的气温大约是多少.解：（-6）×9=-54（℃）；21+（-54）=-33（℃）.答：甲地上空9km处的气温大约为-33℃.被乘数乘数积的符号积的绝对值结果－57156－30－64－251.填空：－35－35+9090+180180－100－1002.若ab>0，则必有()A.a>0，b>0B.a<0，b<0C.a>0，b<0D.a>0，b>0或a<0,b<03.若ab=0，则一定有()A.a=b=0B.a,b至少有一个为0C.a=0D.a,b最多有一个为0DB解：112-4-(2.54)-10;2（）（）75751);102110216（2）（-（-）=55453(-10.8)-2;27527（）（）112（）2（-4）；75)1021（2）（-（-）；527（3）(-10.8)（-）；13)0.2（4）（-4.计算：13)00.2（4）（-5.商店降价销售某种商品，每件降5元，售出60件后，与按原价销售同样数量的商品相比，销售额有什么变化？解：（-5）×60=-300(元)答：销售额减少300元.有理数乘法法则一般法则应用两数相乘，同号得正，异号得负，并把绝对值相乘.特殊任何数同0相乘，都得0.谢谢观看