11.1.2三角形的高、中线与角平分线

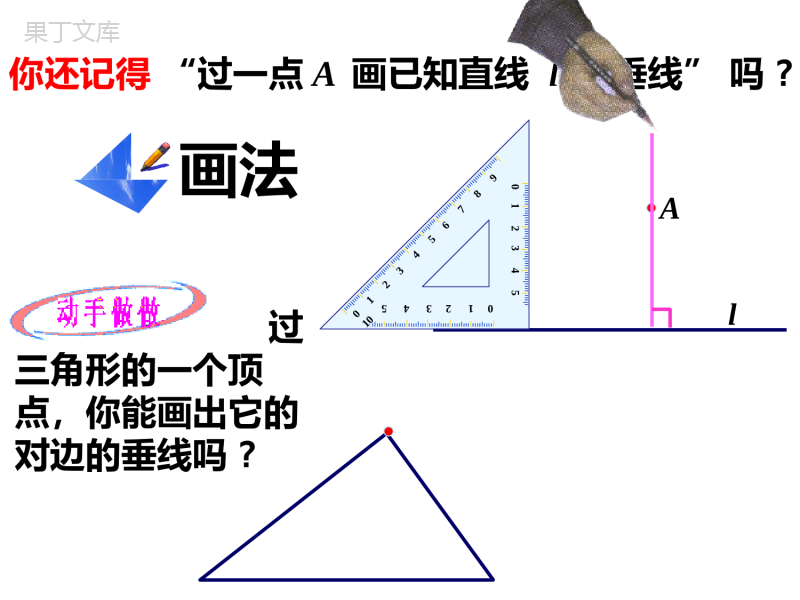
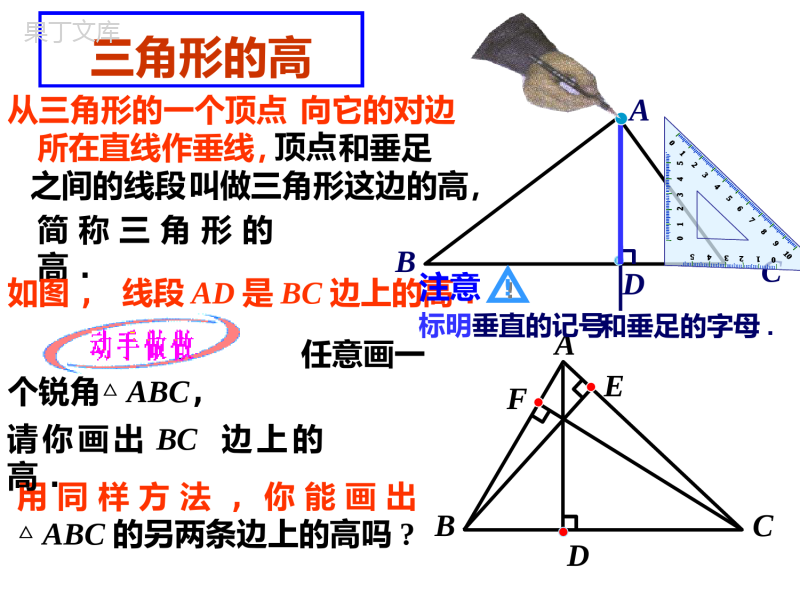
11.1.2三角形的高、中线与角平分线人教版八年级(上)第十一章三角形三角形定义表示方法三边关系定理分类按边分类按角分类复习你还记得上一节课吗？2.线段的中点：3.角平分线：1.垂线：一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线.把一条线段分成两条相等的线段的点.当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线.相关知识回顾你还记得“过一点A画已知直线l的垂线”吗?画法012345678910012345012345过三角形的一个顶点，你能画出它的对边的垂线吗?BACAl三角形的高A从三角形的一个顶点BC向它的对边所在直线作垂线，顶点和垂足D之间的线段叫做三角形这边的高，简称三角形的高.如图,线段AD是BC边上的高.任意画一个锐角△ABC,用同样方法,你能画出△ABC的另两条边上的高吗?ABC请你画出BC边上的高.DEF和垂足的字母.注意!标明垂直的记号如图,(1)(2)和(3)中的三个三角形有什么不同?怎样画出BC边上的高?你能说出其中的规律吗?DDDODABC┐EFPRQ三条高交于三角形内一点。三条高交于直角顶点三条高的延长线交于三角形外部一点1.分别指出图中△ABC的三条高。DEABCFAB边上的高是;CEBC边上的高是;ADCA边上的高是;BF2、如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（）A.锐角三角形B.直角三角形C.钝角三角形D.锐角三角形B三角形的中线在三角形中,连结一个顶点和它对边中点的线段叫做这个三角形这边的中线.如图,△ABC,如何取BC边的中点?用同样方法,你能画出△ABC的另两条边上的中线吗?DEF你有什么发现?如图,三角形的三条中线相交于一点,三角形三条中线的交点叫做三角形的重心.2_____,______,1_____.2ABBDAE如图,AD、BE、CF是△ABC的三条中线，则交点O就是△ABC的重心.则2_____,______,1_____.2ABBDAEAFCDAC1.如图,AD是△ABC的中线，△ABD的面积S1与△ADC的面积S2有什么数量关系?2.如图,△ABC的三条中线AD、BE、CF交于点O，图中6个小三角形的面积有何关系?ES1=S2结论:三角形的一条中线把三角形分成面积相等的两个三角形.三角形的角平分线叫做三角形的角平分线.在三角形中，一个内角的角平分线与它的对边相交，这个角的顶点与交点之间的线段,如图,△ABC,如何画∠BAC的角平分线?D图中线段AD叫做△ABC的角平分线.用同样方法,你能画出△ABC的其他的角平分线吗?你有什么发现?如图,AD、BE、CF是△ABC的三条角平分线,则1______,13_____,22____.ACB1______,13_____,22____.ACB2ABC4小结本节课,你有什么收获?说一说.三角形的高三角形的中线三角形的角平分线从定义,位置,交点等方面说说它们的异同.1.以下是四位同学在钝角三角形ABC中画BC边上的高，其中画法正确的是（）练习BABCD2.小华在电话中问小明：“已知一个三角形三边长分别是4，9，12，如何求这个三角形的面积？”小明提示说：“可通过作最长边上的高来求解．”小华根据小明的提示作出的图形正确的是（）ABCDC4.如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（）A.锐角三角形B.直角三角形B3.可以把一个三角形分成面积相等的两部分的线段是（）A.三角形的高B．三角形的角平分线C.三角形的中线D．无法确定CFEDCBA5.如图，在ΔABC中，AE是中线，AD是角平分线，AF是高。填空：（1）BE==½；（2）∠BAD==½；（3）∠AFB==90°；CEBC∠CAD∠BAC∠AFC6.如图1所示,在△ABC中,ACB=90°,∠把△ABC沿直线AC翻折180°,使点B落在点B′的位置,则线段AC具有性质()A.是边BB′上的中线B.是边BB′上的高C.是∠BAB′的角平分线D.以上三种性质合一DB'CBA7.如图,△ABC中,∠B=90°.D是BC上一点,AB=3,BD=2.(1)若BD=DC,则△ADC的面积为_______;(2)若BD=2DC,则△ADC的面积为_______.332填空题:(每小题3分,共12分)1.三角形的三条中线交于一点,这一点在_______,三角形的三条角平分线交于一点,这一点在__________,三角形的三条高线所在直线交于一点,这一点在_____.2.等腰三角形的高线、角平分线、中线的总条数为_______.三角形内三角形内三角形内或外或直角顶点上7如图,△ABC中,BD是角平分线,DE∥BC.求证∠1=2.∠已知AE是∠BAC的平分线，∠1=D∠，求证：∠1=2∠如图，已知AD，AE分别是△ABC的高和中线，AD=5cm，EC=2cm。求△ABC的面积。ABEDC如图，在△ABC中，CEAB,ADBC,⊥⊥且AB=3，BC=6，CE=4，求AD的长度。ABCDE18.如图，EABDC如图，△ABC中，AE，CD分别为△ABC的高，若AE=3cm，CD=5cm，AB=4cm，求BC的长。已知在三角形ABC中，AB=AC，D为BC上一点，DEAB⊥于E，DFAC⊥于F，BGAC⊥，求证：BG=DE+DFABCEGF如图，已知在RtABC△中，∠ABC=90°，点D沿BC自B向C运动（点D与点B、C不重合），作BEAD⊥于E，CFAD⊥于F，则BE+CF的值（）A．不变B．增大C．减小D．先变大再变小如图，BM是△ABC的中线，AB=6，BC=8，则△MBC的周长与△ABM的周长相差多少？BAMC如图所示，CD为△ABC的AB边上的中线，△BCD的周长比△ACD的周长大3cm，BC=8cm，求边AC的长。如图。已知AD，AE，分别是△ABC的高和中线，AB=6cm,AC=8cm,BC=10cm,CAB=90°∠。问题：试求（1）AD的长度；（2）△ABE的面积；（3）△ACE和△ABE周长的差ACBDEFEDCBA,,,,ABCDEFBCADCE如图所示，在中，已知点分别为边的中点24,ABCScmS阴影且则等于多少？19.,,,,ABCDEFBCADCE如图所示，在中，已知点分别为边的中点24,ABCScmS阴影且则等于多少？如图SABC=1△，且D是BC的中点，AE：EB=1：2，求△ADE的面积如图所示，SABC=1△，若SBDE=△SDEC=△SACE△，求△ADE的面积。如图，D、E分别是△ABC边AB、BC上的点，AD=2BD，BE=CE，设△ADF的面积为S1，△CEF的面积为S2，若SABC=9△，求S1-S2的值8.在△ＡＢＣ中，ＡＢ＝ＡＣ，ＡＣ上的中线ＢＤ把三角形的周长分为２１㎝和１２㎝两部分，求三角形各边长。解：如图，设ＡB＝AＣ＝ｘ，则（１）若ＡＢ+ＡＤ＝２１，即ｘ＋１／２ｘ＝２１，解的ｘ＝１４，即ＡＢ＝ＡＣ＝１４，从而ＤＣ＝７，于是ＢＣ＝５。ＡＢＣＤ（２）若ＡＢ＋ＡＤ＝１２，即ｘ＋１／２ｘ＝１２，解的ｘ＝８，即ＡＢ＝ＡＣ＝８，从而ＤＣ＝４，于是ＢＣ＝１７，此时ＡＢ＋ＡＣ﹤ＢＣ，不能构成三角形。综上所述，所求的三角形的边长分别为１４㎝１４㎝和５㎝。作业：在△ＡＢＣ中，ＡＢ＝ＡＣ，ＡＣ上的中线ＢＤ把三角形的周长分为6㎝和15㎝两部分，求三角形各边长。ＡＢＣＤ1.作业课本8页3题,8题.9题.2.课外作业4题(写在课本上)