第27课时-平行四边形,平行四边形的判定几课时

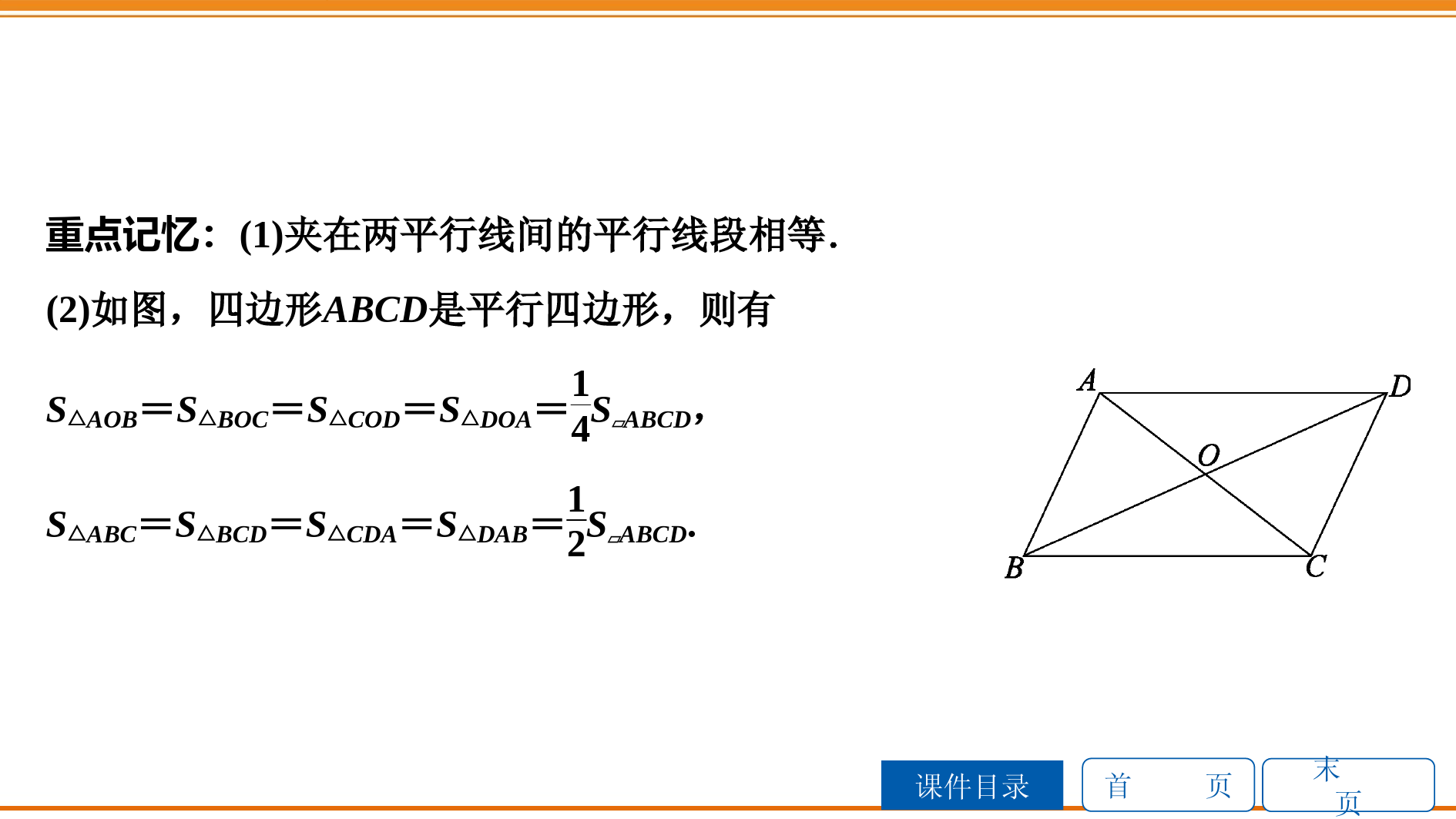
首页课件目录末页第二部分图形与几何第八章四边形考点管理中考再现课时作业归类探究第27课时平行四边形首页课件目录末页考点管理1．平行四边形的概念定义：两组对边分别的四边形叫做平行四边形．2．平行四边形的性质性质：(1)平行四边形的对边；(2)平行四边形的对角；(3)平行四边形的对角线．注意：平行四边形是以对角线的交点为对称中心的中心对称图形，但不一定是轴对称图形．平行平行且相等相等互相平分首页课件目录末页3．平行四边形的判定判定：(1)两组对边分别的四边形是平行四边形；(2)对角线的四边形是平行四边形；(3)两组对角分别的四边形是平行四边形；(4)一组对边的四边形是平行四边形．注意：(1)平行四边形的定义既可以作为性质，又可以作为判定；(2)一组对边平行，一组对角相等的四边形是平行四边形；(3)一组对边平行，另一组对边相等的四边形不一定是平行四边形，有可能是等腰梯形．平行或相等互相平分相等平行且相等首页课件目录末页重点记忆：(1)夹在两平行线间的平行线段相等．(2)如图，四边形ABCD是平行四边形，则有S△AOB＝S△BOC＝S△COD＝S△DOA＝14S▱ABCD，S△ABC＝S△BCD＝S△CDA＝S△DAB＝12S▱ABCD.首页课件目录末页4．两平行线间的距离定义：两条平行线中一条直线上任意一点到另一条直线的距离叫做两条平行线间的距离．首页课件目录末页中考再现1．[2019·永州]如图，四边形ABCD的对角线相交于点O，且点O是BD的中点，若AB＝AD＝5，BD＝8，∠ABD＝∠CDB，则四边形ABCD的面积为()A．40B.24C．20D.15B首页课件目录末页【解析】∵∠ABD＝∠CDB，∴AB∥CD.∵O是BD的中点，∴BO＝DO.又∵∠AOB＝∠COD，∴△AOB≌△COD(ASA)，∴AB＝CD.又∵AB∥CD，∴四边形ABCD是平行四边形．∵AB＝AD，∴四边形ABCD是菱形．∴AC⊥BD.首页课件目录末页在Rt△ABO中，BO＝12BD＝4，AO＝AB2－BO2＝52－42＝3.∴AC＝2AO＝6.∴S四边形ABCD＝12AC·BD＝12×6×8＝24.故选B.首页课件目录末页2．[2019·岳阳]如图，▱ABCD中，AB＝2，AD＝4，对角线AC，BD相交于点O，且E，F，G，H分别是AO，BO，CO，DO的中点，则下列说法正确的是()BA．EH＝HGB．四边形EFGH是平行四边形C．AC⊥BDD．△ABO的面积是△EFO的面积的2倍首页课件目录末页【解析】E，F，G，H分别是AO，BO，CO，DO的中点，∴EH∥AD且EH＝12AD，FG∥BC且FG＝12BC.在▱ABCD中，AD∥BC且AD＝BC，∴EH∥FG且EH＝FG，∴四边形EFGH是平行四边形，B项正确；A，C项显然错误；EF∥AB且EF＝12AB，∴△ABO的面积是△EFO的面积的4倍，D错误．故选B.首页课件目录末页3．[2019·郴州]如图，在▱ABCD中，点E是边AD的中点，连接CE并延长CE交BA的延长线于点F，连接AC，DF.求证：四边形ACDF是平行四边形．证明：∵ABCD是平行四边形，∴AB∥CD，即AF∥CD.∴∠AFE＝∠DCE.首页课件目录末页∵点E是边AD的中点，∴AE＝DE.又∵∠AEF＝∠DEC，∴△AEF≌△DEC(AAS)，∴AF＝DC.∴四边形ACDF是平行四边形．首页课件目录末页归类探究类型之一平行四边形的性质[2019·原创]如图，在▱ABCD中，AC是对角线，BE⊥AC，DF⊥AC，垂足分别为点E，F.求证：AE＝CF.证明：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD.∴∠BAE＝∠DCF.又∵BE⊥AC，DF⊥AC，∴∠AEB＝∠CFD＝90°.首页课件目录末页在△ABE与△CDF中，∠AEB＝∠CFD，∠BAE＝∠DCF，AB＝CD，∴△ABE≌△CDF(AAS)．∴AE＝CF.首页课件目录末页【点悟】平行四边形的对边平行且相等，对角相等，邻角互补，对角线互相平分，关于对角线的交点成中心对称等性质为我们解决有关问题提供了直接依据，熟记这些性质对解题尤为重要．首页课件目录末页1．[2019·广安]如图，点E是▱ABCD的CD边的中点，AE与BC的延长线交于点F，CF＝3，CE＝2，求▱ABCD的周长．解：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠DAE＝∠F，∠D＝∠ECF.又∵ED＝EC，∴△ADE≌△FCE(AAS)．首页课件目录末页∴AD＝CF＝3，DE＝CE＝2.∴DC＝4.∴C▱ABCD＝2(AD＋DC)＝14.首页课件目录末页类型之二平行四边形的判定[2019·原创]如图，B，E，C，F在一条直线上，已知AB∥DE，AC∥DF，BE＝CF，连接AD.求证：四边形ABED是平行四边形．证明：∵AB∥DE，∴∠B＝∠DEF.∵AC∥DF，∴∠ACB＝∠F.∵BE＝CF，∴BE＋CE＝CF＋CE，即BC＝EF.首页课件目录末页在△ABC和△DEF中，∠B＝∠DEF，BC＝EF，∠ACB＝∠F，∴△ABC≌△DEF(ASA)．∴AB＝DE.又∵AB∥DE，∴四边形ABED是平行四边形．首页课件目录末页2．如图，在△ABC中，∠ACB＝90°，∠CAB＝30°，以线段AB为边向外作等边三角形ABD，点E是线段AB的中点，连接CE并延长，交线段AD于点F.(1)求证：四边形BCFD为平行四边形；(2)若AB＝6，求四边形BCFD的面积．首页课件目录末页(1)证明：在△ABC中，∠ACB＝90°，∠CAB＝30°，∴∠ABC＝60°.在等边三角形ABD中，∠BAD＝60°，∴∠BAD＝∠ABC.∴BC∥AD.∵E为AB的中点，∴AE＝BE＝CE.首页课件目录末页又∵∠ABC＝60°，∠ABD＝60°，∴∠BCE＝60°，∠CBD＝∠ABC＋∠ABD＝120°.∴∠BCE＋∠CBD＝180°.∴BD∥CF.∴四边形BCFD是平行四边形．首页课件目录末页(2)解：在Rt△ABC中，∵∠BAC＝30°，AB＝6，∴BC＝12AB＝3，AC＝32AB＝33.∴S▱BCFD＝BC·AC＝3×33＝93.【点悟】证明一个四边形是平行四边形，有多种证明思路，我们必须注意分析，通过比较，选择最简便的证明方法．首页课件目录末页类型之三平行四边形的开放题与探究题[2019·原创]如图，四边形ABCD的对角线AC与BD交于点O，给出下列四个论断：首页课件目录末页①OA＝OC；②AB＝CD；③∠BAD＝∠DCB；④AD∥BC.请你从中选择两个论断作为条件，以“四边形ABCD为平行四边形”作为结论，完成下列各题：(1)构造一个真命题，并给出证明；(2)构造一个假命题，举反例加以说明．首页课件目录末页【解析】如果①②作为条件，那么这些线段所在的两个三角形满足的条件是SSA，不一定全等，那么就不能得到相等的对边平行；如果②③作为条件，和①②的情况相同；如果①④作为条件，由对边平行可得到两对内错角相等，那么AD，BC所在的△AOD与△COB全等，即得到平行的对边也相等，那么四边形ABCD是平行四边形；最易举出反例的是②④，它有可能是等腰梯形．首页课件目录末页解：(1)①④作为条件时：∵AD∥BC，∴∠DAO＝∠BCO，∠ADO＝∠CBO.又∵OA＝OC，∴△AOD≌△COB(AAS)．∴AD＝CB.又∵AD∥BC，∴四边形ABCD为平行四边形．(2)②④作为条件时，此时一组对边平行，另一组对边相等，可能是等腰梯形．首页课件目录末页3．[2019·常州]如图，把平行四边形纸片ABCD沿对角线BD折叠，点C落在点C′处，BC′与AD相交于点E.(1)连接AC′，则AC′与BD的位置关系是；(2)EB与ED相等吗？证明你的结论．AC′∥BD首页课件目录末页解：(2)EB＝ED.证明如下：由折叠可知∠CBD＝∠EBD.∵四边形ABCD是平行四边形，∴AD∥BC.∴∠CBD＝∠EDB.∴∠EBD＝∠EDB.∴EB＝ED.首页课件目录末页课时作业(70分)一、选择题(每题5分，共25分)1．[2019·原创]如图，在▱ABCD中，已知AC＝4cm，若△ACD的周长为13cm，则▱ABCD的周长为()DA．26cmB.24cmC．20cmD.18cm首页课件目录末页2．[2019·泸州]四边形ABCD的对角线AC与BD相交于点O，下列四组条件中，一定能判定四边形ABCD为平行四边形的是()A．AD∥BCB.OA＝OC，OB＝ODC．AD∥BC，AB＝DCD.AC⊥BD【解析】∵OA＝OC，OB＝OD，∴四边形ABCD是平行四边形．故选B.B首页课件目录末页3．[2019·遂宁]如图，在▱ABCD中，对角线AC，BD相交于点O，OE⊥BD交AD于点E，连接BE，若四边形ABCD的周长为28，则△ABE的周长为()A．28B.24C．21D.14D【解析】∵平行四边形的对角线互相平分，OE⊥BD，∴OE垂直平分BD，∴BE＝DE.∴△ABE的周长等于AB＋AD，即▱ABCD周长的一半，∴△ABE的周长为14.故选D.首页课件目录末页4．[2019·海南]如图，在▱ABCD中，将△ADC沿AC折叠后，点D恰好落在DC的延长线上的点E处，若∠B＝60°，AB＝3，则△ADE的周长为()CA．12B.15C．18D.21首页课件目录末页【解析】∵折叠后点D恰好落在DC的延长线上的点E处，∴AC⊥DE，EC＝CD＝AB＝3，∴ED＝6.∵∠B＝60°，∴∠D＝60°，∴△ADE为等边三角形．∴C△ADE＝3ED＝18.故选C.首页课件目录末页5．[2019·威海]如图，E是▱ABCD边AD延长线上的一点，连接BE，CE，BD，BE交CD于点F.添加以下条件，不能判定四边形BCED为平行四边形的是()A．∠ABD＝∠DCEB.DF＝CFC．∠AEB＝∠BCDD.∠AEC＝∠CBDC首页课件目录末页【解析】根据平行四边形的性质，得AD∥BC，AB∥CD，∴DE∥BC，∠ABD＝∠CDB，若添加∠ABD＝∠DCE，可得∠CDB＝∠DCE，从而可得BD∥CE，∴四边形BCED为平行四边形，A不符合题意；根据平行线的性质，得∠DEF＝∠CBF，若添加DF＝CF，由于∠EFD＝∠BFC，故△DEF≌△CBF，∴EF＝BF，∴四边形BCED为平行四边形，B不符合题意；根据平行线的性质，得∠AEB＝∠CBF，若添加∠AEB＝∠BCD，易得∠CBF＝∠BCD，求得CF＝BF，同理，EF＝DF，不能判定四边形BCED为平行四边形，C符合题意；根据平行线的性质，得∠DEC＋∠BCE＝180°，若添加∠AEC＝∠CBD，则得∠BCE＋∠CBD＝180°，∴DB∥CE，∴四边形BCED为平行四边形，D不符合题意．故选C.首页课件目录末页二、填空题(每题5分，共25分)6．[2018·常州]如图，在▱ABCD中，∠A＝70°，DC＝DB，则∠CDB＝.40°【解析】∵四边形ABCD是平行四边形，∴∠C＝∠A＝70°.∵DC＝DB，∴∠DBC＝∠C＝70°.∴∠CDB＝180°－70°－70°＝40°.首页课件目录末页7．[2019·达州]如图，▱ABCD的对角线AC，BD相交于点O，点E是AB的中点，△BEO的周长是8，则△BCD的周长为.16首页课件目录末页【解析】由O是▱ABCD的对角线AC，BD的交点，点E是AB的中点，可得OE＝12AD，BE＝12AB，BO＝12BD，可得△BEO的周长是△BAD周长的一半，而△BCD的周长和△BAD的周长相等，即△BCD的周长为16.首页课件目录末页8．[2019·梧州]如图，在▱ABCD中，∠ADC＝119°，BE⊥DC于点E，DF⊥BC于点F，BE与DF交于点H，则∠BHF＝度．61【解析】∵四边形ABCD是平行四边形，∴AD∥BC，DC∥AB.∵∠ADC＝119°，DF⊥BC，∴∠ADF＝90°，首页课件目录末页则∠EDH＝29°.∵BE⊥DC，∴∠DEH＝90°，∴∠DHE＝90°－29°＝61°.∴∠BHF＝∠DHE＝61°.首页课件目录末页9．[2019·龙东地区]如图，在四边形ABCD中，AD＝BC，在不添加任何辅助线的情况下，请你添加一个条件，使四边形ABCD是平行四边形．答案不唯一，AD∥BC或AB＝CD或∠A＋∠B＝180°等【解析】根据平行四边形的判定方法填上一个合适的条件即可．首页课件目录末页10．[2018·临沂]如图，在▱ABCD中，AB＝10，AD＝6，AC⊥BC，则BD＝_____.413【解析】∵AD＝6，∴BC＝6.∵AB＝10，AC⊥BC，∴AC＝AB2－BC2＝8.∴OC＝12AC＝4.在Rt△BOC中，BO＝BC2＋OC2＝213，∴BD＝2BO＝413.首页课件目录末页三、解答题(共20分)11．(10分)[2019·原创]如图，在▱ABCD中，对角线AC，BD相交于点O，过点O的直线分别交AD，BC于点E，F.求证：AE＝CF.首页课件目录末页证明：∵对角线AC，BD相交于点O，∴AO＝CO.∵AD∥BC，∴∠EAO＝∠FCO.在△AOE与△COF中，首页课件目录末页∠EAO＝∠FCO，AO＝CO，∠AOE＝∠COF，∴△AOE≌△COF(ASA)．∴AE＝CF.首页课件目录末页12．(10分)[2019·淮安]如图，在▱ABCD中，点E，F分别是边AD，BC的中点．求证：BE＝DF.证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC.∵点E，F分别是边AD，BC的中点，∴DE∥BF，DE＝BF，∴四边形BFDE是平行四边形，∴BE＝DF.首页课件目录末页(20分)13．(10分)[2019·本溪]如图，在四边形ABCD中，AB∥CD，AD⊥CD，∠B＝45°，延长CD到点E，使DE＝DA，连接AE.(1)求证：AE＝BC；(2)若AB＝3，CD＝1，求四边形ABCE的面积．首页课件目录末页(1)证明：∵AD⊥CD，AB∥CD，∴∠ADE＝∠DAB＝90°，AB∥CE.∵AD＝DE，∴∠E＝∠DAE＝45°，∴∠E＝∠B＝45°.∴四边形ABCE是平行四边形，∴AE＝BC.首页课件目录末页(2)解：由(1)知AB＝CE.∵CD＝1，AB＝3，∴DE＝2.∵AD＝DE，∴AD＝2，∴S四边形ABCE＝3×2＝6.首页课件目录末页14．(10分)[2019·张家界]如图，在▱ABCD中，连接对角线AC，延长AB至点E，使BE＝AB，连接DE，分别交BC，AC交于点F，G.(1)求证：BF＝CF；(2)若BC＝6，DG＝4，求FG的长．首页课件目录末页(1)证明：∵四边形ABCD是平行四边形，∴AE∥CD，AB＝CD，∴∠EBF＝∠DCF，∠BEF＝∠CDF.∵AB＝BE，∴BE＝CD，∴△BEF≌△CDF(ASA)，∴BF＝CF.首页课件目录末页(2)解：在▱ABCD中，AD＝BC，∵BC＝6，BF＝CF，∴CF＝12BC＝3，AD＝6.∵AD∥BC，∴△ADG∽△CFG，∴CFAD＝FGDG，即36＝FG4，FG＝2.首页课件目录末页(10分)15．(10分)[2019·荆门]如图，已知▱ABCD中，AB＝5，BC＝3，AC＝213.(1)求▱ABCD的面积；(2)求证：BD⊥BC.首页课件目录末页(1)解：如答图，过点C作CE⊥AB交AB的延长线于点E.设BE＝x，CE＝h.在Rt△CEB中，x2＋h2＝9，①在Rt△CEA中，(5＋x)2＋h2＝(213)2，②联立①②解得x＝95，h＝125.∴S▱ABCD＝AB·h＝12.首页课件目录末页(2)证明：如答图，过点D作DF⊥AB，垂足为点F.∴∠DFA＝∠CEB＝90°.∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC.∴∠DAF＝∠CBE.∴△ADF≌△BCE(AAS)．首页课件目录末页∴AF＝BE＝95，BF＝5－95＝165，DF＝CE＝125.在Rt△DFB中，BD2＝DF2＋BF2＝1252＋1652＝16.∴BD＝4.∵BC＝3，DC＝5，∴CD2＝DB2＋BC2.∴△BCD为Rt△BCD，且∠DBC＝90°.∴BD⊥BC.