课题学习-最短路径问题-【高效课堂】2022-2023学年八年级数学上学期同步精品课件(人教版)

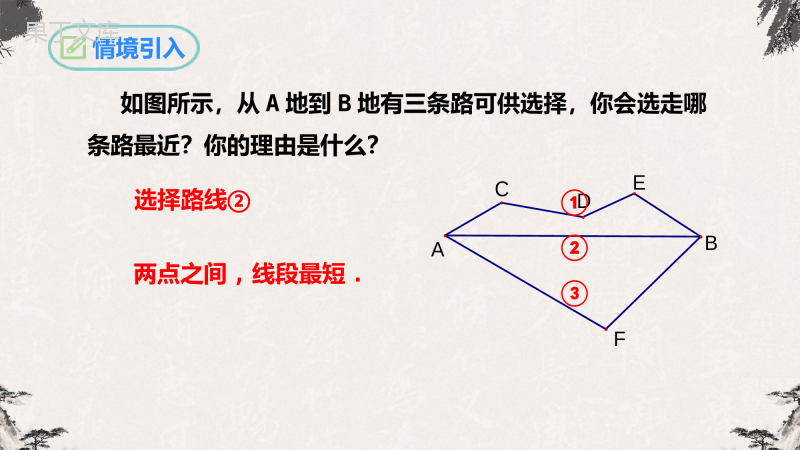
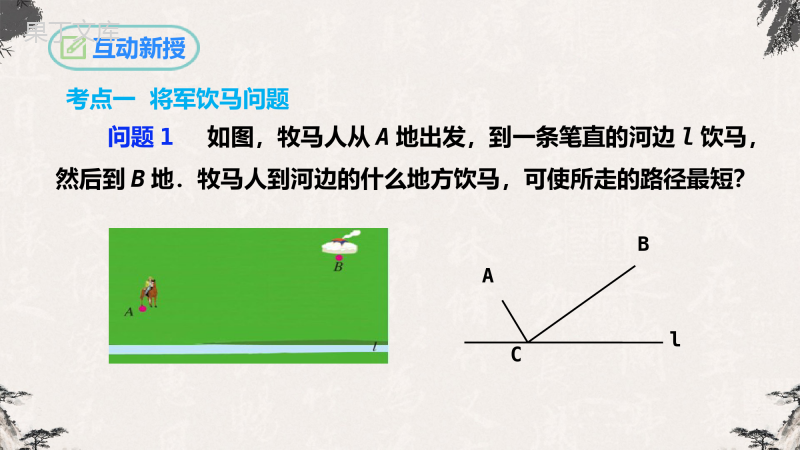
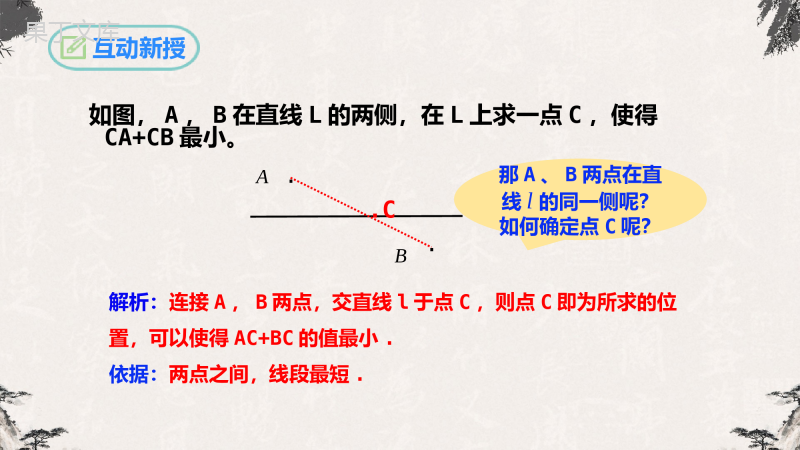
第13.4课题学习—最短路径问题人教版数学八年级上册学习目标1.利用轴对称解决简单的最短路径问题.2.能够利用轴对称、平移变换解决简单的最短路径问题，体会图形的变化在解决最值问题中的作用，感悟转化思想．情境引入如图所示，从A地到B地有三条路可供选择，你会选走哪条路最近？你的理由是什么？两点之间,线段最短.FEDCBA①②③选择路线②互动新授问题1如图，牧马人从A地出发，到一条笔直的河边l饮马，然后到B地．牧马人到河边的什么地方饮马，可使所走的路径最短？BAlC考点一将军饮马问题如图，A，B在直线L的两侧，在L上求一点C，使得CA+CB最小。互动新授∙∙ABl解析：连接A，B两点，交直线l于点C，则点C即为所求的位置，可以使得AC+BC的值最小.依据：两点之间，线段最短..C那A、B两点在直线l的同一侧呢？如何确定点C呢？∙∙ABl互动新授你能利用两点分别在直线两侧的解题思路，来解决两点在直线同一侧的问题吗？分析：如果我们能够把点B转移到直线l的另外一侧B′，同时使得对直线上任意一点C，满足BC=B′C，就可以将问题转化为“两点分别在直线两侧的情况”.那么在直线l上使得满足BC=B′C的点应该怎么找呢？如图，作出点B关于直线l的对称点B′，利用轴对称的性质可知：对于直线l上的任意一点C均满足BC=B′C.此时，问题转化为：当点C在直线l的什么位置时，AB+B′C的值最小？∙B′容易得出：连接AB′交直线l于点C，则点C即为所求.∙∙ABlC∙互动新授你能证明这个结论吗？证明：在直线l上任意取一点C′（不与点C重合），连接AC′，BC′，B′C′.由轴对称的性质可得：BC=B′C，BC′=B′C′，则AC+BC=AC+B′C=AB′，AC′+BC′=AC′+B′C′.在△AB′C′中，AB′