8-5平行线的性质定理同步课件鲁教版(五四制)数学七年级下册

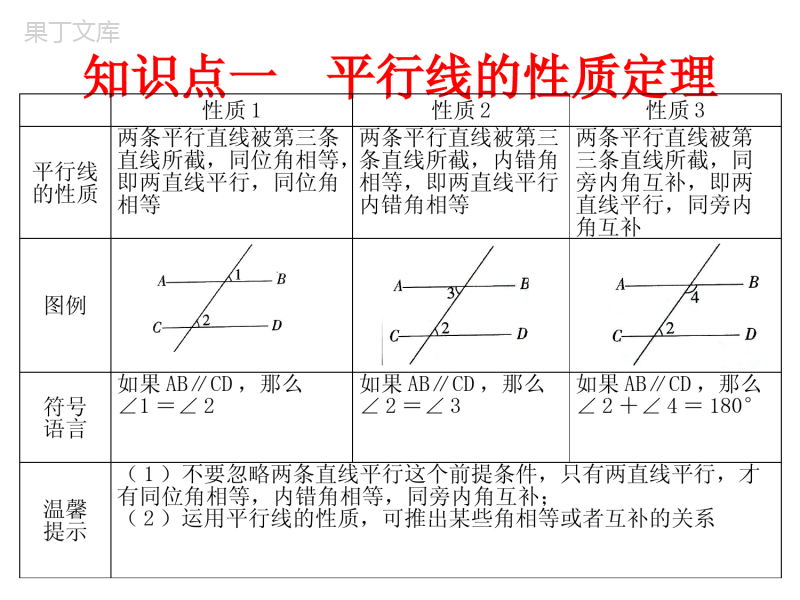
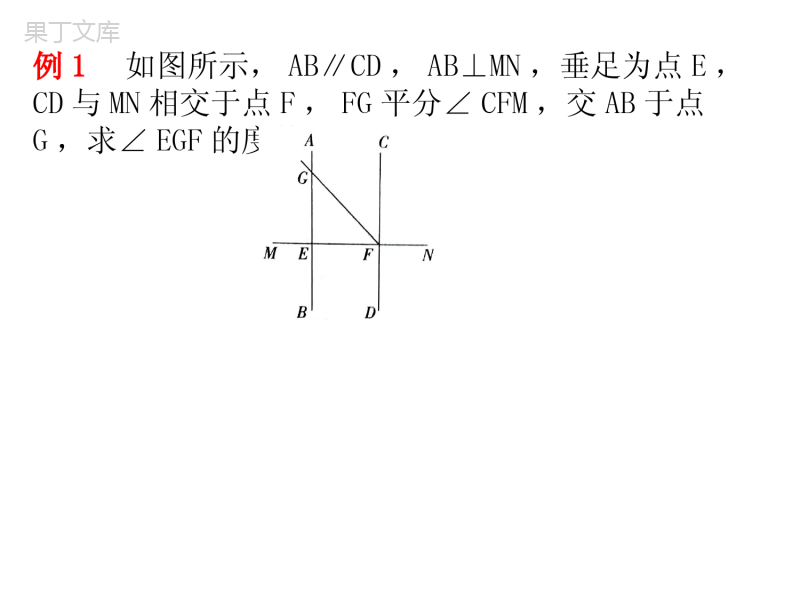
第八章平行线的有关证明5平行线的性质定理知识点一平行线的性质定理性质1性质2性质3平行线的性质图例符号语言温馨提示知识点一平行线的性质定理性质1性质2性质3平行线的性质两条平行直线被第三条直线所截，同位角相等，即两直线平行，同位角相等两条平行直线被第三条直线所截，内错角相等，即两直线平行内错角相等两条平行直线被第三条直线所截，同旁内角互补，即两直线平行，同旁内角互补图例符号语言如果AB∥CD，那么∠1＝∠2如果AB∥CD，那么∠2＝∠3如果AB∥CD，那么∠2＋∠4＝180°温馨提示（1）不要忽略两条直线平行这个前提条件，只有两直线平行，才有同位角相等，内错角相等，同旁内角互补；（2）运用平行线的性质，可推出某些角相等或者互补的关系例1如图所示，AB∥CD，AB⊥MN，垂足为点E，CD与MN相交于点F，FG平分∠CFM，交AB于点G，求∠EGF的度数.例1如图所示，AB∥CD，AB⊥MN，垂足为点E，CD与MN相交于点F，FG平分∠CFM，交AB于点G，求∠EGF的度数.解析∵AB⊥MN，垂足为点E，∴∠AEM＝90°，∵AB∥CD，∴∠CFM＝∠AEM＝90°.∵FG平分∠CFM，∴∠CFG＝∠CFM＝×90°＝45°，∵AB∥CD，∴∠EGF＝∠CFG＝45°.知识点二平行线的性质定理与判定定理的关系平行线的性质和平行线的判定正好是把条件和结论对调，它们的这种互逆关系可表示为:例2如图，∠1＝70°，∠2＝70°，∠3＝105°，求∠4的度数.例2如图，∠1＝70°，∠2＝70°，∠3＝105°，求∠4的度数.∵∠1＝70°，∠2＝70°，∴∠1＝∠2，∴a∥b，∴∠3＝∠5.又∠3＝105°，∴∠5＝105°，∴∠4＝∠5＝105°.经典例题题型一巧添平行线解题例1如图所示，已知AB∥DE，∠ABC＝80°，∠CDE＝140°，求∠BCD的度数.解析如图所示，过点C作GH∥DE，则∠DCH＋∠CDE＝180°（两直线平行，同旁内角互补）因为∠CDE＝140°（已知），所以∠DCH＝180°-∠CDE＝40°.因为AB∥DE（已知），且GH∥DE，所以AB∥GH（平行于同一条直线的两条直线互相平行）.所以∠BCH＝∠ABC＝80°（两直线平行，内错角相等）.所以∠BCD＝∠BCH-∠DCH＝40°.在有关图形的计算和推理中，常见“折线拐角”型问题，解决这类问题的方法:经过拐点作平行线，沟通已知角和未知角，从而化“未知”为“可知”这种方法应熟练掌握如“”型，要引起注意.题型二平行线的性质在折叠问题中的运用例2如图所示，将矩形ABCD沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠AGE＝32°，则∠GHC等于多少度？题型二平行线的性质在折叠问题中的运用例2如图所示，将矩形ABCD沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠AGE＝32°，则∠GHC等于多少度？∵∠AGE＝32°，∴∠DGE＝180°-32°＝148°，由折叠可得∠DGH＝∠DGE＝74°，∵AD∥BC，∴∠GHC＝180°-∠DGH＝106°.易错点在利用平行线的性质时，忽略两直线平行的条件只有在两直线平行的前提下，才存在同位角相等、内错角相等、同旁内角互补，有时无平行的条件，会因思维定式的影响而误认为同位角相等、内错角相等、同旁内角互补.易错点在利用平行线的性质时，忽略两直线平行的条件只有在两直线平行的前提下，才存在同位角相等、内错角相等、同旁内角互补，有时无平行的条件，会因思维定式的影响而误认为同位角相等、内错角相等、同旁内角互补.例如图所示，直线a，b被直线c所截，则①∠4＝∠5；②∠1＝∠2；③∠1＝∠3；④∠1＋∠4＝180°，其中结论一定正确的有（）A.1个B.2个C.3个D.4个由题图可知∠4＝∠5，∠2＝∠3，∠2＋∠4＝180°因为直线a，b不一定平行，所以∠1＝∠2，∠1＝∠3，∠1＋∠4＝180°不一定成立故只有①一定正A由题图可知∠4＝∠5，∠2＝∠3，∠2＋∠4＝180°因为直线a，b不一定平行，所以∠1＝∠2，∠1＝∠3，∠1＋∠4＝180°不一定成立故只有①一定正确.A本题易误认为a∥b，得出四个结论都正确，但题中并没有a∥b这个条件，故不能利用平行线的性质求解.